Solving Linear Systems (Graphing)
Solving Linear Systems (Substitution)
Solving Linear Systems (Elimination)
Solving Linear Systems (Word Problems)
Random Trivia
100
Solve by graphing:
y = x-2
y = -3x +2
100
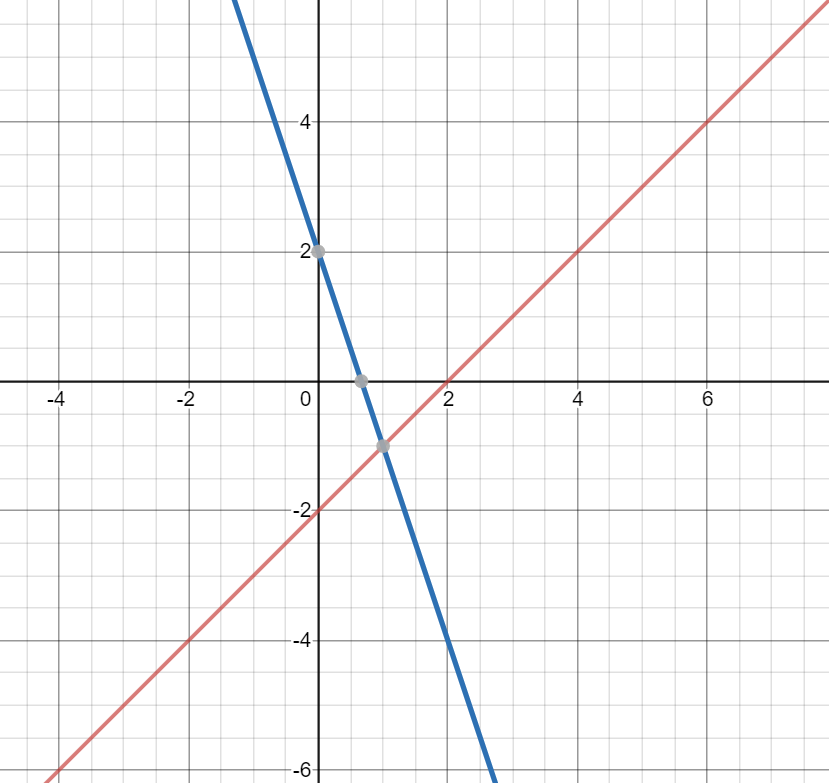
3x + y = -9
y = 5x + 7
What is (-2, -3) ?
100
-3x + 10y = 26
-4x - 3y = 2
What is (-2, 2)?
100
The sum of two numbers is 15. Their difference is 1.
What are 7 and 8?
100
Name the system with no solutions
Inconsistent System
200
Solve by graphing:
9x + 3y = 3
y = x -7
(2,-5)
200
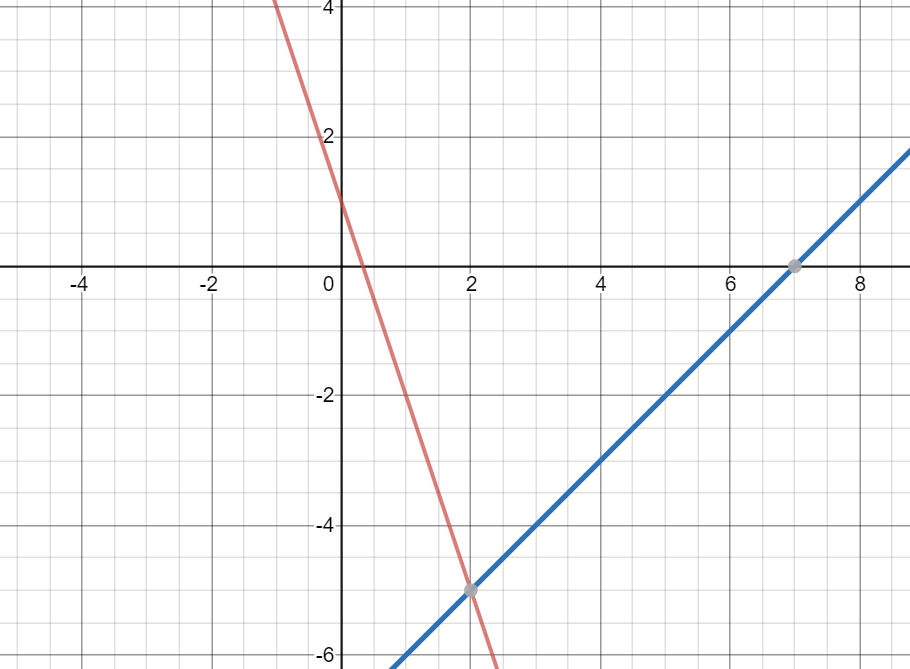
y = 2x - 7
x+ 2y = 1
What is (3, -1)?
200
-x + y = 8
x - y = -8
What are infinitely many solutions?
200
The difference between two numbers is 2. Their sum is 12.
What are 7 and 5?
200
A Consistent Dependent system has ____ Solution(s)
Infinitely Many Solutions
300
Identify a NON-SOLUTION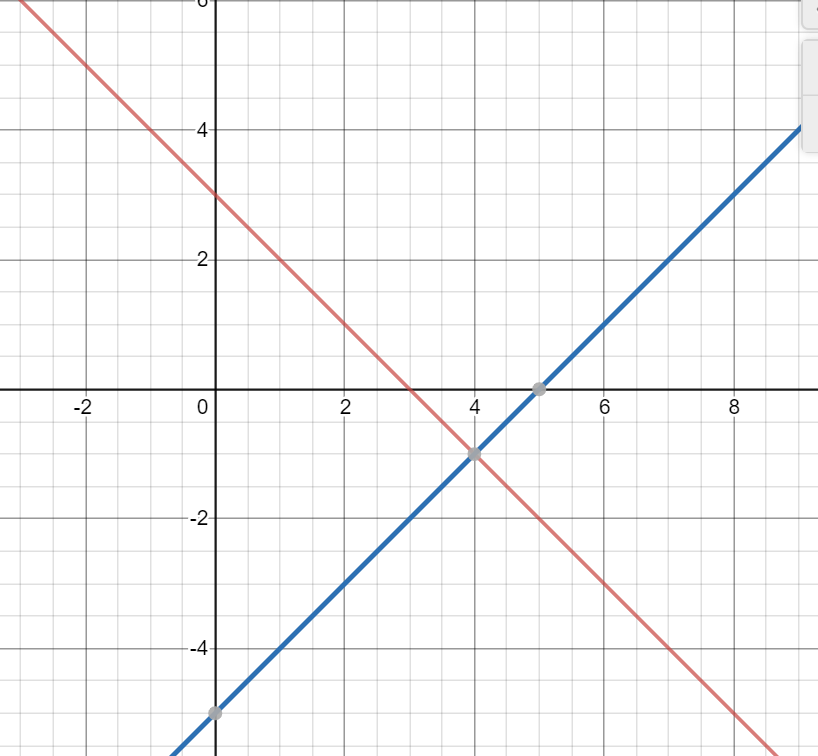
What is answers will vary, but it CANNOT be (4, -1)?
300
x + 4y = 9
x =y + 4
What is (5, 1) ?
300
5x - 3y = - 2
3x + 2y = 14
What is (2, 4)?
300
Lisa's school is selling tickets to the annual dance competition. On the first day of ticket sales the school sold 2 adult tickets and 6 student tickets for a total of $32. The school took in $67 on the second day by selling 7 adult tickets and 6 student tickets. Find the price of an adult ticket and the price of a student ticket.
What are adult tickets: $7, and student tickets: $3?
300
Plot the points, then find the intersection point
x = 3, y = -4
400
Identify the solution?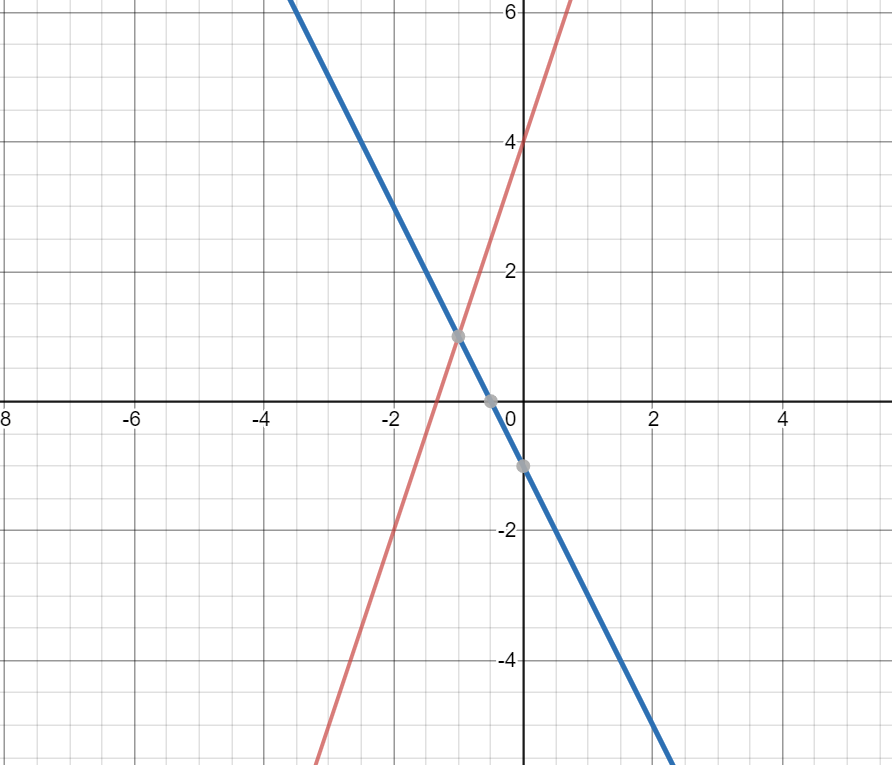
What is (- 1, 1)?
400
2x + y = -15
y = 5x + 6
What is (-3, -9) ?
400
8x + 4y = - 22
10x + 5y = - 25
What is no solution?
400
The school that Mike goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 6 senior citizen tickets and 10 student tickets for a total of $154. The school took in $140 on the second day by selling 6 senior citizen tickets and 8 student tickets. What is the price for each senior citizen ticket and one student ticket?
What are senior citizen tickets: $14, and student tickets: $7?
400
the process of Solving one equation for either variable. Then substitute the expression from the first step into the other equation. Solve the resulting equation from step 2, then substitute the solution into one of the original equations to find the other variable.
Substitution Method
500
Describe the graph and equations for a non solution system?
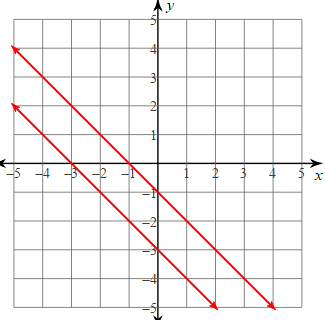
What is no solution, the slopes will be the equal, but the y-intercepts are different?
500
y = 3x + 4
y = -2x - 1
What is (-1, 1)?
500
11x -2y = - 1
-8x + 3y = 10
What is (1, 6)?
500
Joey has a handful of dimes and quarters. There are 22 coins in all. The value of the coins is $3.55. How many dimes does he have? How many quarters does he have?
What are 13 dimes and 9 quarters?
500
A system of two linear equations in two variables is an ordered pair
Solution