Name a line segment parallel to line RV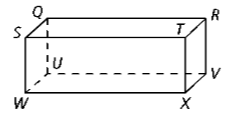
TX, SW, or QU
The angles #1 and #5 are ____?
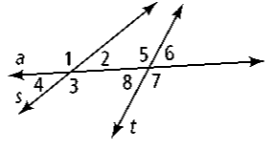
Corresponding angles
What is the angle measure of #7 and the theorem to justify it?
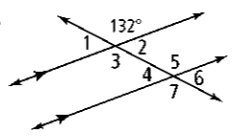
132 degrees and Alternate Exterior Angles Theorem
What is the measure of angle 1?
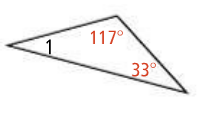
30 degrees
Find the slope of the line graphed below.
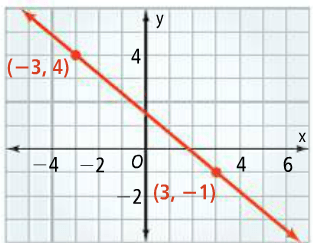
- 5/6
Name any pair of parallel planes
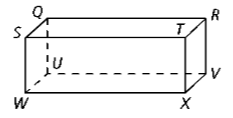
TRVX and SQUW, STXW and QRVU, or SQRT and WUVX
Angles #3 and #8 are ____?
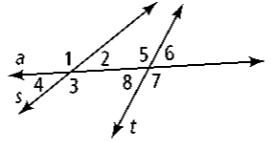
Same-side interior angles
What is the angle measure of #2 and the theorem to justify it?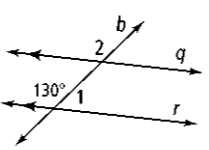
130 degrees and Corresponding Angles Theorem
What is the measure of angle 1?
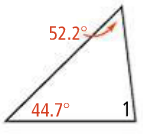
83.1 degrees
Find the slope of the line through the points
(-6, 2) and (-7, 10).
-8
Name all lines that are parallel to line WX
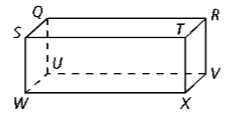
ST, QR, and UV
Angles #4 and #6 are ____?
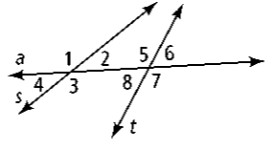
Alternate exterior angles
What is the angle measure of #2 and the theorem to justify it?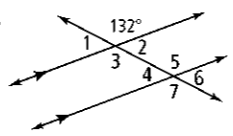
48 degrees and the Linear Pair Theorem
What is the measure of angle 1?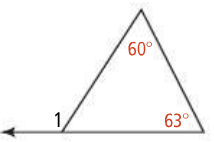
123 degrees
What is the point-slope form of an equation?
y - y1 = m(x - x1)
Name four lines that are skew (different plane) to RV.
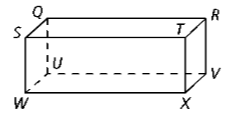
SQ, WU, WX, and ST
Name all pairs of alternate exterior angles.
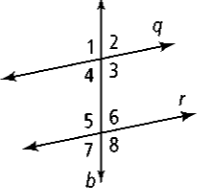
1 & 8 and 2 & 7
What is the angle measure of #1 and the theorem to justify it?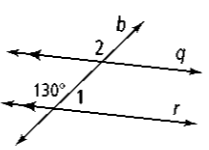
50 degrees and the Linear Pair Theorem
What is the measure of angle a?

162 degrees
What is the equation of a line with slope 3 and y-intercept 6?
y = 3x + 6
Describe a real world example of either parallel or skew lines or planes.
Ex: Two roads going parallel. The top left edge of a building and the right side of a building.
Name all pairs of corresponding angles.
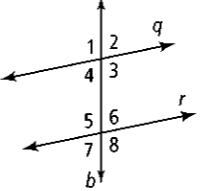
1 & 5, 2 & 6, 3 & 8, and 4 & 7
What is the measure of angle #1 and the theorem to justify it. And what is the measure of angle #2 and the theorem to justify it.
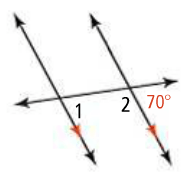
70 degrees for #1 using Corresponding Angles Theorem and 110 degrees for #2 using Same-Side Interior Angles Postulate
What is the measure of angle y?
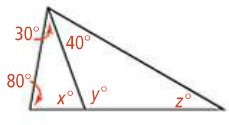
110 degrees
Find the equation of the graphed line below.
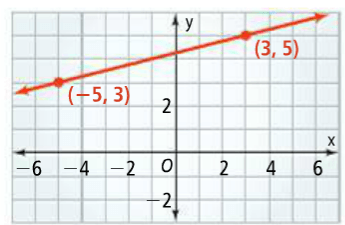
y = 1/4(x) + 17/4
or
y = 1/4(x) + 4 1/4
or
y - 3 = 1/4( x + 5 )
or
y - 5 = 1/4 (x - 3)