Solve:
5x + 7 = −3 + 3x + 22
x = 6
Is this a function? Explain how you know.
It is a function, since it passes the Vertical Line Test.
Write an equation for the line on this graph.
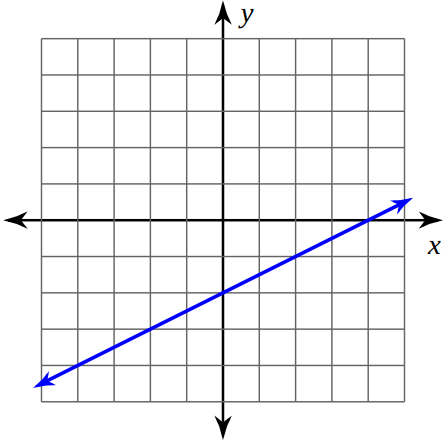
y=1/2 x-2
On a game show, you can earn y dollars completing a puzzle in x minutes. This is represented by
y=-50x+220
You earned $120 dollars. How long did it take you to complete the puzzle?
2 minutes
Is the function linear or nonlinear? Explain/show how you know.
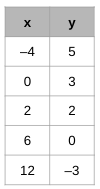
Linear. The slope is constant. The slope is -1/2.
Solve:
(x+24)/2+3=5
x=-20
Explain your answer.
A.
f(x) = 3x + 9
The equation is written in slope-intercept form, so it represents a line.
Write an equation for the line that passes through ( –1 , –2 ) and has a slope of –2.
y = -2x - 4
Write an algebraic equation for the function. Use slope-intercept form, but use t and p instead of x and y.
"The price p of an ice cream is $3.95 plus $0.85 for each topping t on the ice cream."
y = 0.85x + 3.95
p = 0.85t + 3.95
Which has a greater rate of change:
A.
y=3/4x
B. 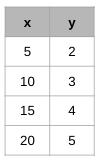
A. 3/4 is greater than 1/5
Solve:
15x-5(-2+3x)=-10
No Solution
Does the following table represent a function? If yes, add a point that makes it no longer a function. If no, specify the pairs that make it NOT a function.
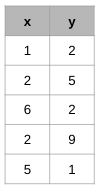
No, because the input (x) of 2 has two different outputs (y). (2, 5) and (2, 9)
A line passes through the point (2, 10) and has a y-intercept of 4. What is the equation of the line?
y = 3x + 4
Write an algebraic equation for the function. Use slope-intercept form, but use w and p instead of x and y.
"The price p of a club's membership is $30 for an enrollment fee and $12 per week w to be a member."
y = 12x + 30
p = 12w + 30
The height y (in feet) that a helicopter rises in x seconds is represented by the equation y = 7.5x.
The graph shows the height that a hot-air balloon rises. Find whether the helicopter or the hot-air balloon rises at a faster rate and justify your answer.
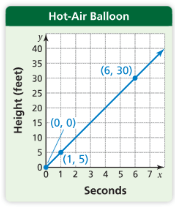
The helicopter rises faster, since 7.5 ft/s > 5 ft/s.
Where do the system of equations intersect?
2y=3x-6
y=2x-2
(-2, -6)
Is the following a function? Explain how you know.
Not a function. Does not pass the Vertical Line Test (because it would intersect at every single point!).
Only non-vertical lines are functions.
Write an equation for the line that passes through points:
( –6 , –2 ) and ( 3 , 10 )
y=4/3 x + 6
Sue’s phone costs $20 per month plus $0.10 per minute. Write an equation that represents her monthly cost y if she uses the phone for x minutes.
Explain what the slope represents.
y = 0.10x + 20
The slope, 0.10, means that for every minute Sue uses her phone, it costs an additional $0.10.
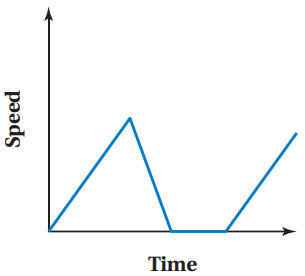
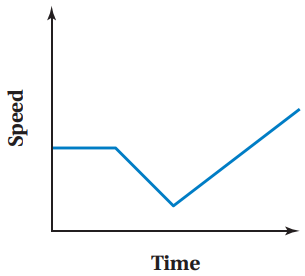
Sketch a graph that represents this situation. The horizontal axis represents "Time" and the vertical axis represents "Speed."
You ride at a constant speed, then go up a hill. Once on top of the hill, you gradually increase your speed at a constant rate.
Solve the system of equations:
2x+y=92
4x+3y=212
(32,28)
I want to add the ordered pair, (6, 5), to this table as a fifth entry. Would this make the table a function or a non-function? Explain your answer.
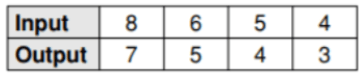
Function.
Every input would still have exactly one output.
(6,5) would appear twice in the table, but it is the same point (same input and output).
Identify the slope and the y-intercept of this line. Convert to slope-intercept form, if needed.
12 -3y = -9x
y = 3x + 4
m = 3
b: (0, 4)
The equation y = -12x + 60 represents a bathtub that is draining. The y represents the water left in the tub (in gallons), and the x represents the time that has passed since pulling the drain plug (in minutes).
Identify and interpret the slope and y-intercept.
The slope, m = -12, means that the water level in the bathtub decreases by 12 gallons per minute.
The y-intercept, b = 60, means that the bathtub started with 60 gallons of water.
Sketch a graph that represents this situation. The horizontal axis represents "Time" and the vertical axis represents "Speed."
You gradually increase your speed at a constant rate, then stop at a store for a couple of minutes. You then continue to ride, gradually increasing your speed at a constant rate.