Express Logs and Exponential Expressions
Name that graph transformation
Expanding & Condensing
Solving Exponential Equations
Solving Logarithmic Equations
100
Write the logarithm as an exponential expression:
1/2=log_49 7
49^(1/2) =7
100
The following logarithm has what transformation(s):
f(x)=log_2 (x-2)
Horizontal translation: shifts right 2
100
Expand the following logarithm:
log_6 (36x^3)
2+3log_6 x
100
Solve the following exponential equation:
8^x =12,143
x=4.5226
100
Solve the following logarithmic equation:
log_4 (3x-5)=3
x=23
200
Write the logarithm as an exponential expression:
log_3 81=y
y=4
200
The following logarithm has what transformation(s):
f(x)=-1+log_2 x
Vertical translation: shifts down 1
200
Expand the following logarithm:
ln(root(3)(x/e))
3[ln(x)-1]
200
Solve the following exponential equation:
9e^(5x)=1269
x=0.99
200
Solve the following logarithmic equation:
3+4ln(2x)=15
x=10.04
300
Write the exponential expression as a logarithm:
6^3=216
log_6 216=3
300
The following logarithm has what transformation(s):
f(x)=log_2 (-x)
Reflection: over the y-axis
300
Condense the following logarithmic expression:
1/2 ln(x)-ln(y)
ln(sqrt x/y)
300
Solve the following exponential equation:
e^(12-5x)-7=123
x=1.43
300
Solve the following logarithmic equation:
log_2 (x+3)+log_2 (x-3)=4
x=5
400
Evaluate the expression (without a calculator):
ln(1/e^2)
-2
400
The blue graph is f(x)=log(x). Identify the translations of the red graph.
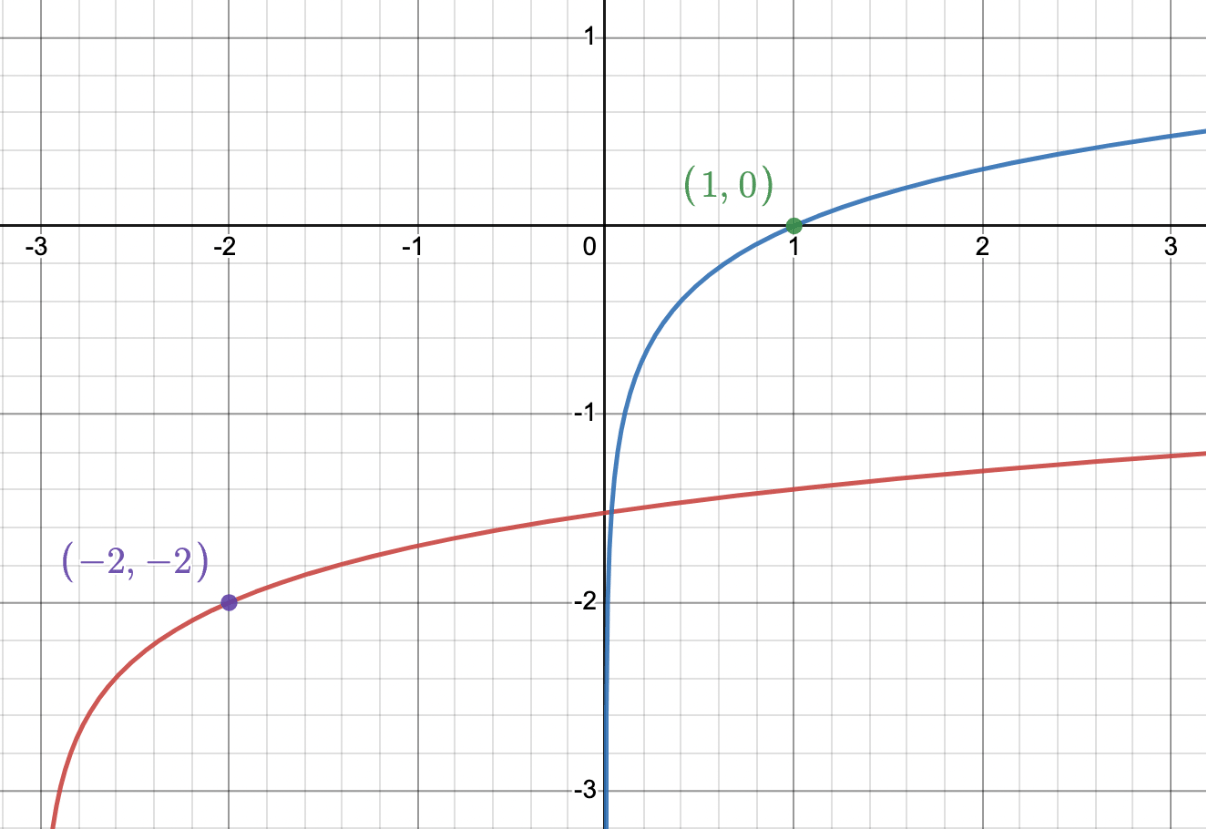
Vertical translation: down 2
Horizontal translation: left 3
400
Condense the following logarithmic expression:
4ln(x+6)-3lnx
ln((x+6)^4 /x^3 )
400
Solve the following exponential equation:
9^(x+2)=27^-x
x=-4/5
400
Solve the following logarithmic equation:
ln(x+4)-ln(x+1)=lnx
x=2
500
Evaluate the expression (without a calculator):
7^(log_7 23)
x=23
500
The blue graph is f(x)=log(x). Identify the function of the purple graph.
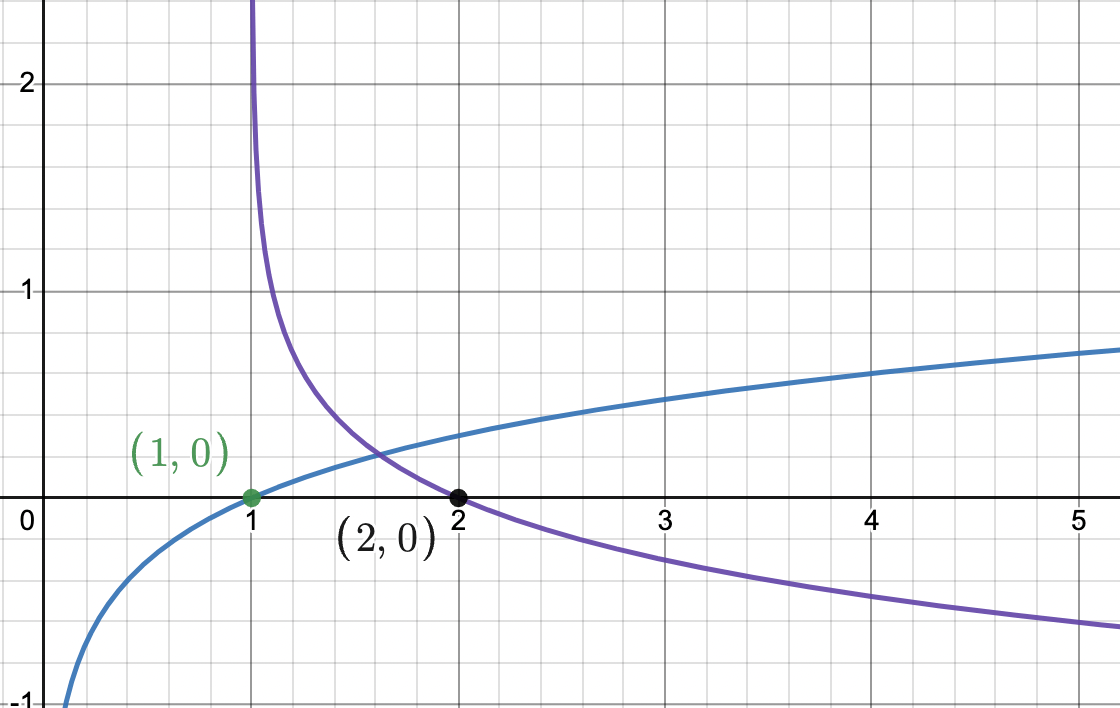
f(x)=-log(x-1)
500
Condense the following logarithmic expression:
1/3[5ln(x+5)-lnx-ln(x^2 -16)]
ln(root(3)((x+5)^5 /(x(x^2 -16)) ))
500
Solve the following exponential equation:
e^(2x)-e^x -6=0
x=1.10
500
Solve the following logarithmic equation:
log_4 (2x+1)=log_4 (x-3)+log_4 (x+5)
x=4