Domain/Range + Function Behavior
Graphing Functions
Composite Functions
Inverse Functions
Piecewise Functions
100
Identify the domain and range (use interval notation).
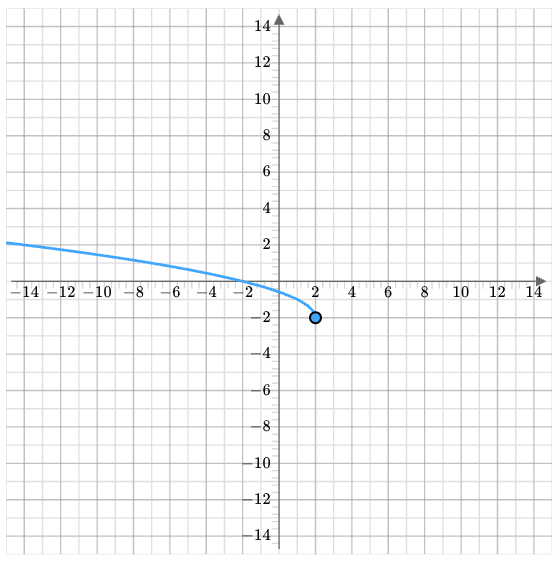
Domain:
(-oo,2]
Range:
[-2,oo)
100
Identify the parent function.
h(x) = 1/x+7
Parent Function: Rational Functions
100
Let f(x)=6x^2 and g(x)=14x+4
Find g(f(1)).
g(f(1))=88
100
Find the inverse for the following relation:
{(2,4), (4, 6), (-1, 3)}
{(4, 2), (6, 4), (3, -1)}
100
Using the graph below, complete the piecewise function by filling in the missing domain restrictions.
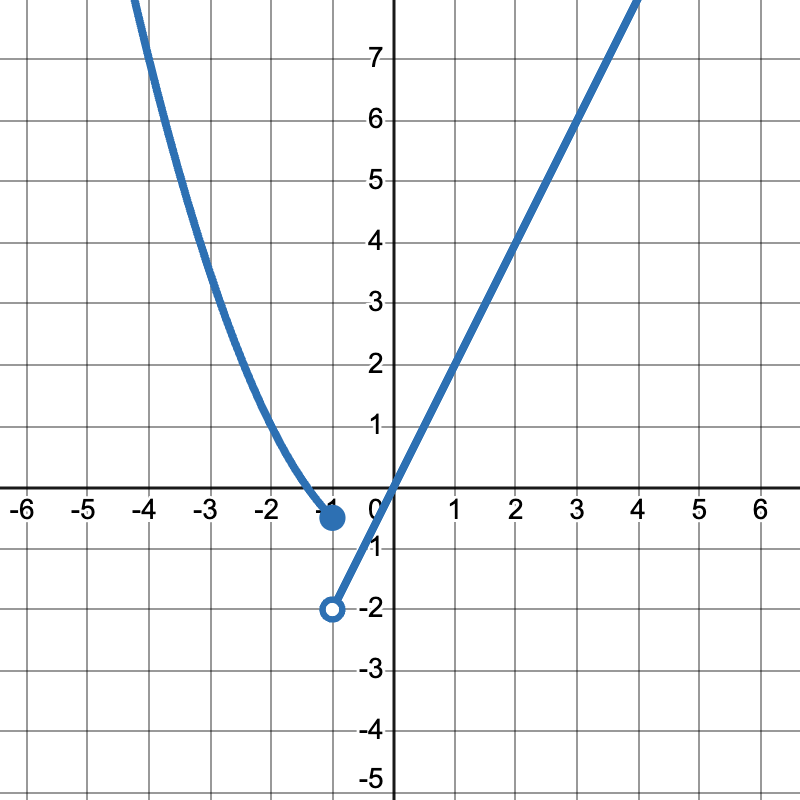
f(x)={(0.5x^2-1, ),(2x,):}
{(0.5x^2-1, x≤-1),(2x, x> -1):}
200
Identify the domain and range (use inequality notation).
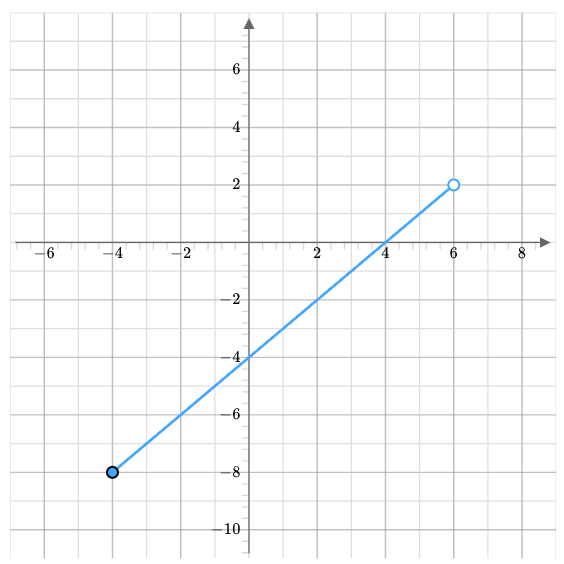
Domain: -4 ≤ x < 6
Range: -8 ≤ y < 2
200
Identify the parent function and describe the transformation.
f(x)=-|x|+2
Parent Function: Absolute Value
Description: Reflected across the x-axis and shifted up 2 units.
200
Let f(x)=6x^2 and g(x)=14x+4
Find (f∘g)(0.5).
(f∘g)(0.5) = 726
200
Find the inverse of f(x)=1/3x-2 and state the domain of f(x) and f^-1(x)
f(x)=1/3x-2
Domain of f(x): -∞ < x < ∞
f^-1(x)=3x+6
Domain of f^-1(x): -∞ < x < ∞
200
Given g(x)={(2x+17, x<-1),(-3-x,-1≤x<4),(x^3,x≥4):}
Find:
1. g(0)
2. g(-1)
3. g(5)
1. g(0) = -3
2. g(-1) = -2
3. g(5) = 125
300
Idenitfy the domain, range, and zeros of the function.
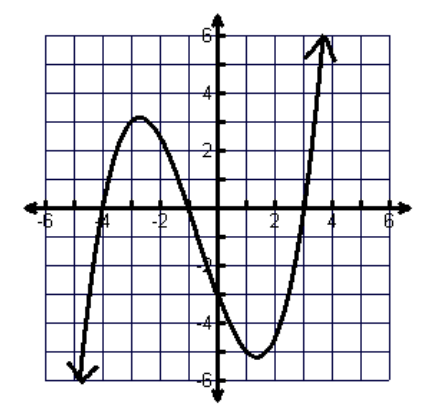
Domain: (-∞, ∞)
Range: (-∞, ∞)
Zeros: x = -4, -1, 3
300
Identify the parent function and describe the transformation.
g(x)=1/2sqrt{x+4}
Parent Function: Square Root
Description: Vertical shrink by a factor of 1/2 and shifted 4 units left
300
Let g(x)=x-2 and f(x)=4x+3
Find (f∘g)(a). Simplify if possible.
f(g(x)) = 4a-5
300
Are g(x) = 1/4x-1 and h(x)=4x+4 inverses of each other? Justify your reasoning using the inverse composition rule.
Yes they are since
g(h(x)) = x and g(g(x)) = x.
300
Graph the following function:
{(-2, x≥3),(5, x<3):}
400
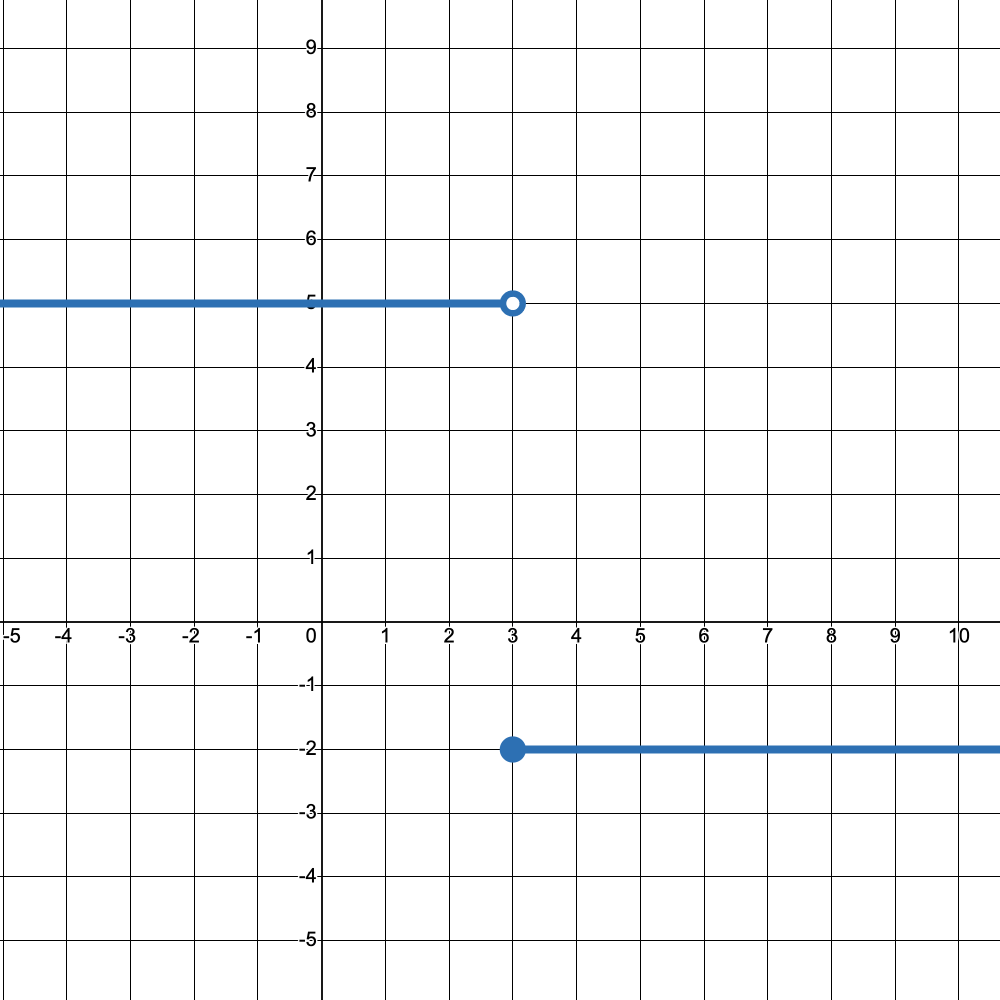
Identify the intervals for increasing, decreasing, and/or constant.
Increasing: (-∞, 4)
Decreasing: (4, ∞)
Constant: None
400
Given the parent function and a transformation description, write the equation of the transformed function.
“A quadratic function that has been shifted 5 units right and reflected across the y-axis”
f(x)=(-x-5)^2
400
Let h(x)=7/x and g(x)=-x^2.
Find g(h(b)). Simplify if possible.
g(h(b))=-49/b^2
400
Are f(x) = x^3+1 and g(x)=root(3)(x+1) inverses of each other? Justify your reasoning using the inverse composition rule
No they are not since
f(g(x)) = x+2 and g(f(x)) =root(3)(x^3+2)
400
Graph the following function:
{(x+1, x≥2),(-2x, x<1):}
500
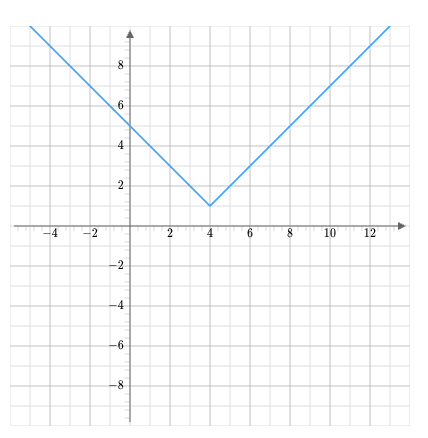
Identify the intervals for increasing, decreasing, and/or constant.
Increasing: (5, ∞)
Decreasing: (2, 5)
Constant: (-∞, 2)
500
Identify the parent function and write the equation for the transformed function.
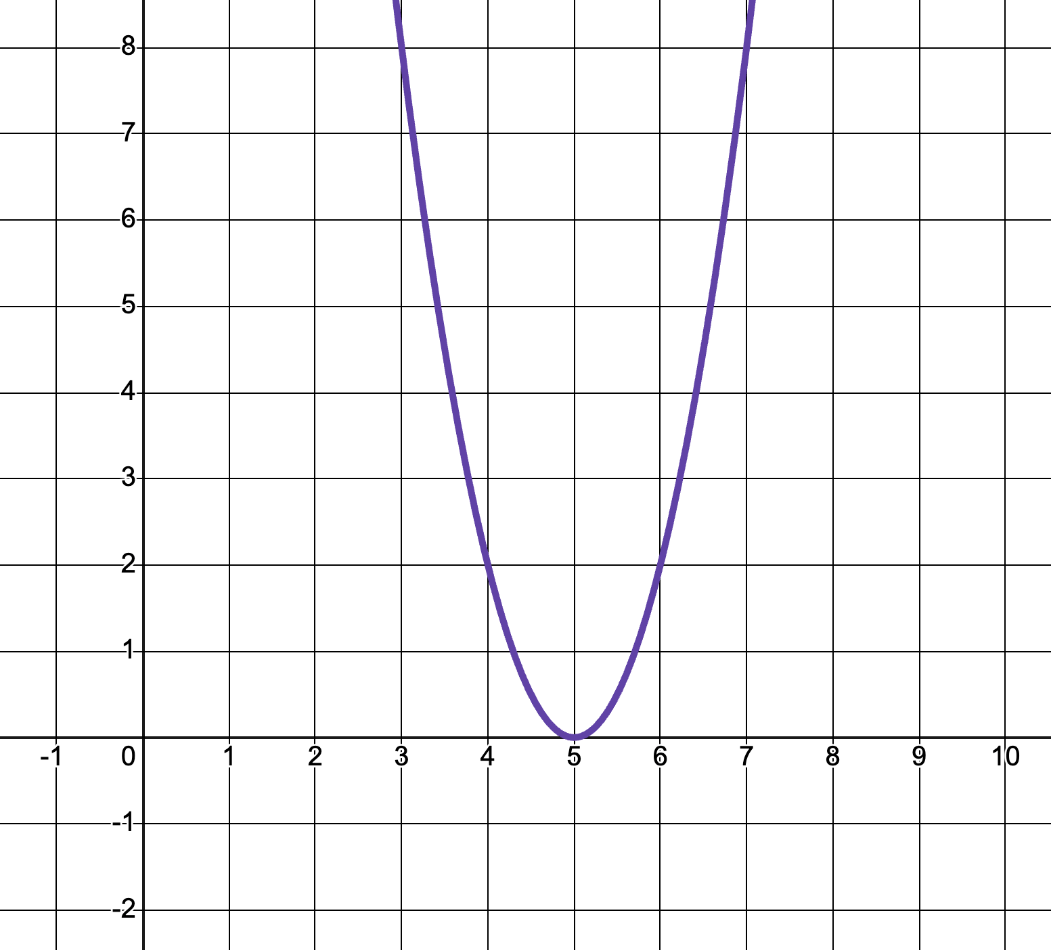
Parent Function: Quadratic
f(x) = 2(x-5)^2
500
Let h(x)=7/x, f(x)=x-2 and g(x)=-x^2.
Find f(g(h(3.5))).
f(g(h(3.5))) = -6
500
Find the inverse of f(x)=x^2+4 and state the domain of f(x) and f^-1(x)
f(x)=x^2+4
Domain: 0 ≤ x < ∞
f^-1(x)=sqrt(x-4)
Domain: 4 ≤ x ≤ ∞
500
Write an equation for the following function.
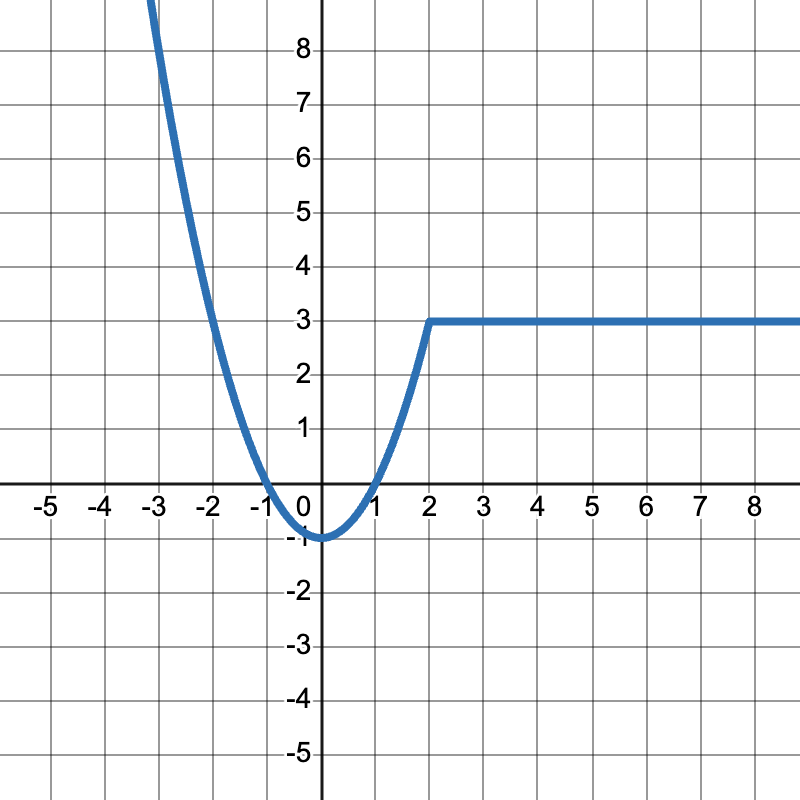
f(x)={(x^2-1,x<2),(3, x≥2):}