Proportional or Not Proportional
Reading Graphs
Equations
100
What two things does a graph need to have to be proportional?
- Goes through the origin (0,0)
- Straight line (steady/constant rate)
100
Based on the graph, what do x and y represent in this problem?
x = time (hours)
y = distance (miles traveled)
100
Write a word problem to match the table. Then write an equation to represent your word problem.
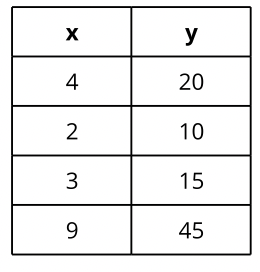
Word Problem:
Equation: y = 5x
200
Is this graph proportional? Why or why not?
Yes because it goes through the origin and is a straight line (increases at a steady/constant rate)
200
Based on the graph, how many miles are walked in 1 hour?
2 miles
200
The equation y = 0.5x can be used to determine the cost (y) in dollars per cookie.
What does the number 0.5 represent in this equation?
The cost ($) per cookie.
300
Is this graph proportional? Why or why not?
No because it does not go through the origin
300
The graph below shows the proportional relationship between gallons of gas and distance traveled. According to the graph, what is the unit rate of miles per gallon?
1 gallon = 35 miles
300
Based on the graph, what equation could be used to show the cups of peaches needed for every cup of grape juice?
y = 2/5 x
y = 0.4x
400
Does this table show a proportional relationship between number of mules and bales of hay? Why or why not?
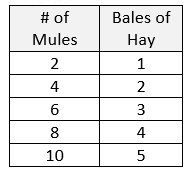
Yes because the number of mules per bale of hay stays the same (0.5 mules = 1 bale of hay)
400
Based on the graph, what is the unit rate of gallons per dollar?
0.4 gallons per dollar
400
The table below shows the proportional relationship between number of cases and rolls of paper towels.
Write an equation representing the number of rolls (r) for every case (c) they order.
r = 12x
500
Does this table show a proportional relationship?
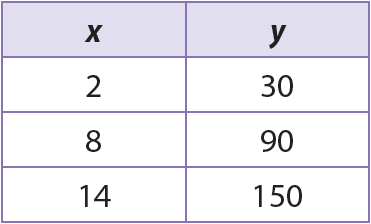
No because the constant of proportionality/rate does not stay the same.
2 to 30 = 15
8 to 90 = 11.25
14 to 150 = 10.71 (rounded)
500
The graph below shows the speed of 3 different students walking to class. All the students walked at a constant rate. Which student (A, B, or C) was walking the quickest? Explain your answer.
Student A was walking the quickest because they walked at a speed of 3m per second. Student B walked at a rate of 1m per second. Student C walked at a rate of 0.5m per second.
500
The table below shows the proportional relationship between number of children attending a party and number of liters of soda bought..
Part 1: Write an equation that represents the number of liters bought (L) for each child attending (c).
Part 2: If there are 12 liters bought, how many children are attending?
If there are 28 children attending, how many liters will be bought?
Part 1:
L = 3/4c or L = 0.75c
Part 2:
c = 16
L = 21