Exam 1
Exam 2
Exam 3
Post Exam 3
100
Given f(x):
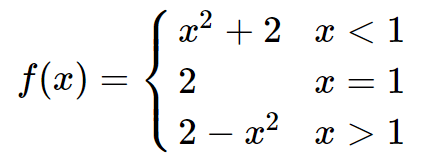
Find:
lim_(x->1^+)f(x)
1
100
Find the derivative of f(x).
f(x)=e^(7x)cos(10x)
7e^(7x)cos(10x)-10e^(7x)sin(10x)
100
Compute the sum
sum_(i=0)^4 (i^3-1)
95
100
George deposits $100 into an account that pays an annual interest of 4% continuously compounded. Rounded to the nearest year, when will he have $400 in the account?
35 years
200
Considering the graph find the following limits.
lim_(x->2)f(x)
lim_(x->-3)f(x)
DNE and 0
200
What is the slope of the tangent line to the graph at x = 1?
y=ln(2x^3+5x)
11/7
200
Given h(x)
h(x)=(2x+1)/(3x^2-x+6)
Find:
lim_(x->-oo)h(x)
0
200
Find the area of the region bounded by x=0, x=10, y=0, and
y=x^3+5
2550
300
Given the function f(x). Find the discontinuities of f(x).
f(x)=(-3x)/(x^2+6x)
f(x) has a hole at x = 0 and a vertical asymptote at x = -6.
300
What is a critical number of
y=1/5x^5+2x^4
-8
300
Evaluate
int (e^x+4x+6)\ dx
e^x+2x^2+6x+C
300
Use the Trapezoidal Rule with 4 trapezoids to estimate the area under y from x = 1 to x = 9. Round the answer to the nearest integer.
y=sqrt(3x+1)
31
400
Given f(x)
f(x)=7x^2+4x
which of the following equals
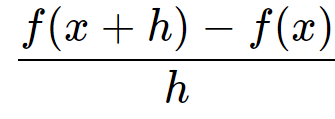
14x+7h+4
400
A spherical balloon is being inflated so that is radius is increasing at the rate of 1/4 cm/s. At what rate is the surface area of the spherical balloon increasing when the radius is 3/2 cm? The surface area of a sphere is S, where r is the radius of the sphere.
S=4pir^2
3pi (cm^2)/s
400
Given is f'(x). What intervals is f(x) INC.
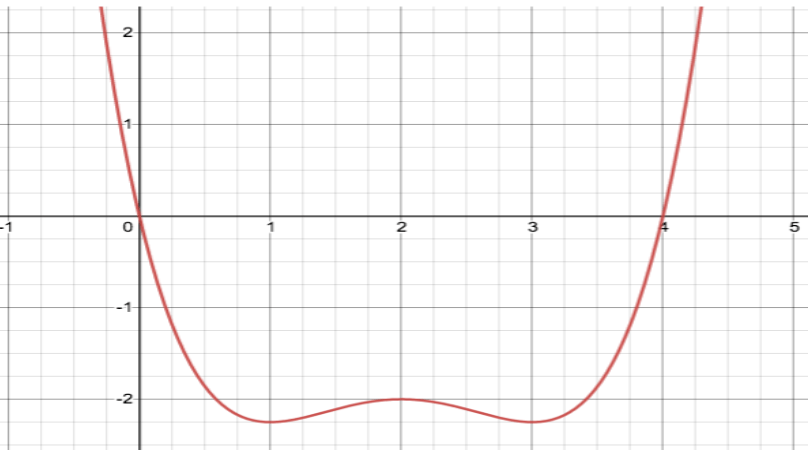
(-oo,0)(4,oo)
400
Given that the radioactive isotope Plutonium-240 has a half-life of 6563 years, what is its decay rate, k?
(ln(1/2)/6563)
500
Find the derivative:
y=x/10+9x^4-1/4sqrt(x)
1/10+36x^3-1/(8sqrtx)
500
Find the equation of the tangent line to the graph at the point (1,1).
2x^3+3y^2=5xy
y=-x+2
500
What is/are the vertical asymptotes of g(x).
g(x)=(x-1)/(x^2-4)
x = -2 and x = 2
500
Evaluate the definite integral
int_0^1 (x^2-x^3)/(2sqrtx)dx
2/35
600
Find the equation of the tangent line to f(x) at x = 2.
f(x)=3x^2-2x-1
y=10x-13
600
Find the largest open interval on which f(x) is INC.
f(x)=2/3x^3-2x^2-6x+4
(-oo,-1)(3,oo)
600
You have 20L feet of fencing to make a rectangular flower garden alongside the wall of your house, where L is a positive constant. The wall of the house bounds one side of the flower garden. What is the largest possible area for the flower garden?
50L^2ft^2
600
Supposed that the half-life of some radioactive material is 2 years. If you start with 1,024,000 pounds of this radioactive material, how long will it be until there are only 1,000 pounds left? Round your answer until the nearest year.
20 years
700
Find g'(x).
g(x)=secx+tanx
secxtanx+sec^2x
700
The derivative of a function f(x) is f'(x). Find the largest open interval on which f(x) is DEC.
f'(x)=(x-4)^2(x+3)
(-oo,-3)
700
Evaluate the indefinite integral.
int7cscx(cscx-8cotx)dx
-7cotx+56cscx+C
700
Given:
int_1^8f(x)dx=3, int_0^4f(x)dx=-7, int_0^8f(x)dx=10
Find:
int_1^4 f(x)dx
-14
800
Find the x value(s) at which y has a horizontal tangent line.
y = 4x^3e^x
x = -3 and x = 0
800
Choose the correct statement about the absolute minimum and the absolute maximum of f(x) on the interval of [0,2].
f(x)=x^4-4x
Abs MIN: (1,-3)
Abs MAX: (2,8)
800
For a cylinder with a volume of 100, find the radius which minimizes the surface area.
V = pir^2h
SA=2pirh+2pir^2
(50/pi)^(1/3)
800
The growth rate of a population is given by P'(t) where t is months after January 1, 2000. By how much did the population increase from March 1, 2000 to November 1, 2000? Round your answer to the nearest integer.
P'(t)=2e^t+t^3-7
46478
900
Given f(x). What is f'(0)?
f(x)=(sinx)/(7+x)
1/7
900
The position function for a particle moving in a straight line is given by s(t), where s is in meters and t is in seconds. Find the position of the particle when the acceleration is 2 m/sec^2.
s(t)=4t^3-23t^2+50t+6
46 m
900
A company's marketing department has determined that if their product is sold at the price of p dollars per unit then they can sell q=1000-125p units. What is the maximum possible revenue from selling this product?
2000 dollars
900
An isotope is being studied for its radioactive properties. After being contained for 2 years, it loses 8.24% of its original quantity. What is the half-life of this isotope?
About 16.12 yrs
1000
The population of a herd of cattle over time (in years) is given by p(t). What is the growth rate (in cattle per year) when t = 5 years?
p(t)=70(4+0.1t+0.01t^2)
14
1000
Find the x value at which the inflection point of g(x)
g(x)=10x^3+30x^2+20
-1
1000
Given g'(x) with g(1)=1, find g(2).
g'(x)=2/x+1/(2sqrt(x))
2ln2+sqrt(2)
1000
Radioactive plutonium has a half-life of 24110 years. What percent of a given amount remains after 1000 years? (Round your answer to two decimals places)
97.17%
1100
Given y, find y'(2).
y=(1/8x^2+x-1/x)^4
56
1100
A car drives towards a 15 ft tall post. A sensor sits at the top of the post. If the distance between the car and the sensor is decreasing at a rate of 48 ft/s when the car is 36 ft away from the base of the post, how fast is the car driving?
52 ft/s
1100
Use the right Riemann sum to estimate the (signed) area beneath the curve f(x) over the interval [0,6] with 3 rectangles.
f(x)=x^2
112
1100
The growth rate of the population of a country is given by P'(t), where t is in years and t=0 corresponds to 2010. How much did the population grow from 2010 to 2013? Round your answer to the nearest integer.
P'(t)=(t)^(1/3)(2651t+2210)
21,919 people
1200
Find the largest open interval where the function is concave DOWN.
f(x)=1/12x^4+1/3x^3+9x
(-2,0)
1200
A box with a square base and an open top must have a volume of 4000 cm^3. If the cost of the material used is $1 per cm^2, the smallest possible cost of the box is?
$1200
1200
Approximate the area of the shaded region by using the Trapezoidal Rule with n=4.
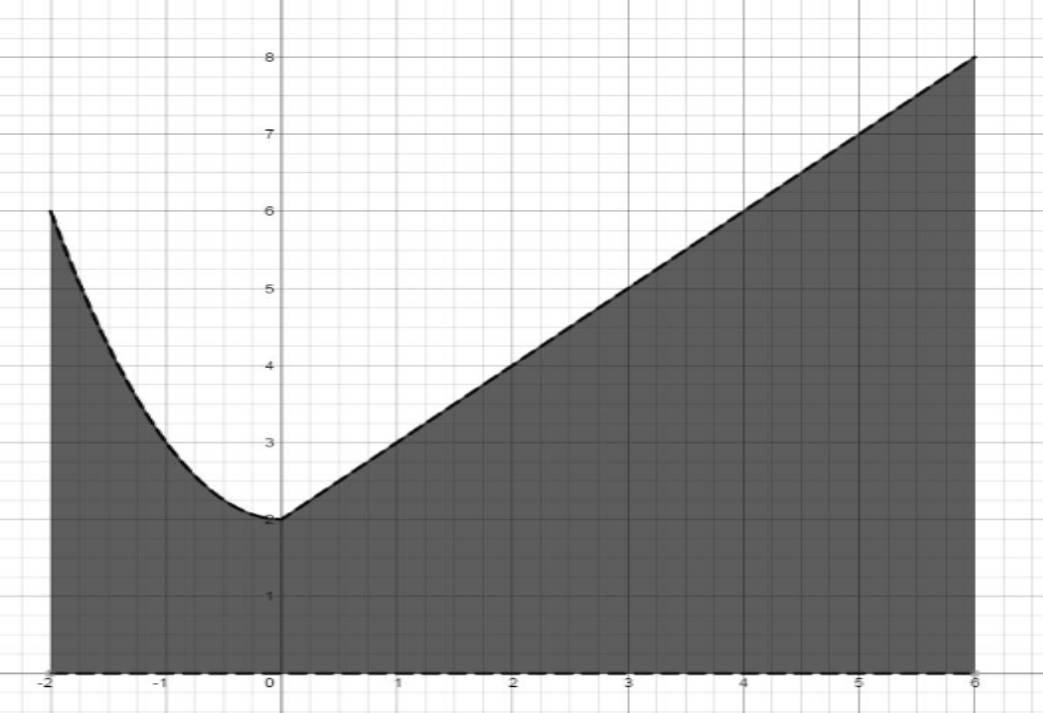
38