Tal/algebra
Procent
Geometri
Sannolikhet
Funktioner
100
förenkla uttrycket
3-6y-2(4-4y)
2y-5
100
5% av ett tal är 35 vad är det talet?
talet är 700
100
i en rätvinklig triangel med sidan a b c, vad är det förhalandena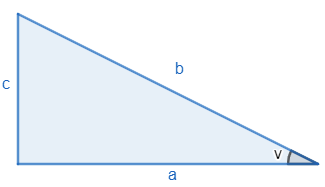 
a/b=
c/b=
c/a=
a/b=cos(v)
c/b=sin(v)
c/a=tan(v)
100
i en påse finns 5 gula, 6 röda och 14 vita kulor. Hur stor är sannoikheten att dra en gul kula?
5/25=1/5=0.20=20%
100
Vad är formeln till räta linjens ekvation?
y=kx+m
200
skriv ett uttryck där det är faktoriserat så mycket som möjligt.
3xa-6a
3a(x-2)
200
Ett av talen nedan är 25% mindre än ett av de andra talen. vilka är de två talen?
2, 4, 6, 8, 10, 12, 14
6 och 8
200
Tio kuber målas röda och sätts ihop till en trappa enlig bilden. Trappan målas blå på varje synlig yta (toppen, fram, bak och båda sidorna men inte botten) Hur många sidor är fortfarande röda?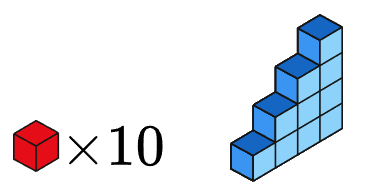
28 sidor
200
Det är 10 personer som ska ha en armbrytartävling där alla möter varandra en gång. Hur många matcher blir det?
45 st
(10*9)/2=45
200
vad är räta linjens ekvation för denna graf?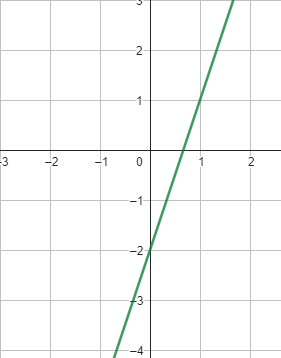
y=3x-2
300
vad är största naturliga tal som är en delare till
187; 323 och 3553
17
11*17*19=3553
17*19=323
11*17=187
300
skriv talen i storleksordning
350‰ 30% 8000ppm 0.40 3/35
8000ppm < 3/35 < 30% < 350‰ < 0.40
300
vad blir resultanten av
vec u och vec v
i kordinatform
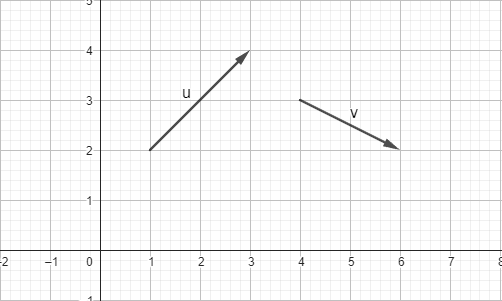
(4,1)
300
En standard kortlek med 52 kort, som har 26 röda kort och 26 svarta, blandas. är sannolikheten större än 50%, mindre än 50% eller exakt 50%?
mindre än 50%
300
f(x)=2x^2-4x+3
vad blir f(-2)
19
f(-2)=2*(-2)^2-4(-2)+3
=2*4-4*(-2)+3
=8+8+3
=19
400
lös ekvationen
(x-2)/6-(x+1)/2=3x
400
Om jag hat köpt en tavla som ökar i värde med 21% första året och har gjort en total ökning med 41% efter två år. Med hur många procent ökade tavlans värde under det andra året?
en ökning med 16.5% under det andra året 16.5%
Förändringsfaktorn andra året kan beräknas
1.41/1.21=1.165
förändringsfaktorn 1.165 innebär en ökning med 16.5% under det andra året.
400
vilken av trianglarna har arean 1
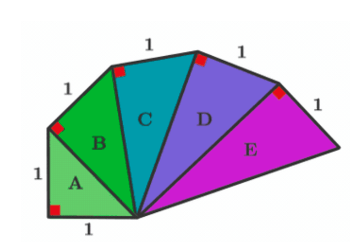
Triangel D
400
I en byrålådan finns tre par strumpor. Eva tar på måfå 2 strumpor ur lådan. hur stor är sannolikheten att de tillhör samma par?
20%
400
vilka typer av funktioner är detta
f(x)=0.05x^2
g(x)10*0.5^(x/10)
f(x) är en potensfunktion
g(x) är en exponentialfunktion
500
lös ekvationen
2^(x+1)-2^(x-1)=3
2^(x+1)-2^(x-1)=3
2^x*2^1-2^x*2^(-1)=3
2*2^x-0.5*2^x=3
1.5*2^x=3
2^x=3/1.5
2^x=2=2^1
x=1
500
På mellanstadiet är förhållandet mellan åk 5 och åk 6 är 7:10. Om det är 9 st fler som går i åk 6. Hur många är det om går i åk 5
Det är 21 st.
500
Vad är arean av den röda delen exakt
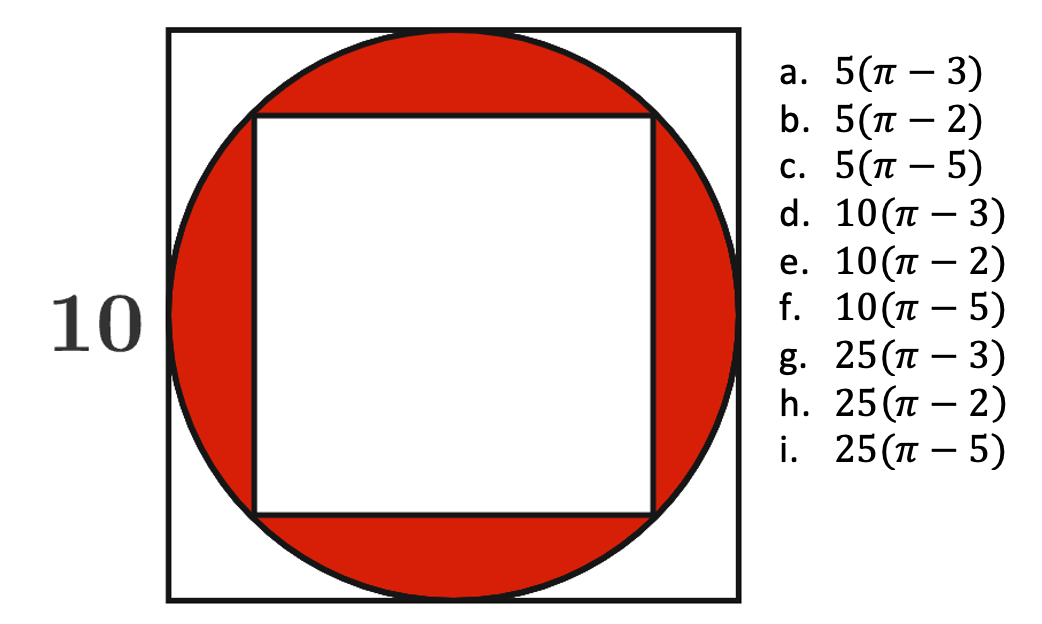
25(π-2)
500
På hur många sätt kan man ordna bokstäverna i ”KALLE” så att de två L:en inte står bredvid varandra.
36 sätt
Det finns 120 sätt att aragera de fem bokstäverna
5*4*3*2*1=120
men de två L:n spelar ingen roll vilket av dem som är på vilken platts
KaLLe är samma sak som KaLLe
det betyder att det bara finns 60 sätt att att arrangera bokstäverna eftersom vi kan dela antal sätt med 2.
sedan dår vi tänka på när de två L:n står bradvd varandra som en enskilt objekt
K, A, E, och LL
Då finns det bara 4 objekt att placera ut
4*3*2*1=24
det betyder att antal sätt att skriva utan att de två L:n står bredvid varandra är
60-24=36
500
vad är definitionsmängd och värdemängd för funktionen
f(x)=sqrt(x-2)
definitionsmängd
x>=2
värdemängd
y>=0