Average Rate of Change
Limits and Continuity
Limits and Continuity (Part 2)
Instantaneous Rate of Change and the Derivative, Tangent Lines
Miscellaneous
100
Let
f(x) = 2x - 4.
Compute the average rate of change of f(x) from x = 3 to x = 5.
2
100
Suppose f(x) is given by the following graph.
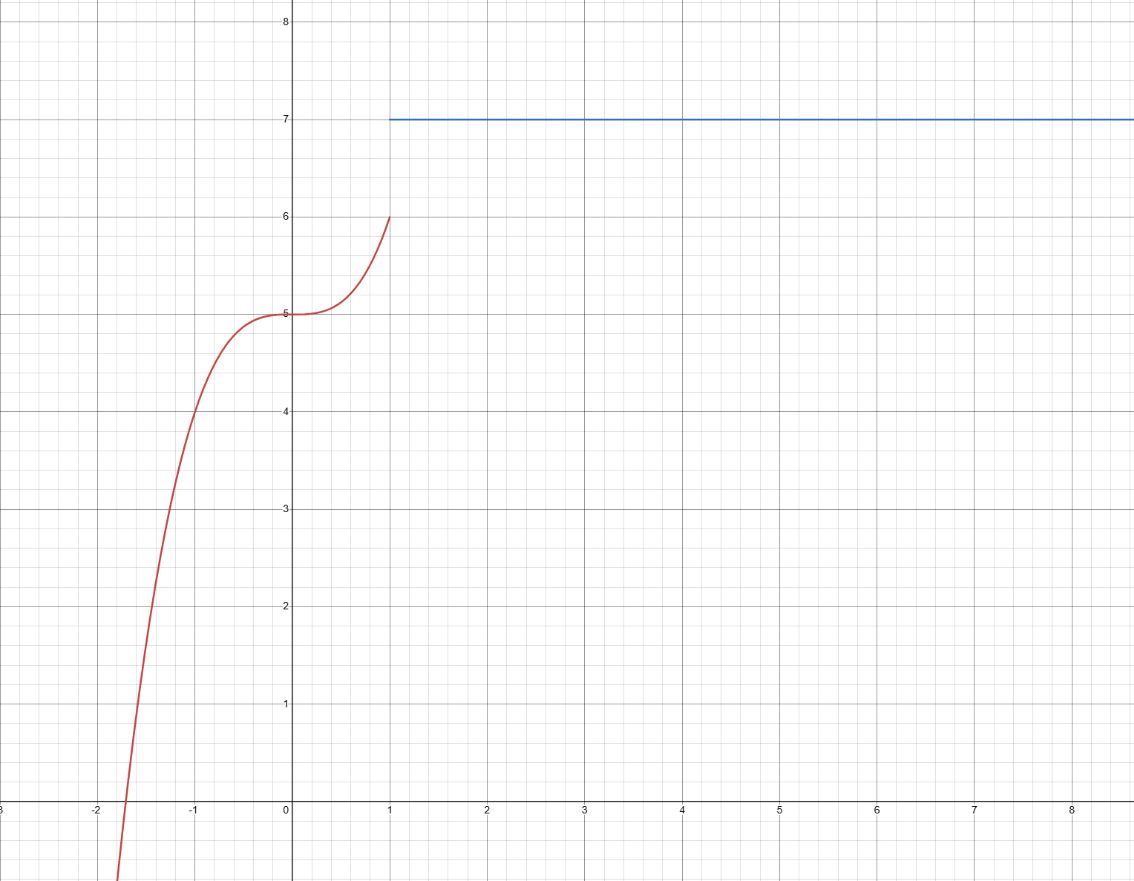
Determine
\lim_{x\to1^-}f(x).
6
100
Let f(x) be the function depicted below.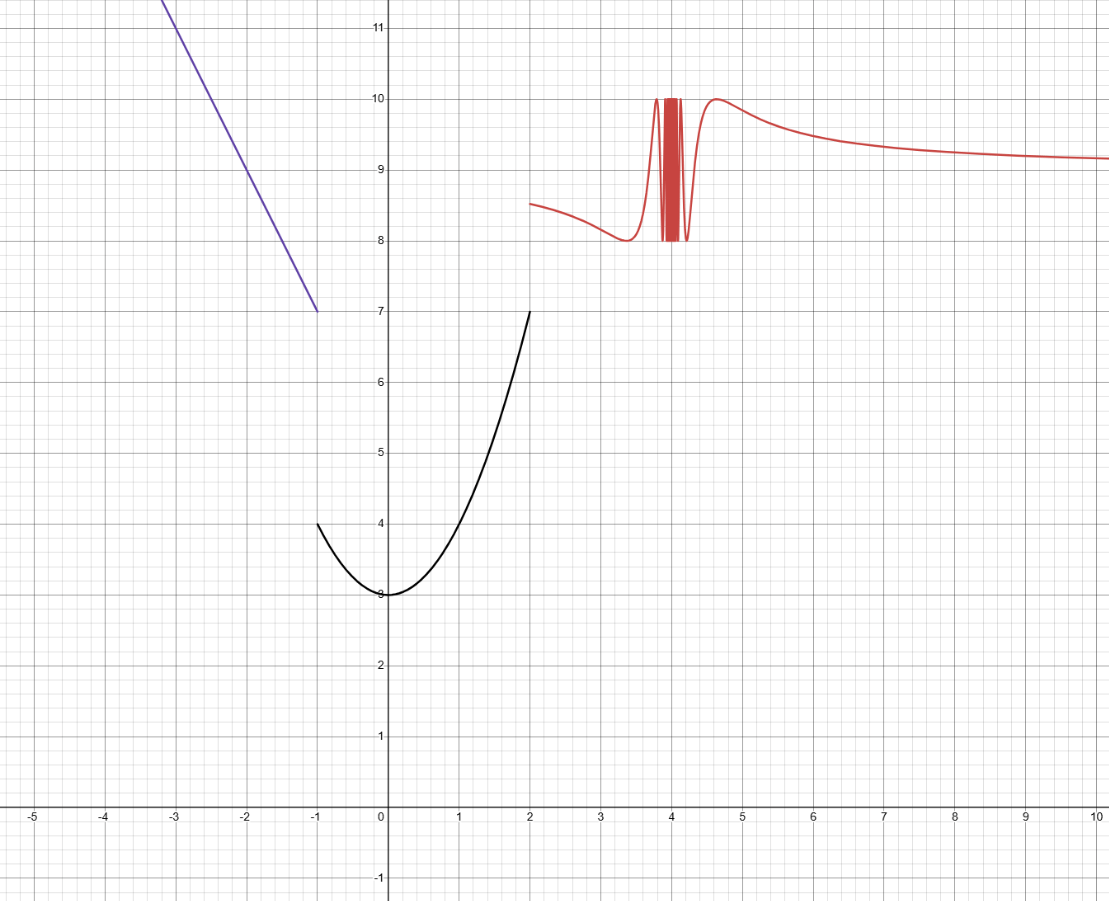
Is f(x) continuous at x = -1? At x = 0? At x = 2?
Not continuous at x = -1 or x = 2. Continuous at x = 0.
100
Suppose f(x) = x + 5. Compute the difference quotient
\frac{f(x+h)-f(x)}{h}.
Make sure that your expression can be evaluated as h approaches 0.
1
100
Suppose f(x) = mx + b, where m and b are real numbers. Compute the tangent line to f(x) at x = 351,772.
y = mx + b.
200
Suppose
f(x) = x^2+3x+6.
Compute the average rate of change of f between x = 1 and x = 4.
8
200
Consider the piecewise function f(x) given by
f(x) = {(Ax^2-6x,if x<3),(-12+Ax,if x>=3):}
Find A such that f(x) is continuous at x = 3.
A = 1
200
Consider the piecewise function f(x) given by
f(x) = {(3x^3-5x^2+14x-7,if x<1),(x^2+5,if x>=1):}
Compute
\lim_{x\to1^+}f(x).
6
200
Compute the instantaneous rate of change of
f(x) = 5x^2 + 14x - 17.
at x = 4.
54
200
The following function is differentiable except at which x values?
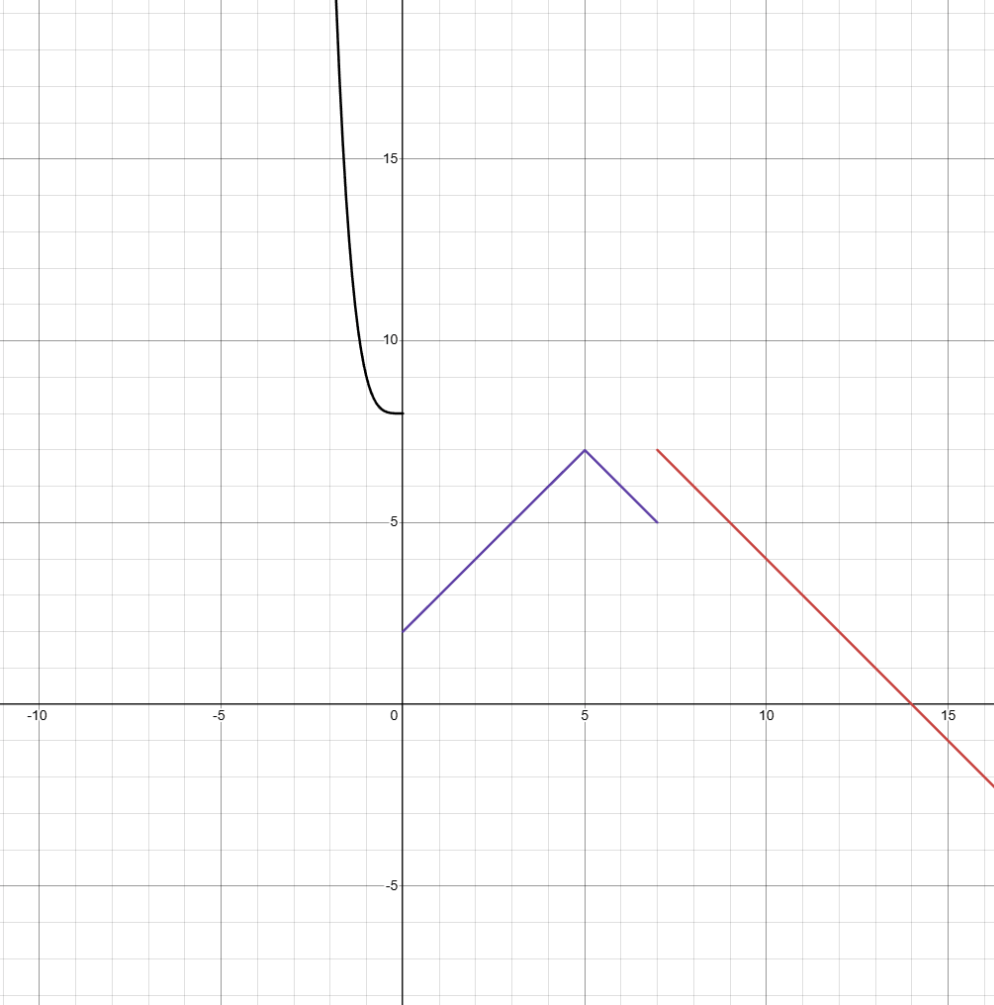
x = 0, 5, and 7.
300
Suppose a train, stationary between 1 A.M. and 9 A.M., leaves station A at 9:00 A.M. and arrives to station B at 3 P.M. Suppose further, that station A is 77 miles from station B. Compute the average speed of the train between 8 A.M. and 3 P.M.
11
300
Compute
\lim_{x\to2}\frac{x^2-4}{x^2+11x-26}.
4/15
300
Sketch a function f(x) with the following properties:
\lim_{x\to-3^-}f(x) = 4,
\lim_{x\to-3^+}f(x) = 2,
\lim_{x\to-1}f(x) = 1,
f(-3) = 3,
and f(x) is continuous everywhere except at x = -3.
Any function that satisfies the properties.
300
Suppose
f(x) = 3x^2 + 7x - 5.
Compute the difference quotient
\frac{f(x+h)-f(x)}{h}.
Make sure that your expression can be evaluated as h approaches 0.
6x+3h+7
300
Suppose that an object is thrown into the air and that its height is measured by
h(t) = -4.9t^2 + 7t+3
in meters at time t seconds. Determine the speed of the speed of the object at time t = 0.
7 meters/second
400
Suppose the position, in meters, of a particle is given by
x(t) = t^3-14t+2
at a given second t. Compute the average speed of the particle from second 3 to second 5.
35 meters/second
400
Suppose that
\lim_{x\to6}f(x) = 3
and
\lim_{x\to6}g(x) = -1.
Compute
\lim_{x\to6}(\frac{x^2+2x+8}{2g(x)^2}-3f(x)).
19
400
Compute
\lim_{x\to\infty}\frac{x^5-7x^2+10x}{x^3-4}.
DNE
400
Find the equation of the tangent line to
f(x) = 4x^2 + 3x - 2
at x = 2.
y = 19x - 18
400
Use the graph of
f(x) = x^{2}-11x+24,
to determine the values of x, if any, for which
|x^{2}-11x+24|
not differentiable.
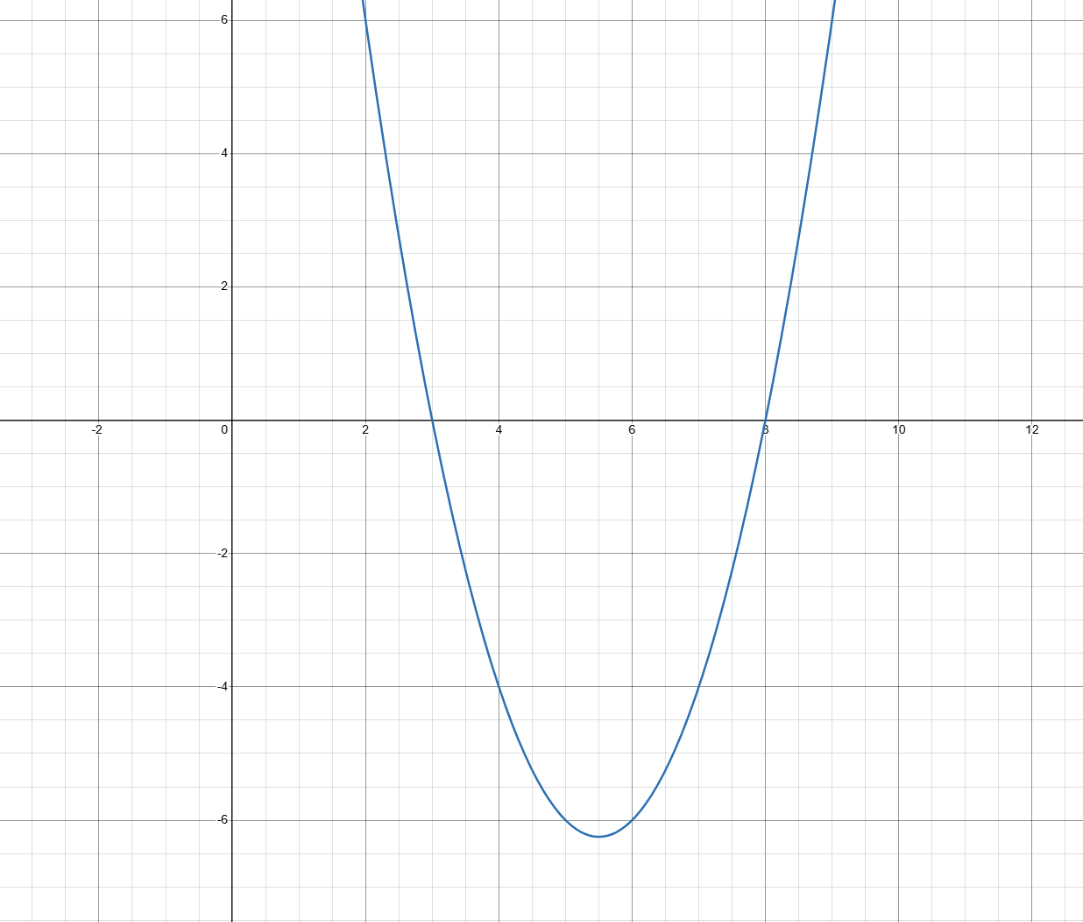
x = 3 and x = 8.
500
Suppose
f(x) = x^2 - 3x + \pi^e
Find a real number A such that the average rate of change from x = 1 to x = A is 2.
A = 4.
500
Compute
\lim_{x\to\infty}\frac{7x + 4x^2+5}{2x^2+10}.
2
500
Compute
\lim_{x\to\infty}\frac{4x^3 + (7 + 13x^2)^4}{-11+4x^9}.
0
500
Suppose
f(x) = x^2 + 4x + 2.
Find a positive value A such that the average rate of change of f(x) from x = 0 to x = A is equal to the slope of the tangent line to f(x) at x = 5.
A = 10.
500
Sketch a function f(x) with the following properties:
\lim_{x\to1^-}f(x) = 2,
\lim_{x\to1^+}f(x) = 5,
\lim_{x\to2^-}f(x) = 1,
\lim_{x\to2^+}f(x) = 3,
and f(x) is continuous everywhere except at x = 1 and x = 2.
Any function that satisfies the properties.