Quadratics
Coordinate Geometry
Circular Measure
Functions
Trigonometry
100
Vertex of
f(x) = 3(x+1)^2 -4
What is (-1, -4)?
100
Rewrite this equation of a circle in standard form:
x^2 - 6x + y^2 + 2y - 6 = 0.
What is its center and radius?
What is (x-3)2+(y+1)2=16, center (3, -1), radius 4?
100
Formula for the area of a sector and length of corresponding arc
A = 1/2r^2\theta ,s=r\theta
100
Let f be a function. Then the domain of f^-1 is ____ and the range of f^-1 is ____.
the range of f, the domain of f
100
What is
sin(240^o), cos(150^o), tan(225^o)?
What is
-\sqrt{3}/2, -1/2, +1?
250
Discriminant of
3x^2 + 10x + 1
What is 88?
250
Equation of the line that passes through the point (3, 4) with gradient 7, in the form y = mx + c.
What is y = 7x - 17?
250
20o in radians
\pi/9
250
Let f(x) = 6x + 7, g(x) = x^2 + 2, x in R. Find the composition
fg(x).
What is
fg(x) = 6x^2 + 19?
250
Sketch
y = tan(4x), 0<=x<=2\pi.
Its period is this.
What is
\pi/4?
750
Solve the equation x4-7x2+12=0.
What is
x = +- \sqrt{3}, +- 2?
750
A circle passes through the points
P(3, \sqrt{10}), Q(0,1), R(3 +\sqrt{6}, 2).
Find the equation of the circle.
What is
(x-3)^2+y^2=10?
750
The diagram shows an equilateral triangle, PQR, with side length 5cm. M is the midpoint of the line QR. An arc of a circle, center P, touches QR at M and meets PQ at X and PR at Y. Find in terms of pi and sqrt(3): the total perimeter of the shaded region and the total area of the shaded region.
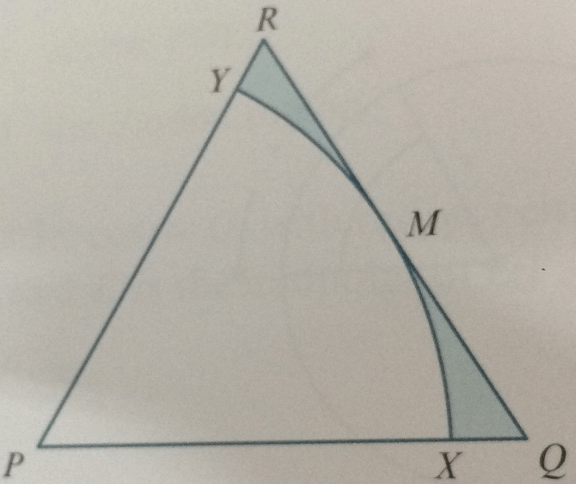
What is
15-5\sqrt{3}+5\sqrt{3}\pi/6, 25\sqrt{3}/4-25\pi/8?
750
Let y = f(x) be the graph of some function. The graph of f is reflected over the x-axis, followed by a translation 3 units upwards, followed by a translation 1 unit to the right, followed by a horizontal stretch with stretch factor 2. The resulting graph is given by
y = -1/2x^2 + 6.
If f(x) = ax2+bx+c, find a, b, and c.
What is a = 2, b = 4, c = -1?
750
Solve the equation
3cos^4\theta +4sin^2\theta-3 = 0, 0^o<=\theta<=180^o .
What is
0^o, 180^o, 54.7^o, 125.3^o?
1500
A curve has equation y = 3x2-8x+7 and a line has equation y = mx, where m is a constant. For the case where m = 2, the curve and the line intersect at the points A and B. Find the coordinates of the mid-point of AB.
What is M = (5/3, 10/3)?
1500
ABCD is a trapezium with AB parallel to DC and angle BAD = 90o. Calculate the coordinates of D, and calculate the area of the trapezium ABCD.
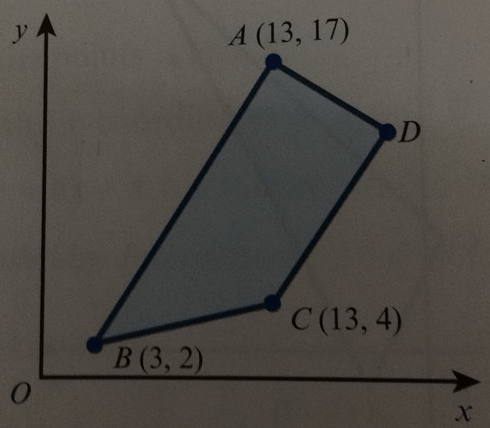
What is (19, 13) and 104?
1500
The diagram shows a circle C1 touching a circle C2 at a point X. Circle C1 has center A and radius 6cm, and circle C2 has center B and radius 10cm. Points D and E lies on C1 and C2 respectively and DE is parallel to AB. Angle DAX = pi/3 radians and angle EBX = theta radians. By considering the perpendicular distances of D and E from AB, find the exact value of theta. Find the perimeter of the shaded region, correct to 4 significant figures.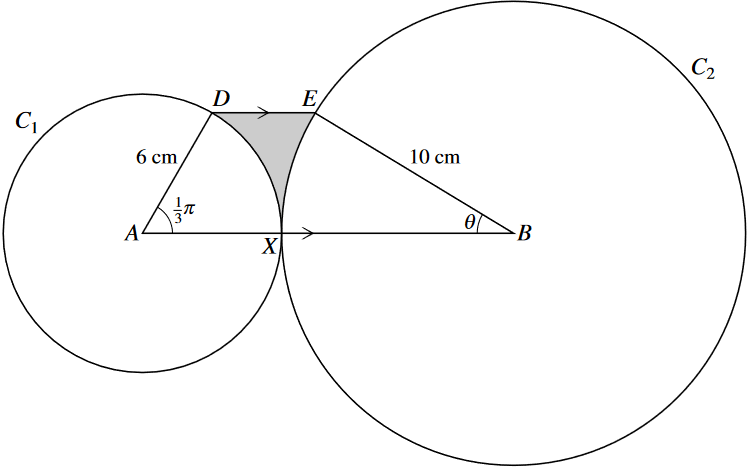
What is
\theta = sin^-1(3\sqrt{3}/10), P = 16.20?
1500
Let f(x)=x2+2x+1 for x <= -1. Find
f^-1(x).
What is
f^-1(x) = -1 - \sqrt{x}?
1500
Sketch, on a single diagram, the graphs of y = cos(3x) and y = 1/10 for 0 <= x <= 2pi. Write down the number of roots of the equation cos(3x) - 1/10 = 0 in the interval 0 <= x <= 2pi. Deduce the number of roots of the equation cos(3x) - 1/10 = 0 in the interval 10pi <= x <= 20pi.
What is 30?
2000
Let f(x) = x2+1 for
x in R
and g(x) = x + 2 for x >= -1. Solve
fg(x) <= 17.
What is
-1 <= x<=2?
2000
The diagram shows a quadrilateral ABCD in which the point A is (-1, -1), the point B is (3, 6) and the point C is (9, 4). The diagonals AC and BD intersect at M. Angle BMA = 90o and BM = MD. Calculate the coordinates of M and D, and the ratio AM:MC.
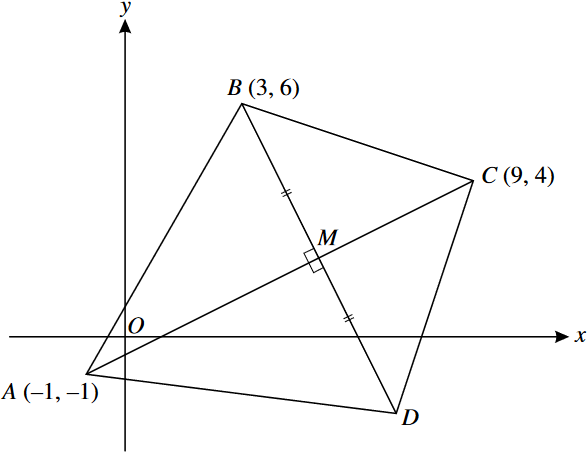
What is D = (7, -2) and 3:2?
2000
The diagram shows a sector of a circle with center O and radius 20cm. A circle with center C and radius x cm lies within the sector and touches it at P, Q, and R. Angle POR = 1.2 radians.
(1) Find x correct to 3 decimal places.
(2) Find the total area of the sector lying outside the circle with center C.
(3) Find the perimeter of the region OPSR bounded by the arc PSR and the lines OP and OR.
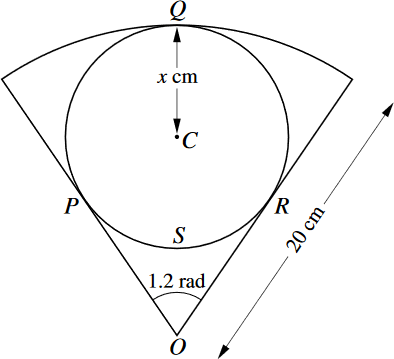
What is
x = 7.218, A = 76.3, P = 35.1?
2000
The function
g:x\mapsto-2x^2+8x-14
is defined for
x>=A.
Find the smallest value of A for which g has an inverse. For this value of A, find an expression for
g^-1(x)
in terms of x.
What is
A=2, g^-1(x) = 2+\sqrt{-1/2x-3}?
2000
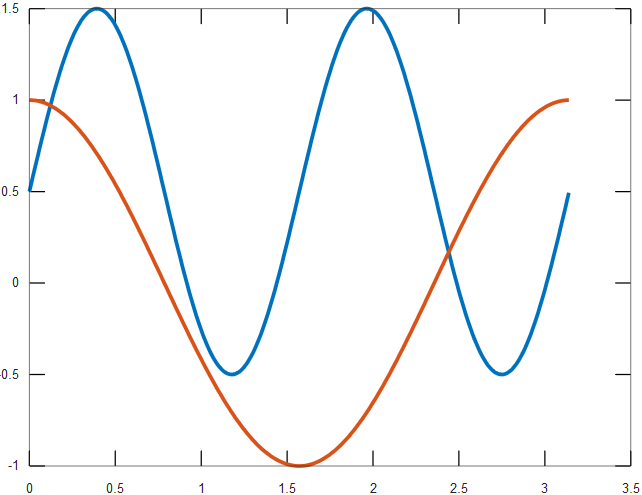
Sketch y = cos(2x) and y = 1/2 + sin(4x) on the same graph. This is the number of solutions does the equation cos(2x) = 1/2 + sin(4x) have on the interval [0, pi].
What is 2?
