Plotting Plotters
Sines of the times
Negative vibes
Count on me
Deriving Accidents
100
Area of the triangle
0.25
100
Sin(A+B)
sin(a) * cos (B) + sin(B) * cos(A)
100
Consider the operation "minus the reciprocal of," defined by a~b = a -1/b. What is ((1~2)~3)-(1~(2~3))?
-7/30
100
Abby the Abacus somehow uses a mower to cut she rectangular 90-foot by 150-foot lawn. The swath she cuts is 28 inches wide, but she overlaps each cut by 4 inches to make sure that no grass is missed. She walks at the rate of 5000 feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Abby to mow the lawn.
1.35
100
An excellent driver crashed 5 times in a math. Each crash either took off 2-3 tires. How many different numbers could represent the total number of tires destroyed?
6
200
4.36
200
Sin(3A)
3sin(a) -4sin^3a
200
Brandon is a herder of anti-cows and cows (each anti-cow counts as a -1 cow). When an anti-cow and a cow meet they disintegrate into steak. Everyday, his herd of anti-cows multiplies by 3 and his herd of cows multiplies by 2. If his farm ends with 10 anti-cows and 10 cows on Day 1, after a week (if the cows and anti-cows all form a pair if possible at the end of the week and disintegrate) how many total cows (each anticow remaining counts as -1 cow) does Brandon have?
-6650 cows or 6650 anticows
200
11111^2+2468
123456789
200
Skier Sophia has an odometer to count the distance she travelled. The odometer records up to 99999m, then flips over to 00000m on the next meter. Sophia plans to determine how far she has travelled for a year. On January 1 Sophia sets the odometer to 00000. During the year, the odometer flips from 99999 to 00000 forty-four times. On December 31 the odometer reads 50000. Sophia takes 1800m per ski trip. Which of the following is closest to the number of ski trips Sophia went on during the year?
2500
300
Area of the polygon
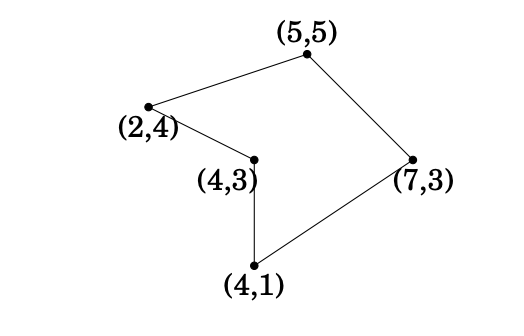
17/2
300
In 100AD, Euthagorstein proved Sin^2(x) + Cos^2(x) =1. Prove it too.
+200 Points for guessing the 3 mathematicians/physicists I used to create the horrendous name.
Go check Brandon
300
Brandon is in debt. Heavy debt.
After running his old fertilizer business into the ground, he's got no money left to spend. Currently, he owes 100000 dollars. His bank offers him a chance to pay next year with interest only if he solves a math problem. If 4^a = 5, 5^b =6, 6^c = 7, and 7^d = 8. a*b*c*d in % is the amount of interest he has to pay. How much will Brandon owe next year?
150000$
300
In the sequence 2001,2002,2003,..., each term after the third is found by subtracting the previous term from the sum of the two terms that precede that term. For example, the fourth term is 2001+2002-2003=2000. What is the 2004th term in this sequence?
0
300
The Titanic sails 10 miles in a straight line from A to B, turns through an angle between 45deg and 60deg, and then sails another 20 miles before crashing into an iceberg. Let AC be measured in miles. The team who gets the closest number to AC^2 gets the points.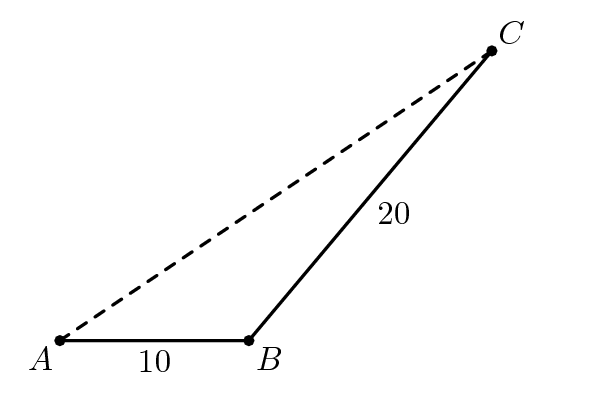
approx 782
400
10/91
400
In triangle ABC, 3sinA + 4cosB = 6 and 4sinB + 3cosA =1. What does <C equal?
30
400
Let a, b, and c be real numbers such that a-7b+8c=4 and 8a+4b-c=7. Then b^2-a^2-c^2 is
-1
400
Let S be the set of permutations of the sequence 1,2,3,4,5 for which the first term is not 1. A permutation is chosen randomly from S. The probability that the second term is 2, in lowest terms, is a/b. What is a+b?
19
400
Brandon and his evil twin Brendan run on a circular track. Brandon runs counterclockwise and completes a lap every 90 seconds, and Brendan runs clockwise and completes a lap every 80 seconds. Both start from the start line at the same time. At some random time between 10 minutes and 11 minutes after they begin to run, a photographer standing inside the track takes a picture that shows one-fourth of the track, centered on the starting line. What is the probability that both Brandon and Brendan are in the picture?
3/16
500
Brandon is plotting to destroy the world one step at a time. But first, he's got to practice manipulating his evil biochemical ant Anand. Anand starts at the origin p0 (0,0) facing to the east and walks one unit, arriving at p1 (0,0). For n = 1,2,3..., right after arriving at the point pn, if Anand can turn 90 degrees left and walk one unit to an unvisited point pn+1, he does that. Otherwise, he walks one unit straight ahead to reach pn+1. Thus the sequence of points continues p2 = (1,1),p3 = (0,1),p4 = (-1,1), p5 =(-1,0), and so on in a counterclockwise spiral pattern. What is p2015?
(13,-22)
500
In the year 3000, Julia, a celebrated scholar, is naturally perturbed with irrationally emanating thaumatological phenomena. The movement of these phenomena can be tracked utilized the equation y = sin(1/x). Guess how many x-intercepts on the graph of sin(1/x) there are in the interval(0.0001,0.001). Closest team gets the point
Closest too 2865
500
Part of the graph of f(x) = ax^3 + bx^2 + cx = d is shown. What is b?
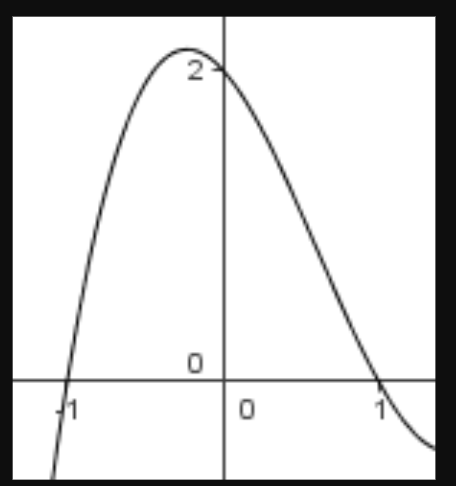
-2
500
Carl the calculator owns a parking lot has 16 spaces in a row. Twelve cars arrive, each of which requires one parking space, and their drivers chose spaces at random from among the available spaces. Hans the human then arrives in his SUV, which requires 2 adjacent spaces. The the probability that he is able to park is a/b. What is A+B?
45.
500
A regular octahedron has side length 1. A plane parallel to two of its opposite faces cuts the octahedron into the two congruent solids. The polygon formed by the intersection of the plane and the octahedron has area a*sqrt(b)/c, where a, b, and c are positive integers, a and c are relatively prime, and b is not divisible by the square of any prime. What is a+b+c?
14