Question 6b
A family company makes birthday cakes, all of which are sold to its customers. There is a fixed cost of $3,000 each week and an additional production cost of $15 per cake. Each cake sells for $40.
Let x = the number of cakes made each week.
Write down the weekly revenue function.
R(x)=40x " in dollars"
Question 16a
Consider a polynomial of the form
p(x)=ax(x^6-1), "where " a!=0 " is a constant".
What is the degree of p(x)?
p(x)=ax^7-ax
"degree"=7
Question 8b
Consider the trigonometric function
f(x)=4+3cos(pi/2(x-1))
"What is the period of " f(x)
Period = (2pi)/(pi/2)=4
Question 20a
A biologist is interested in the growth of a certain kind of algae in a large tank in response to a particular nutrient. It is found that the mass (kg) of algae in the tank after t hours from when the nutrient is added is given by
f(t)=2+(8(e^t-1))/(e^t+20)
Find the exact mass of the algae in the tank when the nutrient is added.
"mass "=f(0)=2+(8(1-1))/(1+20)=2kg
"Question 3c"
"Line 1: " y=1/3x+4
"Line 2: " y=-2x+15
Are the lines perpendicular, parallel, or neither? Give reasons.
Lines are not perpendicular since m1*m2=1/3(-2)!=-1
Lines are not parallel since m1=1/3!=m2=-2
Question 7b
Consider the following matrices.
A=[[3,x],[-2,4]] " " B=[[-1,2],[3,0],[0,4]] " " C=[[2,0,5],[-2,0,3]]
"Where possible evaluate the following, showing all working."
"If not possible, give the reason."
"Evaluate: " AB
Not possible since number of columns of A (2) is not equal to the number of rows of B (3)
Question 10
Evaluate, showing all working.
||1+2|-|3-8||
=|3-|-5||
=|3-5|
=|-2|
=2
Question 16b
Consider a polynomial of the form
p(x)=ax(x^6-1), "where " a!=0 " is a constant".
For each of the following statements, decide if it is true or false.
"i) If " a>0 ", then " p(x)->oo " as " x->oo
"ii) If " a<0 ", then " p(x)->oo " as " x->-oo
i) True
ii) True
Question 8c
Consider the trigonometric function
f(x)=4+3cos(pi/2(x-1))
"What are the maximum and minimum values for" f(x)
"Maximum value " = 4+3xx1=7
"Minimum value "=4+3(-1)=1
Question 20b
A biologist is interested in the growth of a certain kind of algae in a large tank in response to a particular nutrient. It is found that the mass (kg) of algae in the tank after t hours from when the nutrient is added is given by
f(t)=2+(8(e^t-1))/(e^t+20)
"Find the exact mass of algae in the tank at time " t=ln(12) " hours"
"mass " =f(ln12)=2+(8(12-1))/(12+20)
=2+11/4
=19/4kg
Question 6c
A family company makes birthday cakes, all of which are sold to its customers. There is a fixed cost of $3,000 each week and an additional production cost of $15 per cake. Each cake sells for $40. Given the following cost and revenue functions, how many cakes must be made and sold each week for the company to break even?
C(x)=3000+15x " ($)"
R(x)=40x " ($)"
"Break even when " R(x)=C(x)
40x=3000+15x
25x=3000
x=120
Need to make 120 cakes each week to break even.
Question 7c
Consider the following matrices.
A=[[3,x],[-2,4]] " " B=[[-1,2],[3,0],[0,4]] " " C=[[2,0,5],[-2,0,3]]
"Where possible evaluate the following, showing all working."
"If not possible, give the reason."
"Evaluate: " BA
=[[-1,2],[3,0],[0,4]][[3,x],[-2,4]]
=[[-3-4,-x+8],[9,3x],[-8,16]]
=[[-7,-x+8],[9,3x],[-8,16]]
Question 9
Simplify the following expression
((x+y)^4(y^2x)^3z^4)/((36x^8)^(1/2)y^5(x+y)^-1)
=((x+y)^5y^6z^3z^4)/(6x^4y^5)
((x+y)^5yz^7)/(6x^4)
Question 18c
Evaluate the following limits where they exist, showing all working.
lim_(x->0)(5x^3+x^2-4x)/(x^2+2x)
=lim_(x->0)(x(5x^2+x-4))/(x(x+2))
=lim_(x->0)(5x^2+x-4)/(x+2)
=(0+0-4)/(0+2)
=-2
Question 12a
Differentiate the following functions, showing all working and simplifying your answer.
f(x)=8-5sqrt(x)+4x^-5
f(x)=8-5x^(1/2)+4x^-5
f'(x)-5/2x^(-1/2)-20x^-6
Question 1
Evaluate the following expression. Make sure you show all working and give the exact answer.
24"/"6(-2)+[sqrt(25)+(7-5)^2]"/"3+12"/"4-2
=4(-2)+(5+4)"/"3+3-2
=-8+3+3-2
=-4
Question 7d
Consider the following matrices.
A=[[3,x],[-2,4]] " " B=[[-1,2],[3,0],[0,4]] " " C=[[2,0,5],[-2,0,3]]
"Where possible evaluate the following, showing all working."
"If not possible, give the reason."
"Evaluate: " CB-2A
=[[2,0,5],[-2,0,3]][[-1,2],[3,0],[0,4]]-2[[3,x],[-2,4]]
=[[-2,24],[2,8]]-[[6,2x],[-4,8]]
=[[-8,24-2x],[6,0]]
Question 19b
Consider the following rational function.
f(x)=(x^2+2x-8)/(6x-2x^2)
Find all the vertical asymptotes of f(x) (if they exist), showing all working.
"denominator of " f(x)=x(6-2x)=0
"when " x=0, x=3
"as " x->0," numerator" ->-8 !=0
"as " x->3," numerator" ->7 !=0
:. "Vertical asymptotes are " x=0, x=3
Question 4a
Find the following, simplifying your answer. Use calculus and show all your working.
int " "2t^(2/3)-4t+3t^-3 dt
=(2t^(5/3))/(5/3)-(4t^2)/2+(3t^-2)/-2+C
=6/5t^(5/3)-2t^2-3/2t^-2+C
Question 12b
Differentiate the following functions, showing all working and simplifying your answer.
g(x)=(2t+3)/(t^2-4)
g'(t)=((t^2-4)2-(2t+3)2t)/((t^2-4)^2)
=(2t^2-8-4t^2-6t)/((t^2-4)^2)
=(-2t^2-6t-8)/((t^2-4)^2)
Question 20c
A biologist is interested in the growth of a certain kind of algae in a large tank in response to a particular nutrient. It is found that the mass (kg) of algae in the tank after t hours from when the nutrient is added is given by
f(t)=2+(8(e^t-1))/(e^t+20)
"Find the exact time at which the mass of algae in the tank equals 4kg."
f(t)=2+(8(e^t-1))/(e^t+20)=4
8(e^t-1)=2(e^t+20)
4e^t-4=e^t+20
3e^t=24
e^t=8
:. "time is " t=ln(8) " hours"
Question 3a
Line 1 is defined by slope m=1/3 and y-intercept c=4. Line 2 passes through the points (6,3) and (4,7).
Find the equation of these two lines.
"Line 1: " y=1/3x+4
"Line 2: slope " m=(7-3)/(4-6)=4/-2=-2
y=-2x+c
"Substitute " x=6, y=3 " get: "
3=-12+c
c=15
:.y=-2x+15
Question 13
Rewrite the following expression with a common denominator and simplify your answer.
(3x+4)/(x+2)-(x+3)/(2x-3)
=((3x+4)(2x-3)-(x+3)(x+2))/((x+2)(2x-3)
=(6x^2-x-12-(x^2+5x+6))/((x+2)(2x-3))
=(5x^2-6x-18)/((x+2)(2x-3))
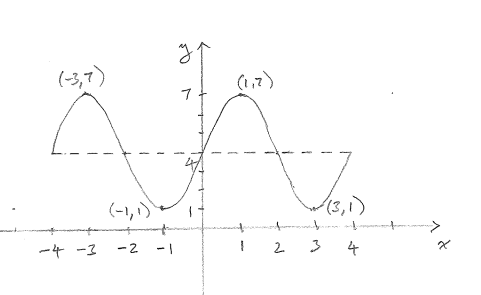
Question 8b
Consider the trigonometric function. Sketch the graph of the function
f(x) " for " x in[-4,4]
"clearly labelling the locations of the maxima and minima of the function."
f(x)=4+3cos(pi/2(x-1))
"Amplitude"=3
"Period"=4
"Minimum value"=1
"Maximum value"=7
Question 4b
Find the following, simplifying your answer. Use calculus and show all your working.
int_1^4 " " x^(1/2)+4x^-2-3 dx
=2/3x^(3/2)+(4x^-1)/-1-3x |_1^4
=2/3xx4^(3/2)-4xx4^-1-3xx4-(2/3-4-3)
=16/3-1-12-2/3+4+3
=14/3-6
=-4/3
Question 12c
Differentiate the following functions, showing all working and simplifying your answer.
f(x)=(3x^2-4x)e^(2x)
f'(x)=(3x^2-4x)2e^(2x)+(6x-4)e^(2x)
=(6x^2-8x+6x-4)e^(2x)
(6x^2-2x-4)e^(2x)
Question 20d
A biologist is interested in the growth of a certain kind of algae in a large tank in response to a particular nutrient. It is found that the mass (kg) of algae in the tank after t hours from when the nutrient is added is given by
f(t)=2+(8(e^t-1))/(e^t+20)
Find (in simplified form) the rate of increase of the algae mass at any time t>0
rate of increase is
f'(t)=0+((e^t+20)8e^t-8(e^t-1)e^t)/((e^t+20)^2)
=(8e^(2t)+160e^t-8e^(2t)+8e^t)/((e^t+20)^2)
=(168e^t)/((e^t+20)^2) "kg/hr"