Formulas
Intersections
Objectives
Translate
Checking Answers
100
Solve for h if SA=94, l=5, and w=4.
SA=2lh+2wh+2lw
h=3
100
Find the corner point A.
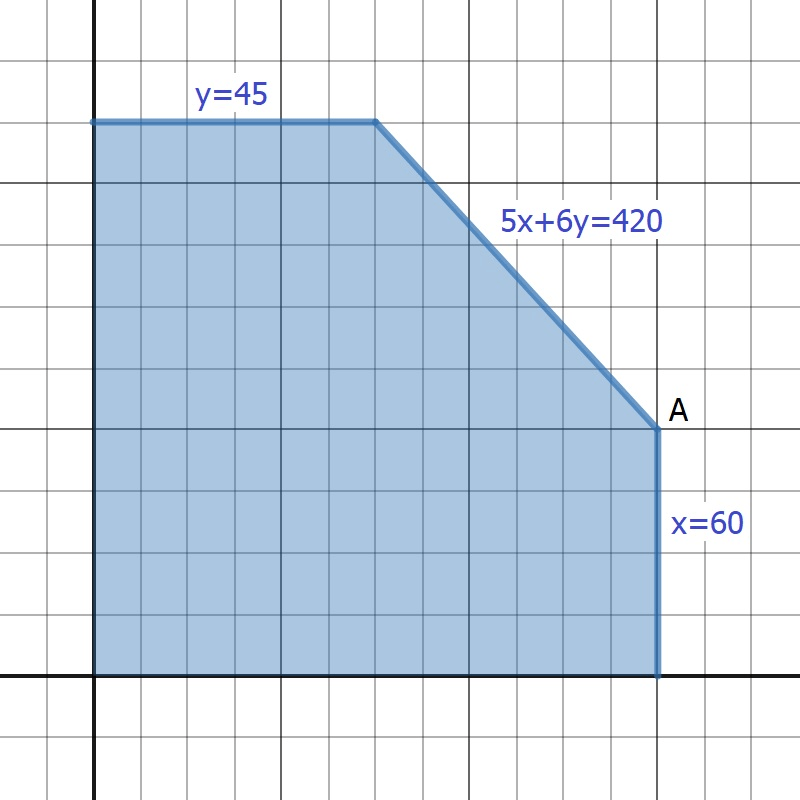
A \rightarrow (60,20)
100
If the objective function is
z=3x+2y
and the corner points are
(0,0) \quad (0,2) \quad (2,1) \quad (1,0)
find the maximum value.
The maximum value is 8 at corner (2,1).
100
Write a system of equations for the following problem.
A manufacturer of tennis rackets makes a profit of $15 on each oversized racket and $8 on each standard racket. To meet dealer demand, daily production of standard rackets should be between 30 and 80, and production of oversized rackets should be between 10 and 30. To maintain high quality, the total number of rackets produced should not exceed 80 per day. How many of each type should be manufactured daily to maximize profit?
Let x represent the number of oversized rackets produced and let y represent the number of standard rackets produced.
{(10,\leq,x,\leq,30),(30,\leq,y,\leq,80),(x,+,y,\leq,80):}
100
Determine which of the following points are part of the graph of the system of linear inequalities.
{(2x,-,y,\leq,4),(x,+,y,\geq,-1):}
The points for consideration are
(6,0) \quad (3,5) \quad (0,0) \quad (3,-2)
The points (1,1) and (2,3) are part of the graph.
200
Solve for a if S=105/128 and r=-1/2.
S=\frac{a(1-r^6)}{1-r}
a=\frac{5}{4}
200
Find the corner point A.
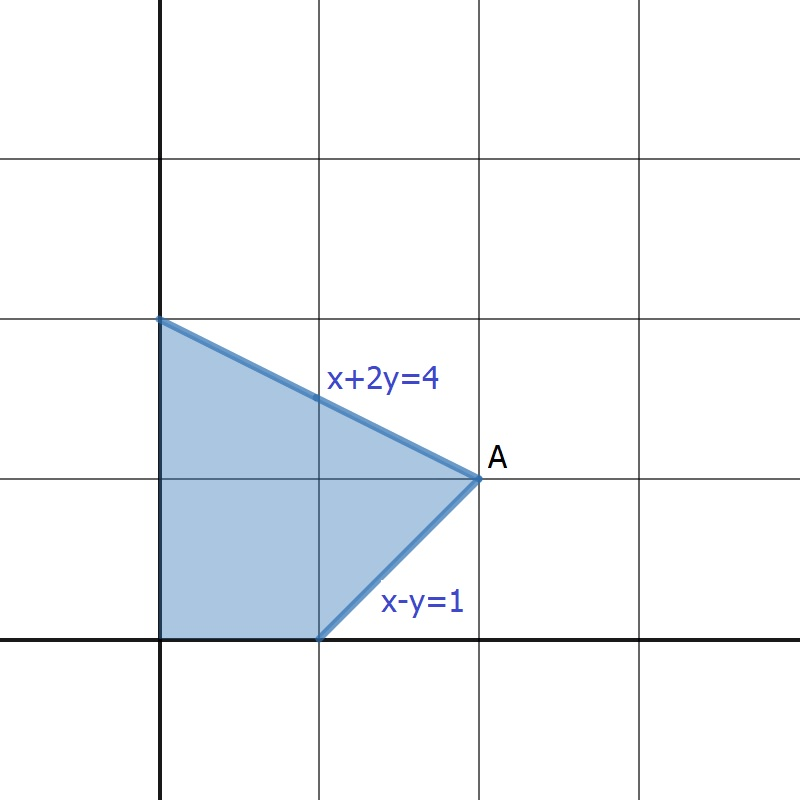
A \rightarrow (2,1)
200
Given the objective function
z=4x+2y
and the corner points
(1,4) \quad (2,1) \quad (4,0)
what is the minimum value?
The minimum value is 10 at corner point (2,1).
200
Write a system of equations for the following problem.
A company produces two types of tables, dining tables and coffee tables. It takes 2 hours to produce the parts of one dining table, 1 hour to assemble and 2 hours to polish. It takes 4 hours to produce the parts of one coffee table, 2.5 hour to assemble and 1.5 hours to polish. Per month, 7000 hours are available for producing the parts, 4000 hours for assembling the parts and 5500 hours for polishing the tables. The profit per dining table is $90 and per coffee table is $110. How many of each type of tables should be produced in order to maximize the total monthly profit?
Let x represent the dining tables produced and let y represent the coffee tables produced.
{(2x,+,4y,\leq,7000),(x,+,2.5y,\leq,4000),(2x,+,1.5y,\leq,5500):}
200
Determine which of the following points are part of the graph of the system of linear inequalities.
{(2x,+,y,\leq,6),(x,-,y,\geq,3):}
The points for consideration are
(6,0) \quad (3,5) \quad (0,0) \quad (3,-2)
The point (3,-2) is part of the graph.
300
Solve for c if x=-3, a=1, and b=5/2.
x=\frac{-b\-\sqrt{b^2-4ac}}{2a}
c=\frac{-3}{2}
300
Find the corner points A and B.
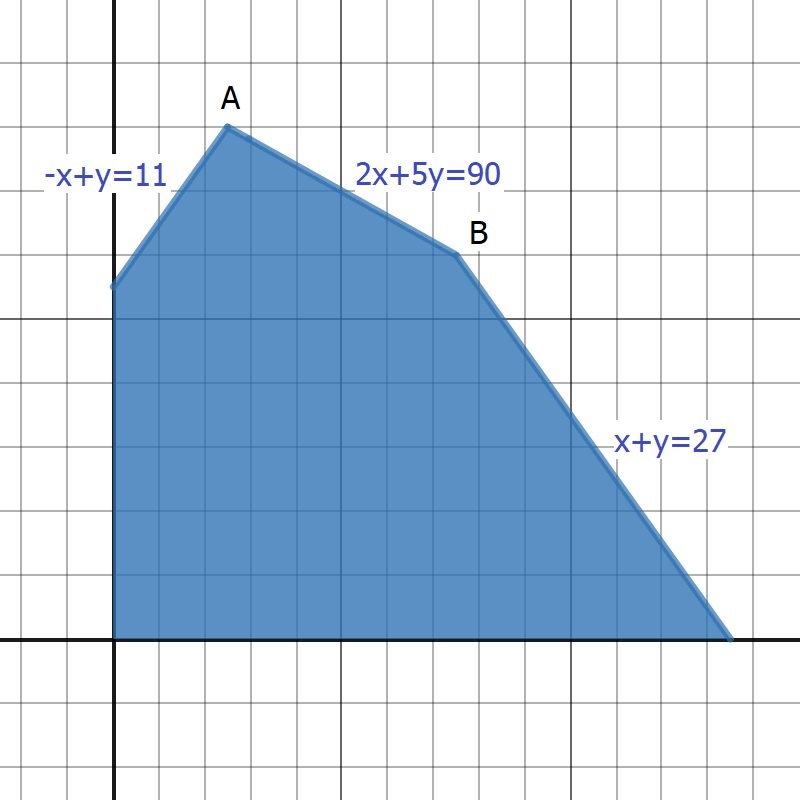
A \rightarrow (5,16), B \rightarrow (15,12)
300
The objective function is
z=4x+2y
The graph of the constraints is
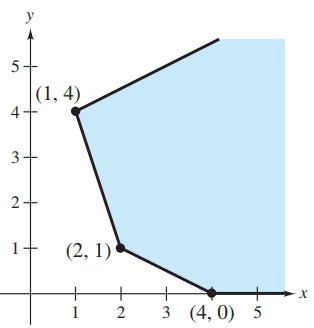
There is no maximum value. The region is unbounded.
300
Write a system of equations for the following problem. Also write an objective function.
Bob builds tool sheds. He uses 10 sheets of dry wall and 15 studs for a small shed and 15 sheets of dry wall and 45 studs for a large shed. He has available 60 sheets of dry wall and 135 studs. If Bob makes $390 profit on a small shed and $520 on a large shed, how many of each type of building should Bob build to maximize his profit?
Let x represent the number of small sheds and let y represent the number of large sheds.
{(10x,+,15y,\leq,60),(15x,+,45y,\leq,135):}
z=390x+520y
300
Determine which of the following points are part of the graph of the system of linear inequalities.
{(x,+,y,\geq,2),(2x,+,y,\geq,3),( , ,x,\geq, 0),( , , y,\geq,0):}
The points for consideration are
(6,0) \quad (3,5) \quad (0,0) \quad (3,-2)
The points (3,2) and (1,1) are part of the graph.
400
Solve for R if S=201,452.10, i=0.06.
S=R[\frac{(1+i)^n-1}{i}]
R=24,000
400
Find corner points A and B.
A \rightarrow (\frac{55}{14},\frac{24}{7}), B \rightarrow (\frac{25}{2},0)
400
The objective function is
z=4x+6y
The corner points are
(0,0) \quad (0,11) \quad (5,16) \quad (15,12) \quad (27,0)
What is maximum value?
The maximum value is 132 at corner point (15,12).
400
Write a system of equations for the following problem. Also write an objective function.
A manufacturer of ski clothing makes ski pants and ski jackets. The profit on a pair of ski pants is $2.00 and on a jacket is $1.50. Both pants and jackets require the work of sewing operators and cutters. There are 60 minutes of sewing operator time and 48 minutes of cutter time available. It takes 8 minutes to sew one pair of ski pants and 4 minutes to sew one jacket. Cutters take 4 minutes on pants and 8 minutes on a jacket.
Let x represent the ski pants produced and let y represent the ski jackets produced.
{(8x,+,4y,\leq,60),(4x,+,8y,\leq,48):}
z=2x+1.50y
400
Determine which of the following points are part of the graph of the system of linear inequalities.
{(2x,-,y,\leq,-4),(2x,-,y,\leq,-2),(x,+,2y,\geq,6):}
The points for consideration are
(1,1) \quad (1,5) \quad (3,11) \quad (-1,1)
The point (3,11) is part of the graph.
500
Solve for P if R=1319.01, i=0.005, and n=360.
R=\frac{P i}{1-(1+i)^{-n}}
P=220,000
500
Find corner points A, B and C.
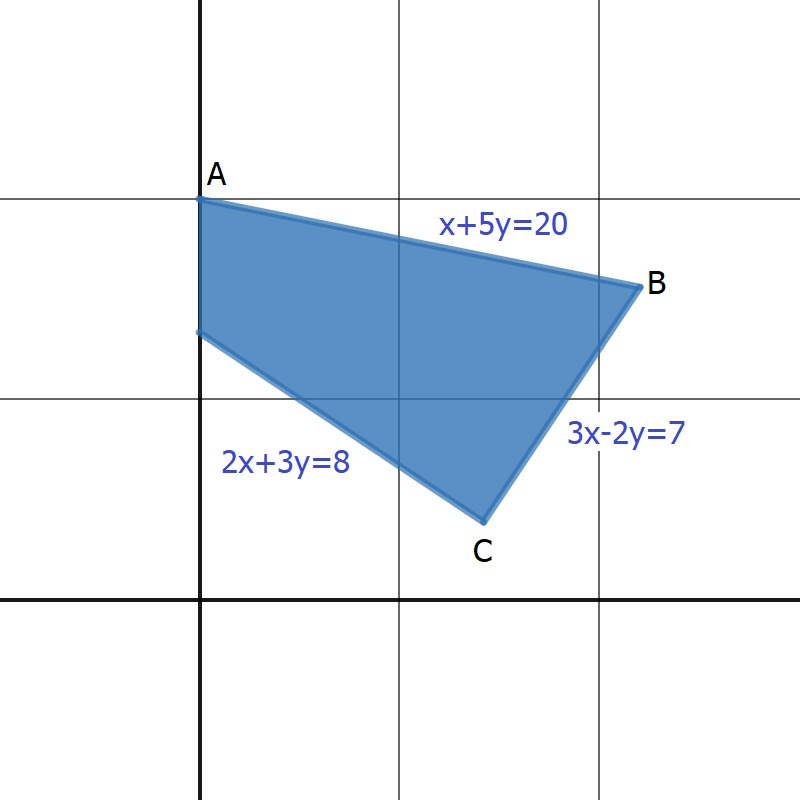
A \rightarrow (0,4), B \rightarrow (\frac{75}{17},\frac{53}{17}), C \rightarrow (\frac{37}{13},frac{10}{13})
500
The objective function is
z=5x+7y
The corner points are
(0,2) \quad (0,4) \quad (1,5) \quad (6,3) \quad (5,0) \quad (3,0)
Find the minimum value.
The minimum value is 14 at (0,2).
500
Write a system of equations for the following problem. Also write an objective function.
In order to ensure optimal health (and thus accurate test results), a lab technician needs to feed the rabbits a daily diet containing a minimum of 24 grams (g) of fat, 36 g of carbohydrates, and 4 g of protein. But the rabbits should be fed no more than five ounces of food a day. Rather than order rabbit food that is custom blended, it is cheaper to order Food X and Food Y, and blend them for an optimal mix. Food X contains 8 g of fat, 12 g of carbohydrates, and 2 g of protein per ounce, and costs $0.20 per ounce. Food Y contains 12 g of fat, 12 g of carbohydrates, and 1 g of protein per ounce, at a cost of $0.30 per ounce. What is the optimal blend of Food X and Food Y?
Let x represent the amount of Food X and let y represent the amount of Food Y.
{(8x,+,12y,\geq,24),(12x,+,12y,\geq,36),(2x,+,y,\geq,4),(x,+,y,\leq,5):}
0.20x+0.30y=z
500
Determine which of the following points are part of the graph of the system of linear inequalities.
{(2x,+,3y,\leq,9),(3x,+,2y,\geq,4),(x,-,2y,\leq,0),( , ,x,\geq,0),( , ,y,\geq,0):}
The points for consideration are
(1,2) \quad (2,1) \quad (4,3) \quad (0,3)
The points (1,2), (2,1), and (0,3) are part of the graph.