Domains and Ranges
Graphs of Functions
Transformations
Combo & Compo
Inverse Functions
Quadratic Functions
100
This is the domain for the parent function
f(x)=1/x
What is
(-\infty,0)\cup(0,\infty)?
100
This is a behavior we observe when functions have negative slope on an interval, i.e., as you move from left to right, the value of the function keeps falling.
What is decreasing?
100
This type of transformation shifts the graph left to right or up to down.
What is a rigid transformation OR (vertical/horizontal) translation?
100
What are the five operations that appear in combination of functions?
What is addition, subtraction, multiplication, division, and composition?
100
A function has this if the function is one-to-one.
What is an inverse?
100
This is a technique that is used to derive the vertex form of a quadratic function.
What is completing the square?
200
The domain and range of the graphed function:
What is
(-\infty,2)\cup(2,4)\text{ and }[-2,\infty)?
200
This type of function holds a property of having rotational symmetry around the origin.
What is an odd function?
200
This type of transformation occurs when the scaling constant of the function is negative.
What is a reflection?
200
Consider the following table:
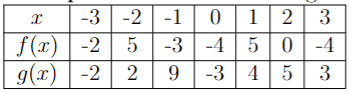This is the evaluation of
(g/f)(-1)
What is -3?
200
This is the result we get when we compose a function it its own inverse.
What is
(f\circ\f^-1)(x)=x?
200
This is the vertex form written algebraically.
What is
f(x)=a(x-h)^2+k?
300
The domain of the quadratic function:
f(x)=-2(x-1)^2+5
What is
(-\infty,5)?
300
This function is either odd, even, or neither.
f(x)=root(3)(2-x^2
What is even?
300
This is the general formula of the transformation form of a function.
What is
y=Af(B(x-h))+k?
300
Consider the functions
f(t)=t^2+3, g(t)=\sqrt(t-2)
This is the composition
(f\circg)(t).
What is
t+1?
300
The inverse of the function:
h(x)=(4x-1)/(2x)
What is
h^-1(x)=-1/(2x-4)?
300
This is the x-intercepts of the following quadratic function:
f(x)=3(x-3)^2-4
What is
(3+\sqrt(4/3),0),(3-\sqrt(4/3),0)?
400
The domain of the following function:
g(x)=(\sqrt(4x-2))/(x^2-16)
What is
[1/2,4)\cup(4,\infty)?
400
This is the function that is even, possesses the domain of
(-\infty,0)\cup(0,\infty)
and behaves as the graph:
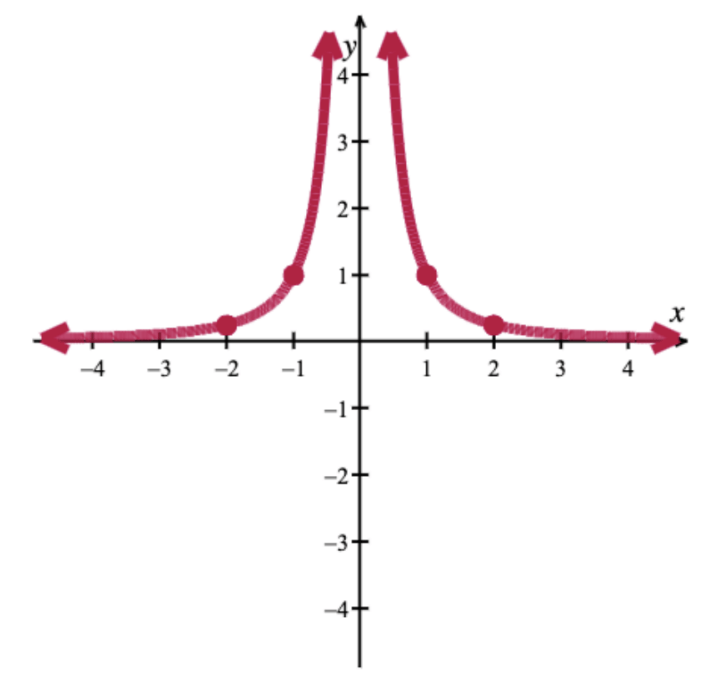
What is
f(x)=1/x^2
or the squared reciprocal function?
400
The formula of the transformed function:
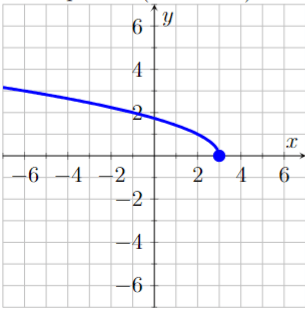
What is
f(x)=\sqrt(3-x)?
400
(DAILY DOUBLE) This is the process in finding the domain of the function resulting in division:
f(x)/g(x)
What is determining the domain of f and g and excluding points where x = 0?
400
The inverse for the function:
f(x)=-root(3)(x+1)+2
What is
f^-1(x)=(2-x)^3+1?
400
These are the roots/zeroes of the following function:
f(x)=(4x-1)^2-2(4x-1)+1
What is
x=1/2?
500
The range of the inverse function for a given domain of the function:
[-3,2)\cup(2,\infty)
What is
[-3,2)\cup(2,\infty)?
500
(DAILY DOUBLE) This is the piecewise function of the following graph:
What is
f(x)={((x-4)^2, x<-2),(abs{x}-3,-2<=x<=2),(\sqrt{8-x},x>2):}
500
Why isn't there typically a horizontal scaling component B (in the transformation form) in a quadratic function?
Because it can be rewritten as a horizontal scaling component itself:
f(x)=x^2
f(2x)=(2x)^2
f(2x)=4x^2
where A = 4.
500
Consider the functions
f(x)=2+1/x, g(x)=x^2+5x
This is the domain of the composite function
(f\circg)(x)
What is
(-\infty,-5)\cup(-5,0)\cup(0,\infty)?
500
This graphical behavior is only observed when all the points from the inverse maps on the original function.
What is "the function is its own inverse", i.e.
f(x)=f^-1(x)?
500
A rancher has 240 feet of fence with which to enclose three sides of a rectangular pasture (the fourth side is a river and will not require fencing). The answer is the dimensions of the pasture with the largest possible area.
What is 120ft x 60ft?