Indicate whether the following are probability distributions (YES/NO). If the distribution does represent a probability distribution find the mean and standard deviation.
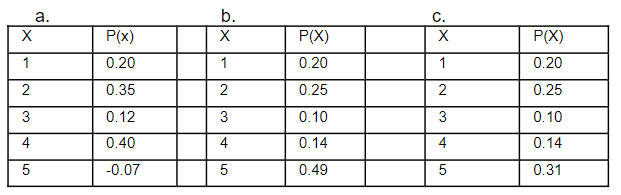
a) Not a probability distribution
b) Not a probability distribution
c) Probability distribution
mu=3.11, sigma=1.55
Find the critical value
z_(alpha//2)
that corresponds to an 86% confidence interval.
z_(alpha//2)=1.476
In a poll of 600 randomly selected subjects, 240 answered “yes” when asked if they planned to vote in a state election. Construct a 95% confidence interval
estimate of the proportion of all who plan to vote in that election.
1-PropZInt
n = 600 x = 240 95% CL
Answer: (0.3608,0.4392)
Blood platelet counts of women have a bell-shaped distribution with a mean of 280 and a standard deviation of 65. Using the empirical rule, find the following:
a) About ________% of all values fall within 1 standard deviation of the mean
(between ________ and _______)
b) About ________% of all values fall within 2 standard deviations of the mean
(between ________ and _______)
c) About ________% of all values fall within 3 standard deviations of the mean
(between ________ and _______)
a) About 68% of all values fall within 1 standard deviation of the mean (between 215 and 345)
b) About 95% of all values fall within 2 standard deviations of the mean (between 150 and 410)
c) About 99.7% of all values fall within 3 standard deviations of the mean (between 85 and 475)
A Wendy’s manager performed a study to determine a probability distribution for the number of people, X, standing in line during lunch. The results were as
follows:
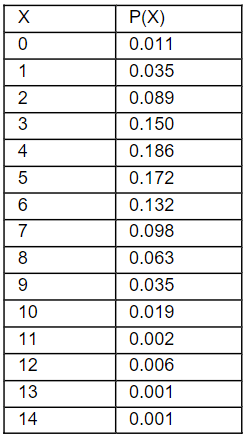
a) Find the expected number of people waiting in line after lunch?
b) Is it usual to have 9 people standing in line?
c) Find the probability that at least 1 person is standing in line.
d) Find the variance.
a) 4.875 people
b) No
c) 0.989
d) 5.04
The math SAT scores for women are normally distributed with a mean of 496 and a standard deviation of 108.
If a woman who takes the math portion of the SAT is randomly selected, find the probability that her score is above 500.
P(x > 500) = normalcdf(500,9999,496,108) = 0.4852
The tobacco industry closely monitors all surveys that involve smoking. One survey showed that among 785 randomly selected subjects who completed four years of college, 18.3% smoke. Hint: You will need to find x, because you know
hat(p)
a. Construct the 95% confidence interval for the true percentage of smokers among all people who completed four years of college.
b. Based on the result form part a, does the smoking rate for those with four
years of college appear to be substantially different than the 27% rate for the
general population?
1-PropZInt
x=hat(p)*n=144
n = 785 95% CL
a) (0.1565,0.2105)
b) Yes, 27% is higher than the range in the 95% confidence interval. It appears that those with 4 years of college smoke at a lower rate than the general population.
A theater group holds a fund-raiser. It sells 100 raffle tickets for $5 apiece. Suppose you purchase four tickets. The prize is two passes to a Broadway show, worth a total of $150.
Construct the probability distribution.
If this fund-raiser is repeated often and you always purchase four tickets, what would be your expected average winnings per raffle?
Expected Value = -$14
You expect to lose $14 per raffle on average.
A school newspaper reporter decides to randomly survey 12 students to see if they will attend Tet (Vietnamese New Year) festivities this year. Based on past years, she knows that 18% of students attend Tet festivities. We are interested in the number of students who will attend the festivities.
- Find the probability that exactly 5 students will attend.
- Find the probability that at most four students will attend.
- Find the probability that more than two students will attend.
- How many of the 12 students do we expect to attend the festivities?
a) binompdf(12,0.18,5) = 0.0373
b) binomcdf(12,0.18,4) = 0.9511
c) 1 - binomcdf(12,0.18,2) = 0.3702
d)
mu=n*p=0.18*12=2.2
The math SAT scores for women are normally distributed with a mean of 496 and a standard deviation of 108.
What is the probability that a woman’s score is between 300 and 500?
P(300 < x < 500) = normalcdf(300,500,496,108) = 0.48
Find the sample size required to estimate the percentage of college students who use loan to help fund their tuitions. Assume that we want 95% confidence that the proportion from the sample is within two percentage points of the true population percentage.
n = ((1.96)^2*0.25)/(0.02)^2 = 2401
Determine whether the New York Yankees or the Philadelphia Phillies had a relatively better run producing season. The Yankees scored 968 runs and play in the American League, where the mean number of runs scored was 793.9 and the standard deviation was 73.5 runs. The Phillies scored 892 runs and play in the National League, where the mean number of runs scored was 763.0 and the standard deviation was 58.9 runs.
z-score for Yankees: z = 2.4
z-score for Phillies: z = 2.2
The Yankees had a relatively better run producing season.
At The Fencing Center, 60% of the fencers use the foil as their main weapon. We randomly survey 25 fencers at The Fencing Center. We are interested in the number of fencers who do not use the foil as their main weapon.
- How many are expected to not to use the foil as their main weapon?
- Find the probability that six do not use the foil as their main weapon.
- Based on numerical values, would you be surprised if all 25 did not use foil as their main weapon? Justify your answer numerically.
a)
mu =n*p=25*0.40=10
b) P(x = 6) = binompdf(25,0.40,6) = 0.0442
c) P(x = 25) = binompdf(25,0.40,25) = 0. The probability that all 25 not use the foil method is almost zero. Therefore, it would be very surprising.
The math SAT scores for women are normally distributed with a mean of 496 and a standard deviation of 108.
What is the probability that a woman’s score is less than 400?
P(x < 400) = normalcdf(-9999,400,496,108) = 0.1870
In a survey of randomly selected subjects, the mean age of the 36 respondents is 40 years and the standard deviation of the ages is 10 years. Use
these sample results to construct a 95% confidence interval estimate of the mean age of the population from which the sample was selected.
TInterval
bar(x)=40
s = 10 n = 36 95% CL
Answer: (36.6, 43.4)
A game involves selecting a card from a regular 52-card deck and tossing a coin. The coin is a fair coin and is equally likely to land on heads or tails.
- If the card is a face card, and the coin lands on Heads, you win $6
- If the card is a face card, and the coin lands on Tails, you win $2
- If the card is not a face card, you lose $2, no matter what the coin shows.
- Find the expected value for this game (expected net gain or loss).
- Should you play this game to win money?
a) E = -$0.62
b) You should not play because you expect to lose $0.62 per game, on average.
The math SAT scores for women are normally distributed with a mean of 496 and a standard deviation of 108.
If the scores in the top 2% will be recognized as exceptionally high, what is the cut-off score for women taking the math SAT?
Round to the nearest whole number.
SAT score = invNorm(0.98,496,108) = 718
Find the sample size required to estimate the mean age of registered drivers in the United States. Assume that we want 99% confidence that the sample mean is within 1/2 year of the true mean age of the population. Also assume that the standard deviation of the population is known to be 12 years.
n=[(2.576*12)/0.5]^2=3823
The serum cholesterol levels in men aged 18-24 are normally distributed with a mean of 178.1 and a standard deviation of 40.7.
a) If one man aged 18 - 24 is randomly selected, find the probability that his serum cholesterol level is greater than 260.
b) If 9 men aged 18 -24 are randomly selected, find the probability that their mean serum cholesterol level is above 260.
a) P(x > 260) = normalcdf(260,9999,178.1,40.7) = 0.0221
b) P(M > 260) = normalcdf(260,9999,178.1,40.7/sqrt9) = 7.9 x 10^-10 = 0.00000000079
Data was collected measuring the accuracy of wristwatches. The times (sec) below show the discrepancy between the real time and the time indicated on the wristwatch. Negative values correspond to watches that are running ahead of the actual time. The data satisfy a loose requirement of appearing to come from a normally distributed population. Construct a 95% confidence interval estimate of the mean discrepancy for the population of wristwatches.
-85 325 20 305 -93 15 282 27 555 570 -241 36
TInterval - Data
95% CL
Answer: (-22.1,308.1) seconds