Which Test?
Which Test?
Which Test?
100
A test of abstract reasoning is given to a random sample of students before and after they completed a formal logic course. Use a 0.05 significance level to test the claim that taking a formal logic course improves students scores on the abstract reasoning test.
Before: 74 83 75 88 84 63 93 84 91 77
After: 73 77 70 77 74 67 95 83 84 75
Should students pay extra money to take the logic course?
H_0:mu_d=0, H_1:mu_d>0
T-Test: t = -2.37, p-value = 0.9789
Fail to reject H0
There is not sufficient evidence to support the claim that taking a formal logic course improves students scores on the abstract reasoning test.
No, students should not pay extra money to take the logic course.
100
In a poll of 745 randomly selected adults, 591 said that it is morally wrong to not report all income on tax returns. Use a 0.01 significance level to test the claim that 75% of adults say that it is morally wrong to not report all income on tax returns.
H_0: p = 0.75, H_1: p!=0.75
1-PropZTest: z = 2.73, p-value = 0.0064
Reject H0
There is sufficient evidence to warrant rejection of the claim that the percentage of adults who think it is morally wrong to not report all income on tax returns is 75%.
100
Based on the data from six students, the regression equation relating number of hours of preparation (x) and test score (y) is y = 67.3 + 1.07x. The same data yield r = 0.224 and
bary=75.2
What is the best predicted test score for a student who spent 3 hours preparing for the test?
75.2
200
A group of recent high school graduates were randomly selected and asked whether they planned to vote in the next election. The results are shown below. Use a 0.05 significance level to test for independence between gender and voting plans.
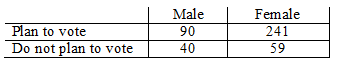
H0: Gender is independent of whether a person votes.
H1: Gender is dependent on whether a person votes.
chi^2-Test: chi^2=6.31
p-value = 0.01
Reject H0
There is sufficient evidence to warrant rejection of the claim that gender is independent of voting plans.
The evidence shows that whether a person votes is dependent on gender.
200
The following data are x = average on five quizzes prior to the midterm exam and y = score on the midterm exam for eleven students randomly selected from a statistics class of about 950 students.
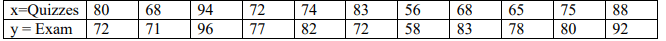a. Is there significant correlation?
b. Calculate the regression line for this equation.
c. What is the predicted midterm exam score for a student with a quiz average equal to 75?
a) Yes, there is significant linear correlation.
b) y = 25.38 + 0.707x
c) 78.4
200
The times of sleep for randomly selected adult subjects are listed below.
4 5 4 4 8 6 9 7 7 6 7 8
a. Test the claim that the mean number of hours of sleep is less than 8 hours.
b. If eight hours of sleep is considered ideal, what do the results indicate?
H_0: mu=8, H_1:mu<8
T-Test: t = -3.54, p-value = 0.0023
Reject H0
There is sufficient evidence to support the claim that the mean hours of sleep is less than 8.
b) Sleep amounts are less that ideal since they are significantly less than 8.
300
160 students who were majoring in either math or English were asked a test question, and the researcher recorded whether they answered the question correctly. The sample results are given below. At the 0.10 significance level, test the claim that responses and major are independent.
300
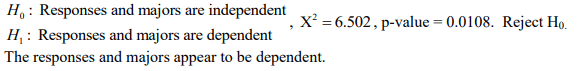
At the 0.025 significance level, test the claim that the four brands have the same mean volume if the following sample results have been obtained.
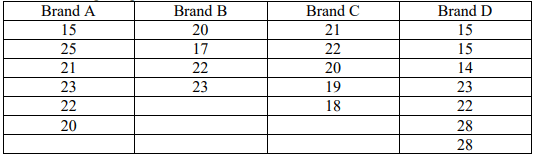
H_0:mu_1=mu_2=mu_3=mu_4
H1: At least one of the means is different.
ANOVA: F = 0.055, p-value = 0.982
Fail to reject H0
There is not enough evidence to reject the claim of equal means. The means appear to be equal.
300
In testing a new vaccine for shingles, 43 of 900 people vaccinated later developed the disease. 86 of 1000 people vaccinated with a placebo later developed the disease. Use a 0.05 significance level to test the claim that a higher proportion of people with the placebo develop the disease.
H_0:p_1=p_2, H_1:p_1<p_2
2-PropZTest: z = -3.31, p-value = 0
Reject H0
There is sufficient evidence to support the claim that people are more likely to get shingles if they are unvaccinated.
400
The summary statistics for the ages of actresses when they won Oscars are n = 87
barx=36.2
years, and s = 11.5 years. Use a 0.10 significance level to test the claim that the mean age of actresses when they win Oscars is greater than 30 years.
H_0:mu=30,H_1:mu>30
T-Test: t = 5.03, p-value = 0.0000013
Reject H0
There is sufficient evidence to support the claim that the mean age is greater than 30.
400
The data below gives the weights (in pounds) of 9 basketball players on each of the local community college and university teams. Test the hypothesis (at the 0.05 level) that the mean weights of basketball players on the community college and university basketball teams are different.
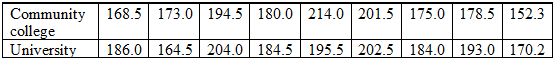
H_0:mu_1=mu_2
H_1:mu_1!=mu_2
2-SampTTest: t = -0.68, p-value = 0.5064
Fail to reject H0
There is not sufficient evidence to support the claim that the mean weights of basketball players on the community college and university basketball teams are different.
400
Researchers collected a simple random sample of the times that 81 college students required to earn their bachelor’s degrees. The sample has a mean of 4.8 years and a standard deviation of 2.2 years. Use a 0.05 significance level to test the claim that the
mean time for all college students is different than 4.5 years.
H_0:mu=4.5, H_1: mu!=4.5
T-Test: t = 1.23, p-value = 0.2233
Fail to reject H0
There is not sufficient evidence to support the claim that the mean time is different than 4.5 years.