Ch.6 Applications of Integrals
Ch.7 Techniques of Integration
Ch.8 Further Applications of Integration
Ch.9 Differential Equations
Ch.11 Sequences, Series and Power Series
100
Find the volume of the region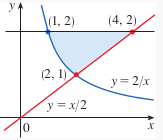
about the y-axis.
\frac{22\pi}{3}
100
\int xe^{2x} dx
\frac1 2 xe^{2x}- \frac1 4 e^{2x}+C
100
Find the center of mass given
m_1=5,m_2=8,m_3=7, \quad (3,1),(0,4),(-5,-2)
(-1,\frac23 20)
100
y=\sqrt x
a solution for
xy'-y=0
No
100
The series
\sum_{n=1}^\infty \frac{1}{n^3}
converges or diverges?
Converges. (p-series)
200
Find the area of the given region by
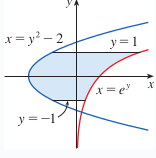
e-(\frac{1}{e})+\frac10 3
200
\int sin^5(2t)cos^2(2t)dt
-\frac1 14 cos^7(2t)+ \frac1 5 cos^5(2t)- \frac1 6 cos^3(2t) +C
200
Find the arc length of
y=\frac{1}{2}ln(sin(2x)), \quad \pi/8 \leq x \leq \pi/6
\frac1 2 [\ln(\frac{1}{\sqrt{3}})-\ln(\sqrt{2}-1)]
200
Find the general solution for
\frac{dy}{dx}=3x^2y^2
y=\frac{-1}{x^3+C}
200
The series
\sum_{n=2}^\infty \frac{1}{n (\ln n)^3}
converges or diverges?
Converges. (integral test)
300
Find the volume of the region bounded by
y=\sqrt{5+x^2},\quad y=0,\quad x=0,\quad x=2
about the y-axis
\frac{2}{3}pi(27-5\sqrt 5)
300
\int \frac{5x+1}{(2x+1)(x-1)}dx
\frac1 2 ln|2x+1|+2 ln|x-1|+C
300
Find the arc length of
x=sin(y), \quad 0 \leq y \leq \pi/2
1
300
Find the general solution for
\frac{dp}{dt}=t^2p-p+t^2-1
y=Ce^{\frac{1}{3}t^3-t}-1
300
The series
\sum_{n=1}^\infty (-1)^n \frac{1}{\sqrt{n^2-9}}
is absolutely convergent, conditionally convergent or divergent?
Converges absolutely (Alternating Series Test)
400
Find the volume of the region bounded by
x=2y^2, \quad y \geq 0, \quad x=2
about y=-2
\frac{13pi}{3}
400
\int_3^\infty \frac{1}{(x-2)^{3/2}}dx
2
400
Find the center of mass of
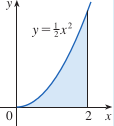
(\frac3 2 ,\frac3 5 )
400
Find the specific solution for
\frac{dy}{dx}=xe^y, \quad y(0)=0
y=-\ln(1-\frac1 2 x^2)
400
The series
\sum_{n=1}^\infty \frac{n!}{100^n}
converges or diverges?
Diverges. (Ratio Test)
500
Find the volume of the region bounded by
y=\sin(x), \quad y=cos(x), \quad 0 \leq x \leq \pi/4
about y=-1.
\pi(2\sqrt{2}-\frac3 2)
500
\int \frac{\sqrt{4x^2-25}}{x}dx
\sqrt{4x^2-25}-5sec^{-1}(\frac2 5 x)+C
500
Find the center of mass of the region
ysin(2x), \quad y=sin(x), \quad 0 \leq x \leq pi/3
(pi-3/2\sqrt(3),3/8\sqrt(3))
500
Find the specific solution for
\frac{du}{dt}=\frac{2t+sec^2t}{2u}, \quad u(0)=-5
u=-\sqrt{t^2+tan t+25}
500
What is the Taylor series for
f(x)=\frac{1}{1+x}
centered at a=2.
\sum_{n=0}^\infty (-1)^n \frac{1}{3^{n+1}}(x-2)^n