Sequences
Area and Solving Equations
Properties of Exponents
Percent Problems
100
Determine if the sequence is arithmetic or geometric, then find the explicit formula.
-2, -8, -32, -128, ...
Geometric
t(n)=(-1/2)4ⁿ
100
Write the area as a sum equal to the area as a product.
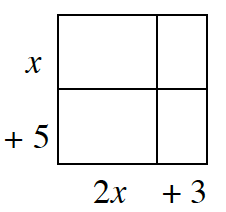
(x+5)(2x+3)=2x2+13x+15
100
Simplify the expression 3x2x6
3x8
100
Determine whether the geometric sequence represents growth or decay. (Hint: what kind of number is the multiplier?)
t(n)=1.50(0.8)^n
Decay because the multiplier is between 0 and 1.
200
Determine if the sequence is arithmetic or geometric, then find the explicit equation.
7, 5, 3, 1, -1, ...
Arithmetic
t(n)=-2n+9
200
Write the area as a sum equal to the area as a product.
x^2-5x+6=(x-2)(x-3)
200
Simplify the following expression.
(6n^9)/(3n^5)
2n^4
200
Convert the percent decrease into a multiplier:
30% decrease
0.70
300
What is the 10th term for the sequence below?
15, 5, 5/3, ....
t(n)=45(1/3)^n
t(10)=45(1/3)^10=0.00076
300
Solve the equation for x:
(2x+3)(x-1)=x(2x+5)
x=-3/4
300
Simplify the expression:
(–3xy^2)^2 (–2x^2y)
-18x^4y^5
300
A population increases on average by 2.2% per year. If the starting population is 12,010, what is the population after 3 years?
12,820 people