Identify the slope (change) for the following equation:
y = -1/2x + 12
-1/2
Write the product as a sum. Use the area model to solve.
(2x - 1)(x + 3)
(2x-1)(x + 3) = 2x^2 + 5x -3
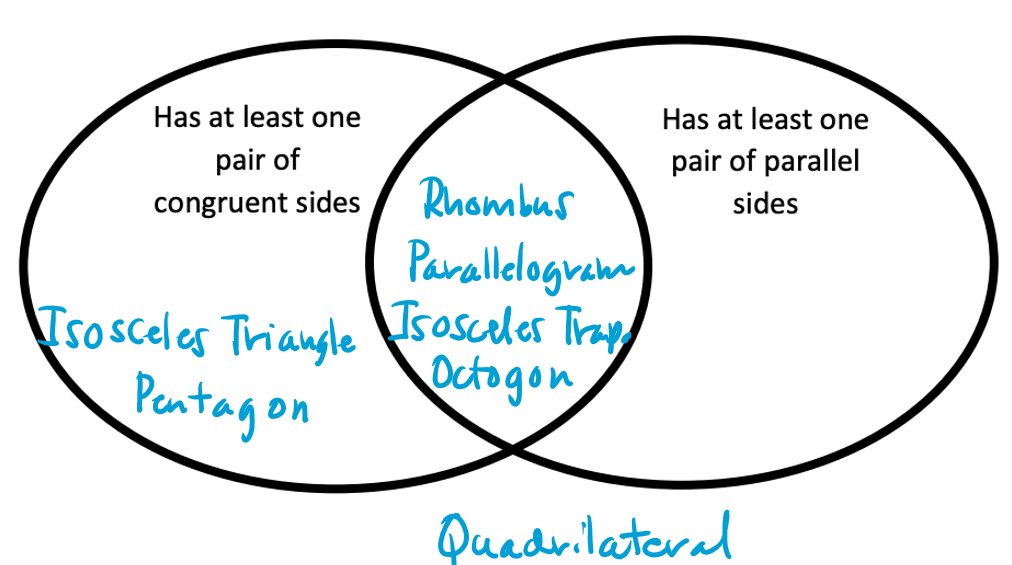
Where in the Venn Diagram would a square be classified?
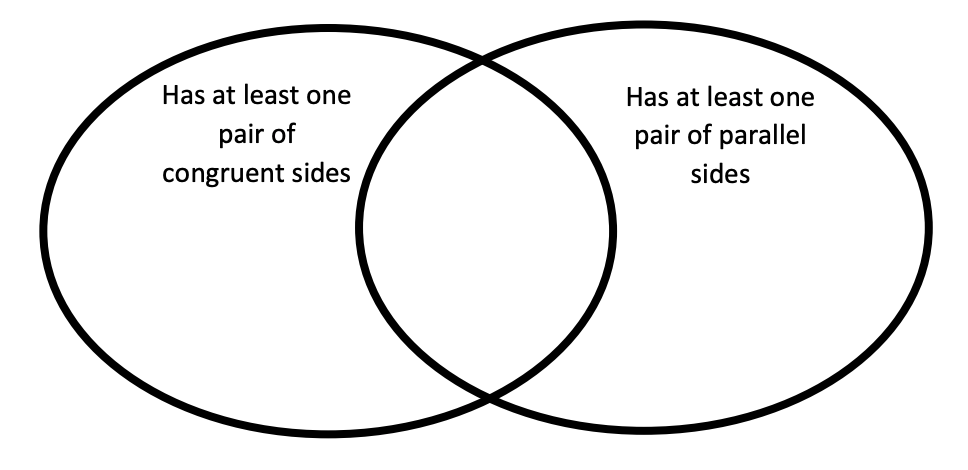
In the middle.
Name the 3 transformations below in the order they appear.
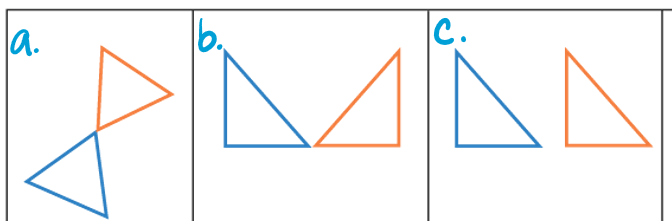
a. Rotation
b. Reflection
c. Translation
Write the general equation for a linear equation and an exponential equation. Label the Linear equation with an "L" and the exponential equation with an "E".
L (y = mx+b)
E (y = ab^x)
Given the table, write a linear equation that models the information.
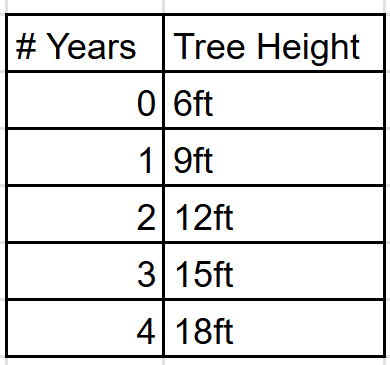
y = 3x + 6
Write the following product as a sum.
(3x - 5)^2
(3x - 5)^2
(3x-5)(3x-5) = 9x^2-30x+25)
Where in the following Venn Diagram would a trapezoid be classified?
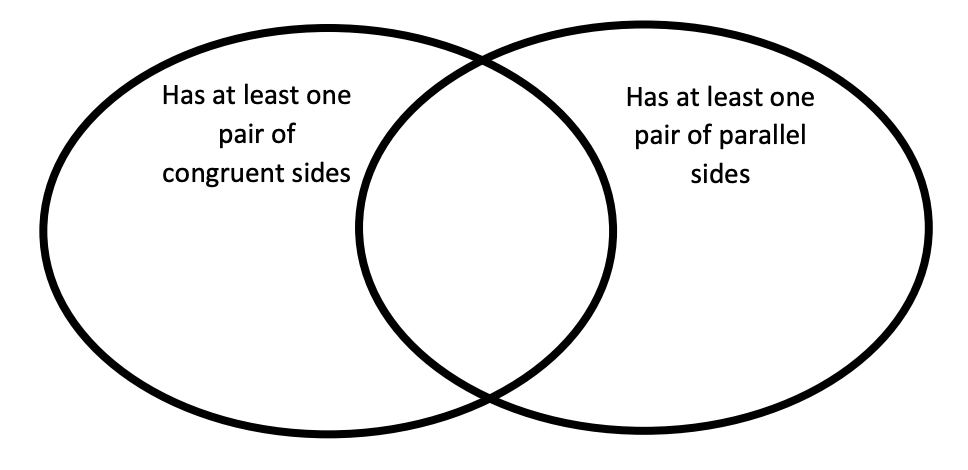
In the circle with at least one pair of parallel sides.
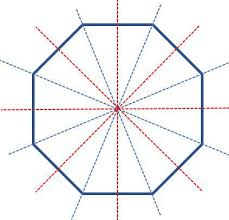
True or False. An octogon has reflection symmetry.
True
For the following tables, determine which one is linear and which one is exponential.
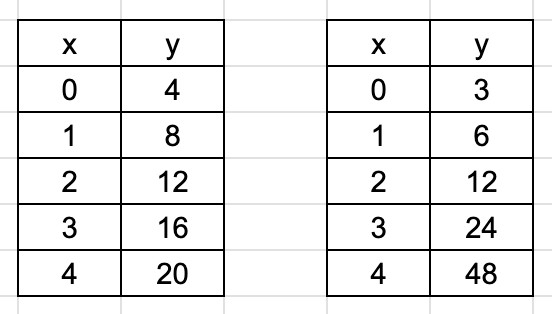
y = 100x + 450
Fill in the missing values to write the product as a sum:

(3x + 5)(x + 2) = 3x^2+11x + 10
For the following Venn Diagram, how would an Isosceles Triangle be classified?
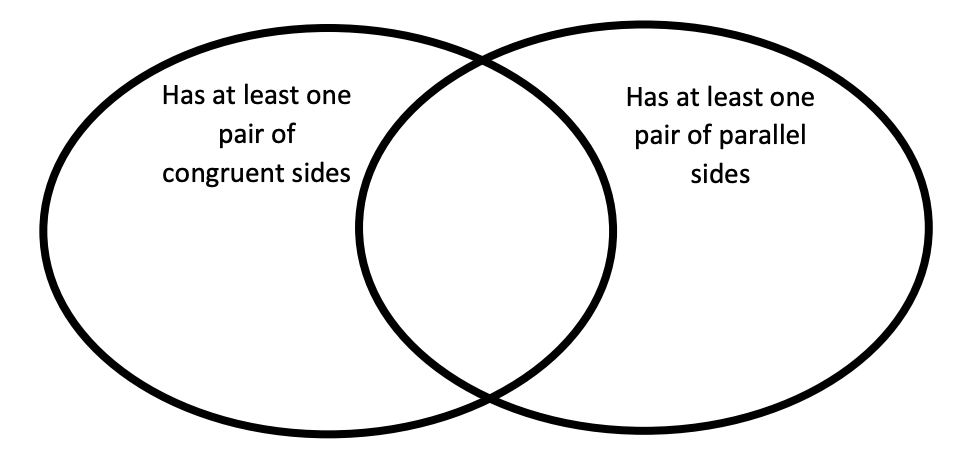
In the circle with "has at least one pair of congruent sides".
Give two reasons as to how you know the image represents a translation.
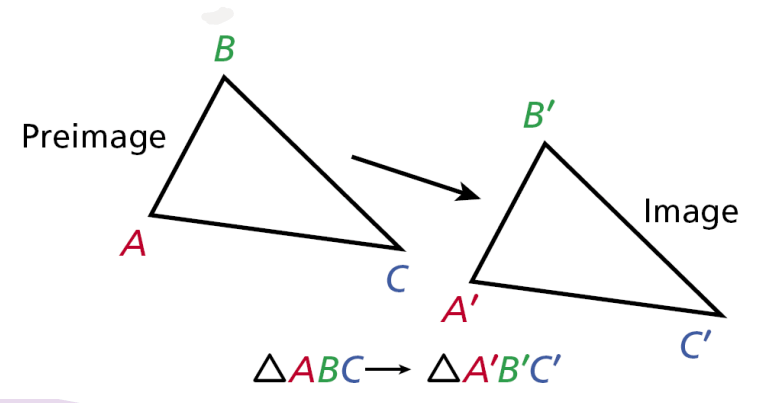
1. The image "shifted" or "moved" right without changing orientation, size, or shape.
2. The new figure(triangle) uses prime notation.
Write an exponential equation that represents a car's purchase price at $45,000 that depreciates at a rate of 22% each year.
y = $45,000(.78)^x
Josiah begins 1st period with 100 pieces of candy. His classmates find out about his candy and he shares his candy at a rate of 2 pieces per second. Write a linear equation to model the scenario.
y = -2x + 100
Use the area model to write the product as a sum.
(3x - 8)(x^2 + 4x -10)
(3x - 8)(x^2 + 4x -10) = 3x^3+4x^2-62x + 80
Which statement is TRUE.
A. All quadrilaterals are rectangles, but not all rectangles are quadrilaterals.
B. All rectangles are quadrilaterals, but not all quadrilaterals are rectangles.
Answer B
If point B(10, -7) translates 6 left and 4 up, what are the new coordinates for B' ?
10 - 6 = 4 (x)
-7 + 4 = -3 (y)
B' (4, -3)
If an investment is worth $300 and 12% interest each year, what will the investment be worth in 8 years? Round your answer to the nearest penny.
Equation:
y = $300(1.12)^8
Answer = $742.79
Part A: If Josiah has 100 pieces of candy and gives them away at a rate of 2 pieces per second. How much candy will he have left at 30 seconds.
Part B: If Josiah only has 4 pieces of candy remaining, how many seconds did it take?
Part A: y = -2(30) + 100
y = 40 pieces of candy
Part B: y = -2x + 100
4 = -2x + 100
x = 48 seconds
Fill in the missing information and then write the product as a sum.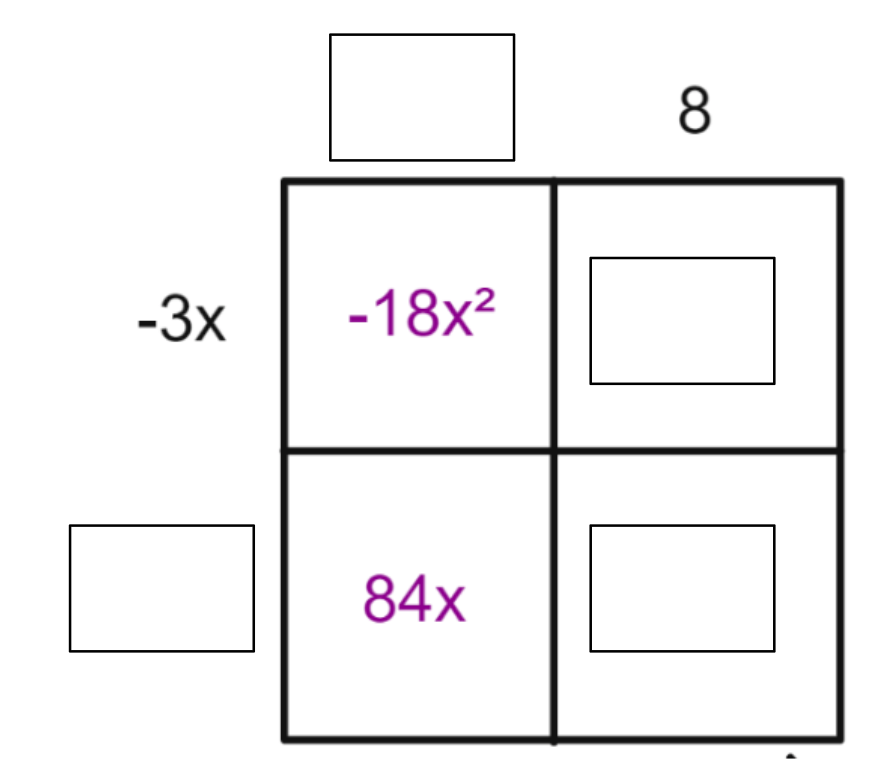
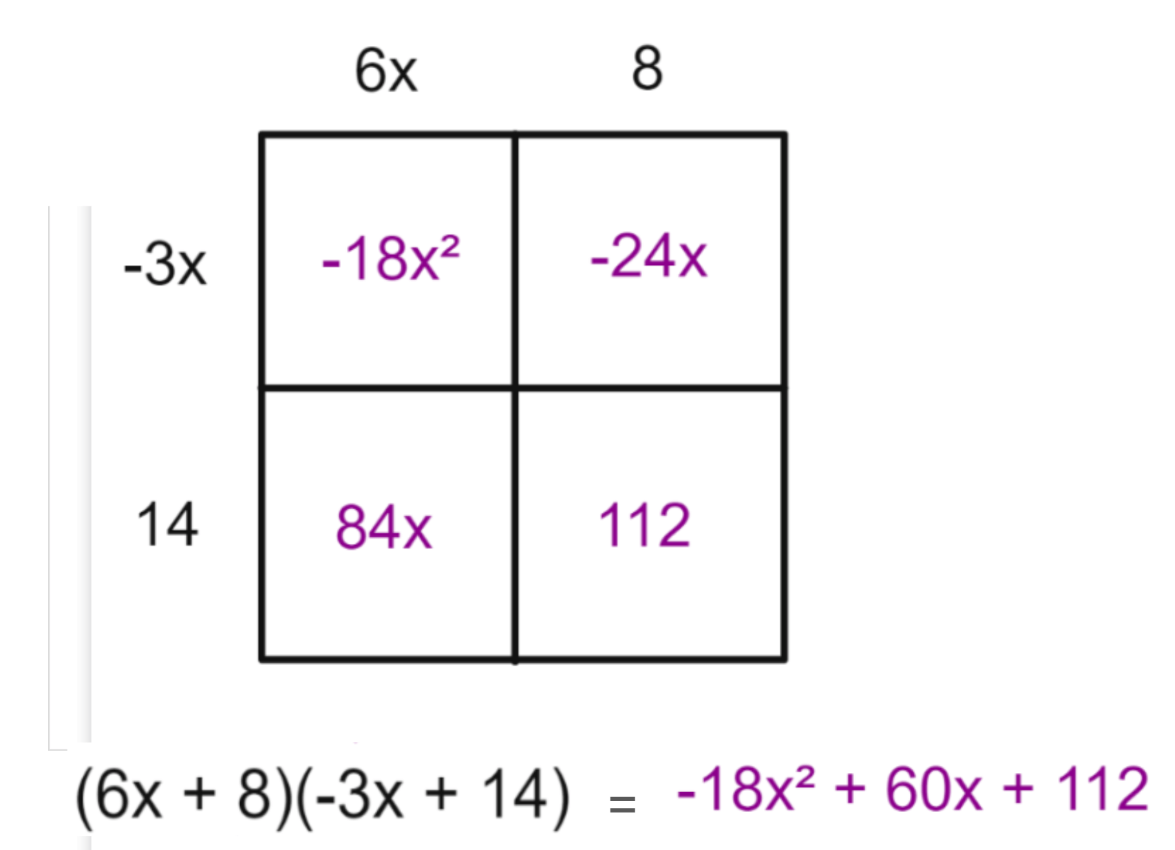
Write down all errors you find and re-classify them by drawing the correct Venn Diagram.
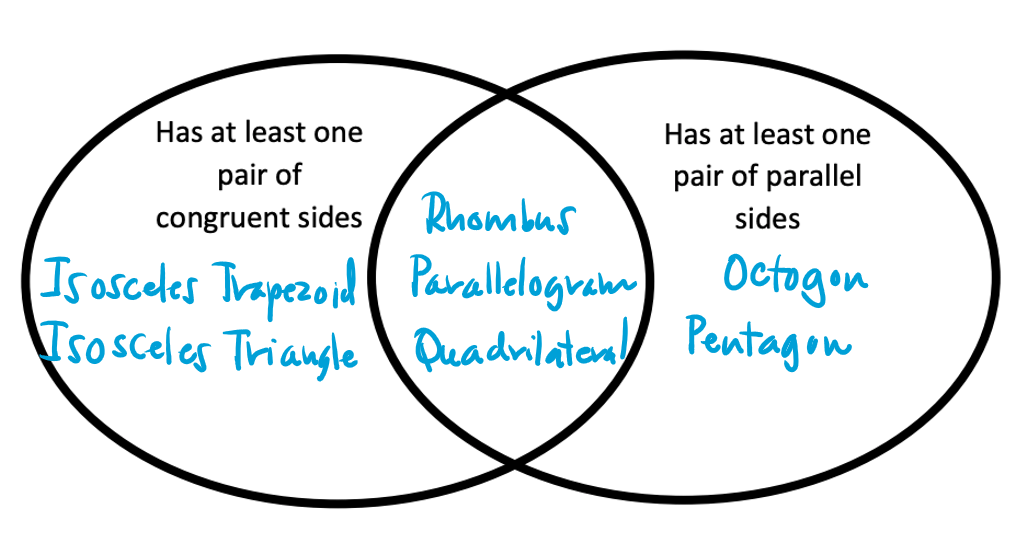
Correct Venn Diagram
A line with points A(-7, 5) and B(9, -6) is rotated 180 degrees about the origin. What are the lines new coordinates? Rule existing (x,y) >>>> (-x, -y).
A (-(-7), -5) = A' (7, - 5)
B (-9, -(-6)) = B' (-9, 6)
A medication has an initial concentration of 200 mg in the bloodstream and is decreasing by a certain percentage per hour. If after 2 hours, the concentration is 50 mg. What is the percent decrease? (Hint: solve for b).
50 = 200(b)^2
Divide both sides of the equation by 200 to isolate b^2. To isolate b take the square root of each side of the equation. Answer is .50 which is 50%.