Implication of Word Problems
Derivatives
Limits
Extra Word Problem
100
State the equation for a revenue function R(x) as well as the equations for P(x) and C(x). Use q for demand, p for price, and x for the amount of units.
P(x) = R(x) - C(x)
R(x) = (q)(p)
C(x) = (c)(q)+f
100
Find the equation of a line which passes through points (2,6) and (5,-12)
F(x)=mx+b
M=(-12-6)/(5-2)
=-18/3
M=-6
So, 6=(-6)2+b
18=b
F(x)=-6x+18
100
What 3 conditions are needed for a limit to exist?
1. Lim x -> a^-
Must exist
2. Lim x -> a^+
Must exist
3. Both limits must equal each other
100
x^2+2x-8
represents the profit generated by dog toy sales in thousands of dollars at x hundred units sold.
Find the percent rate of change at x=3 (round to nearest percent) and interpret your answer. What would the units be on f'(3)?
PRC = 114% -> This means that selling 400 units would increase profits by 114%
The units would be thousands of dollars per 100 units
200
Define the practical domain for a company using a new mechanism to remove a certain percentage of carbon emissions from their factories.
You can't have negative emissions, so
(0,100)
200
What derivative rules are required to solve this problem and what order would they be used in?
Bonus points to solve!
F(x)=5x^3-7x^2+9
Power rule, followed by addition/subtraction rule
15x^2-14x
200
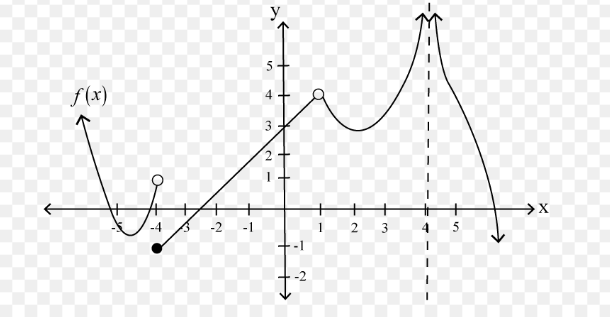
a. Lim F(x) x->-4^-
b. Lim F(x) x->-4^+
c. Lim F(x) x->4
a. 1
b. -1
c. infinity
300
The function f(a) represents the taxable income (in thousands of dollars) for an
individual with federal tax rate a (as a percentage). The equation f(5) = 20 means...
An individual with a taxable income of 20 thousand dollars has a federal tax rate of 5%
300
Find the average rate of change for the following table on the interval [-1,4]
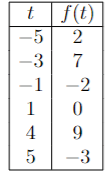
ARC=(f(4)-f(-1))/(4-(-1))
(9-(-2))/5
11/5
300
(x^4-2x^3+6x)/(2x^3-4)
Find the
Lim F(x) x->3
((3)^4-2(3)^3+6(3))/((2(3)^3)-4)
9/10
400
A company's profit is represented by the function
P(x)=-x^2+980x-3000
When is profit at its maximum? What is the maximum profit?
Max occurs at x=490.
So
P(490)
is the max profit
400
Suppose that for two differentiable functions f and g, we know that f ′(2) =9 and g′(2) = 12. What is the value of h′(2), if h(x) = 5f(x)−g(x)?
5f'(x)-g'(x)
h'(2)=5f'(2)-g'(2)
=5(9)-12
33
400
Determine whether or not the function is continuous for all real numbers
F(x)={x+3, if x<1
F(x)={x^3-x+4, if x>=1
F(1)=(1)^3-(1)+4=4
Lim x->1^-)=(1)+3=4
Lim x->1^+)=(1)^3-(1)+4=4
F(x) is continuous for all real numbers
500
Identify the break-even point, given a demand of q = 72 − 3p items produced when charging p dollars per item, and total cost C = 5q dollars.
Which answer makes sense given the context?
The break-even point occurs when 57 items are produced and sold at $5 each.
500
Find the derivative of
f(x) = x^2+5
using the limit definition of a derivative
lim_(h->0) (f(x+h)-f(x))/h
f'(x) = 2x
500
The limit as x approaches infinity
(2x^4-9x^3+2x)/(4x^4-3x^3+7x+2
(((2x^4)/x^4)-((9x^3)/x^4)+((2x)/x^4))/(((4x^4)/x^4)-((3x^3)/x^4)+((7x)/x^4)+((2)/x^4))
2/4=1/2