Solving Linear DEs (Pt 1)
Solving Linear DEs (Pt 2)
Mixing Problems
RREF and Elementary Row Operations
Matrix Operations
100
What is the starting equation/preparation to solve a DE using the integrating factor.
dy/dx + p(x)y = q(x)
100
What are the 3 steps for separation of variables.
1. Separate
2. Integrate
3. Solve for y (if possible)
100
In a mixing problem, interpret dV/dt, dA/dt, v(t), A(t), and c(t) in real world context.
dV/dt = rate of change of volume over time t
dA/dt = rate of change of sugar in the fluid over time t
v(t) = volume of liquid in tank @ time t
A(t) = amount of sugar in tank @ time t
c(t) = ratio of sugar in the tank to volume of liquid in the tank (concentration)
100
List the three Elementary Row Operations you can perform on a matrix to get to RREF.
1. Swap any pair of equations
2. Add any multiple of one row to another
3. Scale an equation by a nonzero number
100
Scale matrix A by -4.
A = [[-2,1,0],[4,1/2,6],[0,3,-1]]
(-4)A = [[8,-4,0],[-16,-2,24],[0,-12,4]]
200
Complete the general equations for using the integrating factor:
I(x) =
y =
I(x) = e^(intp(x)dx)
y = 1/(I(x))*intI(x) q(x) dx
200
Test if this equation can be solved using V-sub:
dy/dx = (y+xe^(y/x))/x
y = ty
x = tx
(ty+txe^((ty)/(tx)))/(tx) = (t(y+xe^(y/x)))/(t(x)) = (y+xe^(y/x))/x
200
A tank initially contains 10 L of liquid in which 25 grams of sugar are dissolved. A sugar-water solution flows into the tank at a rate of 5 L/m and has a sugar concentration of 3 g/L. The mixture is constantly stirred and flows out at a rate of 3 L/m. Find the equation for volume.
v(t) = 2t + 10
200
Write this system of equations in the three other notations and label them.
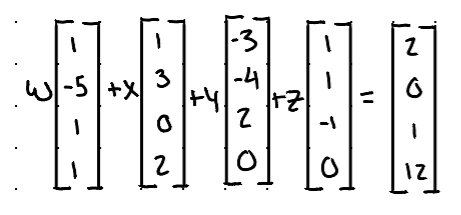
w + x - 3y + z = 2
-5w + 3x - 4y + z = 0
w + 2y - z = 1
w + 2x = 12
Matrix-Vector Equation: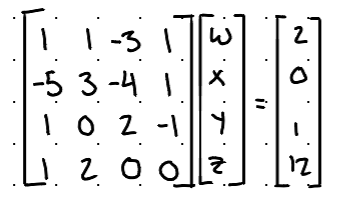
Vector Equation:
Augmented Matrix Notation:
200
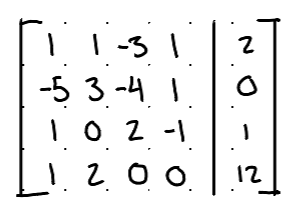
Complete the following matrix arithmetic, A - B + C
A = [[3,5,0],[1,6,1],[-6,-3,-8]]
B = [[-2,-5,9],[3,-3,3],[-6,-2,2]]
C = [[2,7,4],[-7,8,-2],[-4,-7,2]]
A - B + C = [[7,17,-5],[-9,1,-4],[-4,-8,-8]]
300
y'' - 2y' + y = 0
Prove y(x) = xe^x is a solution.
y = xe^x
y' = xe^x + e^x
y'' = xe^x + 2e^x
xe^x + 2e^x - 2(xe^x + e^x) + xe^x = 0
0 = 0. So y = xe^x is a solution.
300
Complete the substitutions for V substitution.
dy/dx =
y =
dy/dx = V + x(dV)/dx
y = Vx
300
A tank initially contains 10 L of liquid in which 25 grams of sugar are dissolved. A sugar-water solution flows into the tank at a rate of 5 L/m and has a sugar concentration of 3 g/L. The mixture is constantly stirred and flows out at a rate of 3 L/m. Find the equation for amount of sugar.
A(t) = 6/(t+10)^2 * (1/3 t^3 + 10t^2 + 100t + C)
300
Find the matrices that are in Row Reduced Echelon Form.
[[1,0,0,2],[0,1,0,2],[0,0,1,-1]]
[[6,0,1,0,0],[0,0,0,1,0],[0,-1,0,0,1]]
[[1,0,4,2,0,1],[0,1,-1,3,0,2],[0,0,0,0,0,0]]
[[1,0,3,0,-4],[0,1,-7,1,0],[0,0,0,1,-1]]
[[0,0,0,0],[0,0,0,0],[0,0,0,0]]
[[1,0,-15,0,-30],[0,1,7,0,14],[0,0,0,1,-1]]
[[1,-4,0,8],[0,0,0,0],[0,0,1,2]]
Is in RREF:
[[1,0,0,2],[0,1,0,2],[0,0,1,-1]]
[[1,0,4,2,0,1],[0,1,-1,3,0,2],[0,0,0,0,0,0]]
[[0,0,0,0],[0,0,0,0],[0,0,0,0]]
[[1,0,-15,0,-30],[0,1,7,0,14],[0,0,0,1,-1]]
Is NOT in RREf:
[[6,0,1,0,0],[0,0,0,1,0],[0,-1,0,0,1]]
[[1,0,3,0,-4],[0,1,-7,1,0],[0,0,0,1,-1]]
[[1,-4,0,8],[0,0,0,0],[0,0,1,2]]
300
Find the statement that is true when multiplying matrices A*B.
1) The number of rows in matrix A must equal the number of columns in matrix B.
2) The number of columns in matrix A must equal the number of rows in matrix B.
2) The number of columns in matrix A must equal the number of rows in matrix B.
EX: 2 x 3 and 3 x 2
400
Solve using the integrating factor:
dy/dx - 4y = e^(5x)
y = e^(5x) + Ce^(4x)
400
Use separation of variables to find the explicit solution of this differential equation:
x^2 + 4 - y^3(dy)/dx = 0
y = (4/3x^3 + 16x + C)^(1/4)
400
v(t) = t + 10
A(t) = 6/(t+10)^2 * (1/3 t^3 + 10t^2 + 100t + 200)
Vat capacity = 20 L
Find the amount of sugar at tank capacity.
A(10) = 38 g
400
List the pivot variables and the free variables from this matrix in RREF, then organize into parametric vector form.
[[1,0,-3,0,9],[0,1,7,0,-4],[0,0,0,1,11]][[12],[18],[-13]]
Pivot Variables: x1 , x2 , x4
Free Variables: x3 , x5
[[x1],[x2],[x3],[x4],[x5]]=[[12],[18],[0],[-13],[0]]+x3[[3],[-7],[1],[0],[0]]+x5[[-9],[4],[0],[-11],[1]]
400
Find A*B by multiplying the matrices, if possible.
A = [[-5,5,-4],[-2,2,2]]
B = [[-3,-6],[2,3],[6,1]]
A*B = [[1,41],[22,20]]
500
Determine which method you would use to solve these DEs.
1. y′=(x2+1)y
2. (x+1)y′−y=x
3. y′=(y+2x)/x
1. Separation of Variables
2. Integrating Factor (Linear)
3. Change of Variable (V = y/x)
500
Use V substitution to find the implicit solution to this differential equation:
x(dy)/dx = y + xe^(y/x)
-e^(-y/x) = ln|x| + C
500
v(t) = t + 10
A(t) = 6/(t+10)^2 * (1/3 t^3 + 10t^2 + 100t + 200)
Find the concentration, c(t).
c(t) = [6(1/3 t^3 + 10t^2 + 100t + 200)]/[(t+10)^3]
500
Find inverse, A-1 of matrix A using RREF.
A = [[1,5,9],[3,7,2],[0,1,3]]
A^-1 = [[19,-6,-53],[-9,3,25],[3,-1,-8]]
500
Calculate A*B - B*A using the given matrices.
A = [[2,4],[-3,5]]
B = [[-1,-2],[3,-3]]
A*B - B*A = [[6,-2],[3,-6]]