Unit 1
Unit 2
Unit 3
Unit 4
Additional ?'s
100
Express the Domain of the following graph in:
a) Inequality Notation
b) Interval Notation
a) x ≤ -1
b) (-∞,-1]
100
Simplify
sqrt(16y^2x^6)
4yx3
100
Find the AOS, domain, range, and vertex of the function:
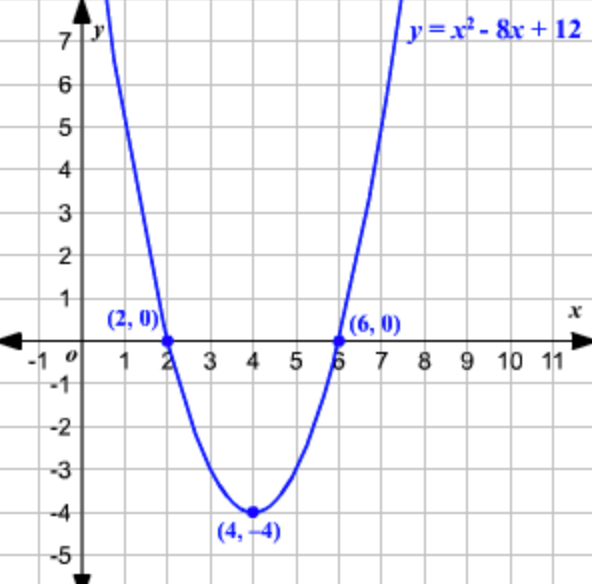
AOS: x = 4
Domain: (-∞,∞)
Range: [-4,∞)
Vertex: (4,-4)
100
Solve by factoring:
x^2-x-12=0
x=4 and x=-3
100
Subtract
(4-7i)-(5+2i)
-1-9i
200
List the transformations:
y=-1/3abs(x+2)-5
Reflect, VC, Left 2, Down 5
200
Simplify
(3m^(8))*(-9m^(5))
-27m13
200
What are the solutions for the following quadratic: (x-9)(2x+1)=0
x=9 and x=-1/2 or -.5
200
Use the quadratic formula to solve the following:
2x^2-5x+1
x=(5+-sqrt(17))/4
200
Multiply
(4-7i)(5+2i)
34 - 27i
300
Write the equation for the following graph:
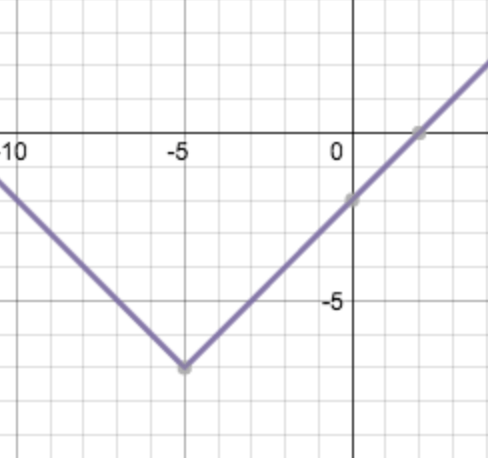
y = |x + 5| - 7
300
Write the radical in rational exponent form:
sqrt(p^7)
p^(7/2)
300
Describe the transformations for the following quadratic and find the vertex:
y=-2(x-4)^2+9
Reflection, Vertical Stretch(Skinnier), Right 4, Up 9
Vertex is (4,9)
300
Factor: 9x2 - 100
(3x - 10)(3x + 10)
300
Find the vertex of y = x2 -10x + 25
(5,0)
400
Solve 3|x - 4| +7 = 13
x = 2 and x = 6
400
Multiply
(x-3)(x2+8x-4)
x3+5x2-28x+12
400
A fish jumps out of water. The function
h(t) =
-16t^2+24t
models the height, in feet, of the fish above water after t seconds. How long is the fish out of water? (Round to the nearest tenth of a second)
1.5 seconds
400
Factor completely:
4x2 + 2x - 12
2(2x-3)(x+2)
400
Solve 3|3x - 4| +7 = 1
No Solution (absolute value can not equal a negative after you isolate it)
500
Find the solutions to the following absolute value inequality: |x-3| - 5 < 1
(less thAND type problem)
Solution: -3 < x < 9
500
Simplify
(5x-4)^2
25x^2-40x+16
500
Find the zeros for the following function (Solve using the quadratic formula)
f(x)=x^2-3x-6
x=(3+-sqrt(33))/2
500
Solve
81x^2+49=0
x=-7/9i and x=7/9i