Domain, Range, Characteristics
Absolute Value Inequalities
Absolute Value Equations
More Absolute Values
100
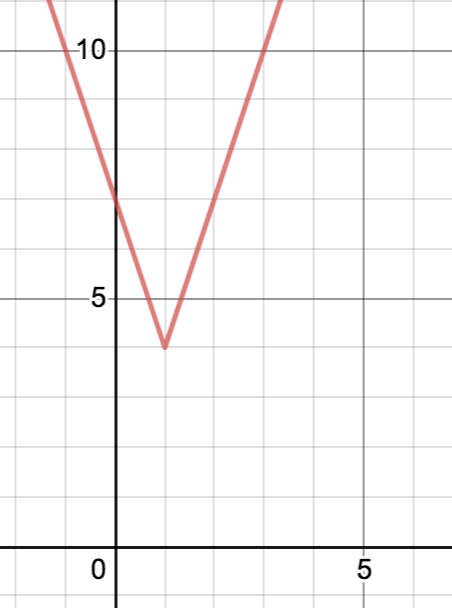
a) What is the domain and range of the following diagram in inequality notation?
b) If you restrict the domain from 0≤x≤2 what is the range in inequality notation?
What is a) Domain: -∞<x<∞, Range: -∞<y<∞
b) Range: -2≤y≤2
100
Solve Algebracially: 3|x| + 2 < 11
What is -3<x<3
100
Describe the transformations from f(x) = |x| to g(x) = (1/2)|x+2| - 5.
What is g(x) is down 5, compressed vertically, and to the left 2 from f(x)
100
Write the equation of an absolute value that is translated down 4 and left 2.
What is y = |x+2| - 4
200
Write the range of the following graph in inequality notation.
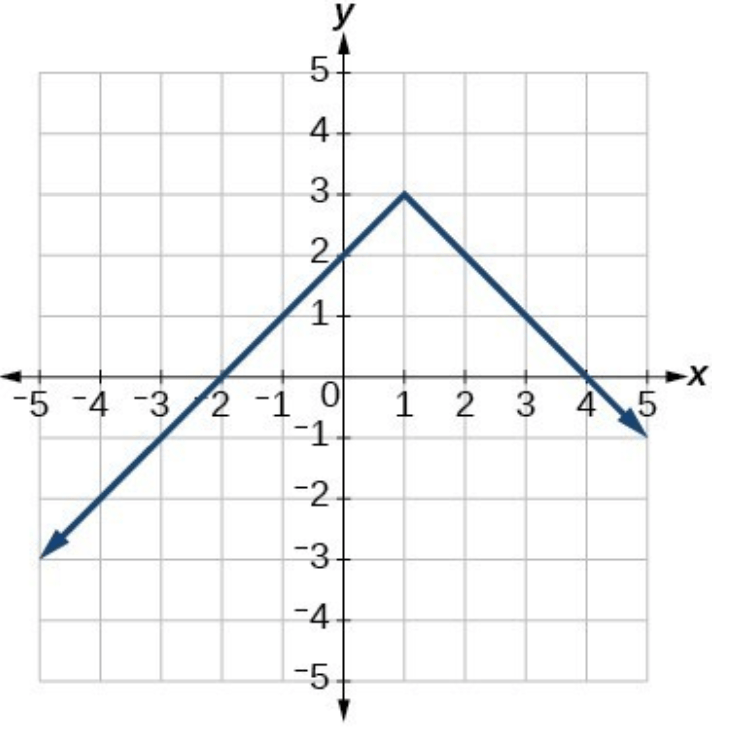
What is y≤3
200
Solve By Algebraically
3|x-4|+2>8
What is x>6 or x<2? (OR problem)
200
Write the function that represents the graph and write the range in inequality notation.
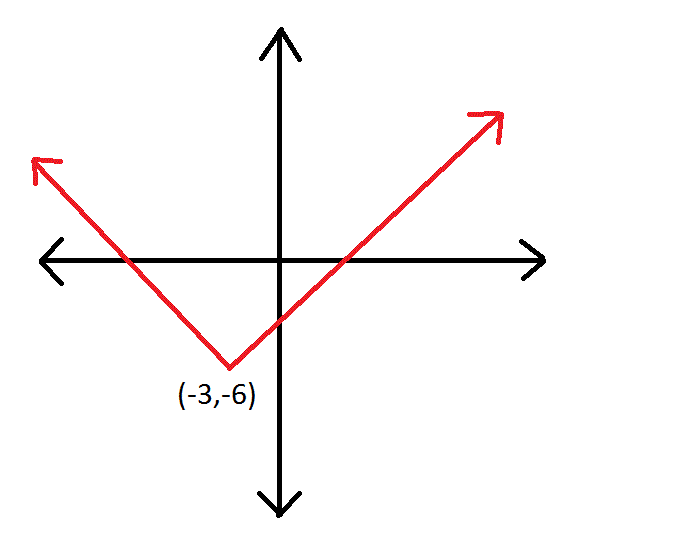
What is f(x) = |x+3|-6 and the range in inequality notation is y≥-6
200
Solve the following absolute value equation algebraically:
1/2abs(2x+5)+10=6
What is No Solution?
300
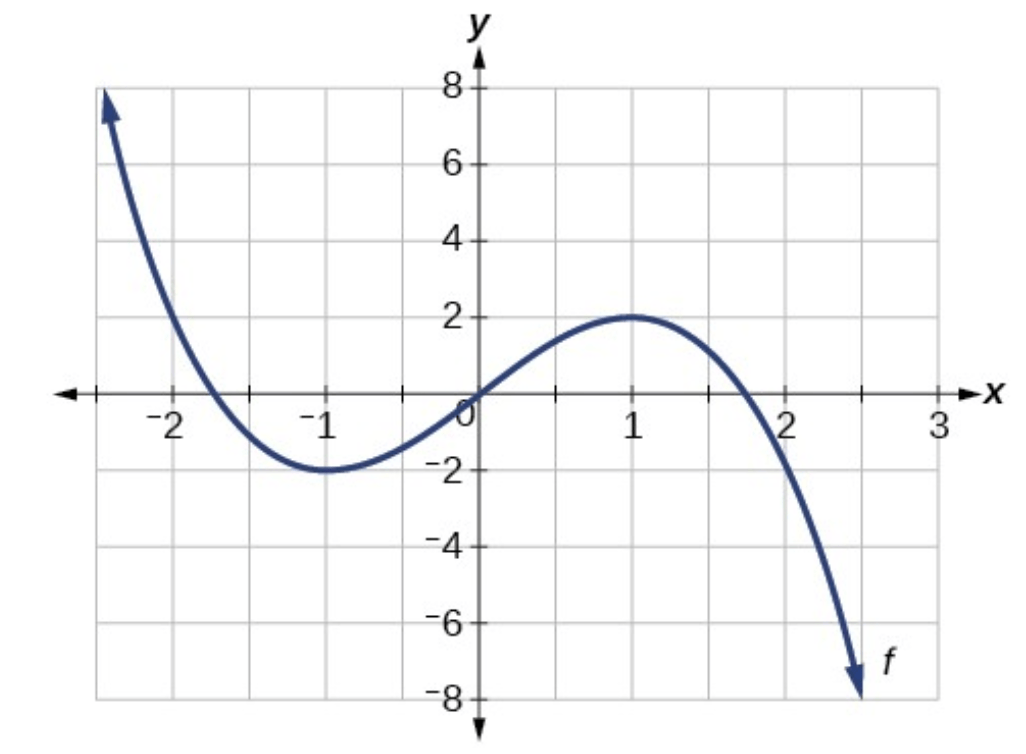
a) What is the rate of change on the interval 5<x<7?
b) List the zeros (coordinates)
c) List the y-intercept (coordinate)
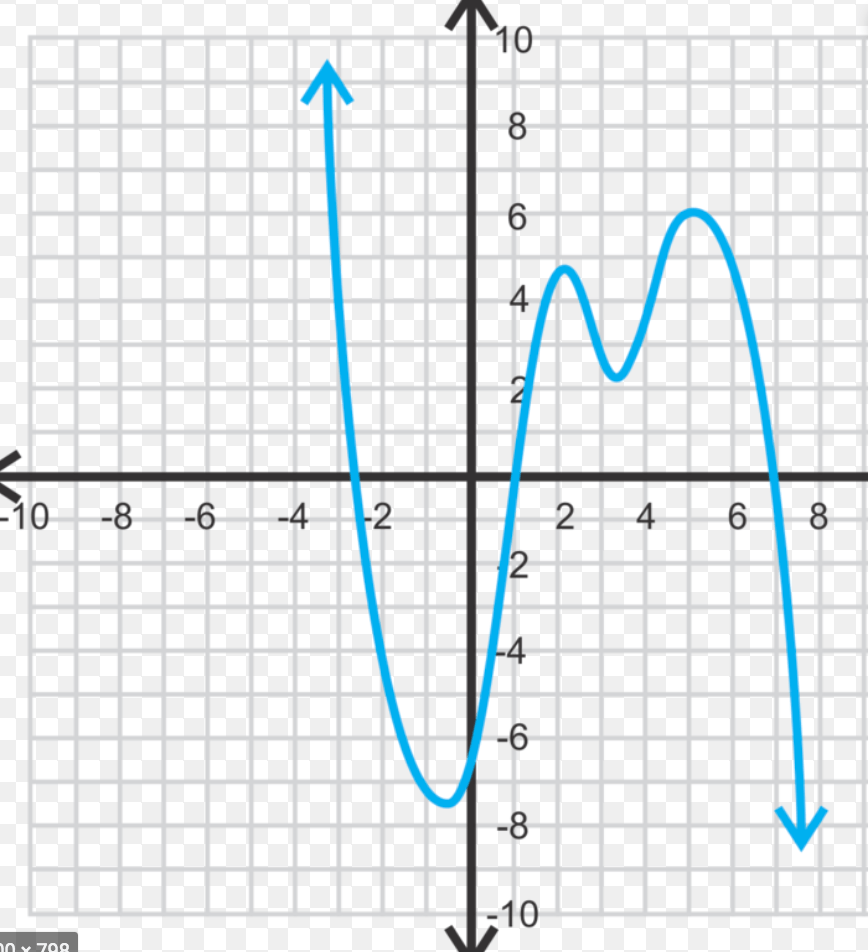
What is a) -3
b) approximately (-2.5,0) (1,0) (7,0)
c) (0,-6)
300
Which of the following is a solution to the inequality |x -4| +3 ≥ 9?
-4, -1, 0, 2, 10 (select all that apply)
What is -4 and 10
300
Evaluate f(x) = 3|x-4| for x=-3, x=0, and x=3
What is 21, 12, and 3?
300
Write the equations for the following absolute value:
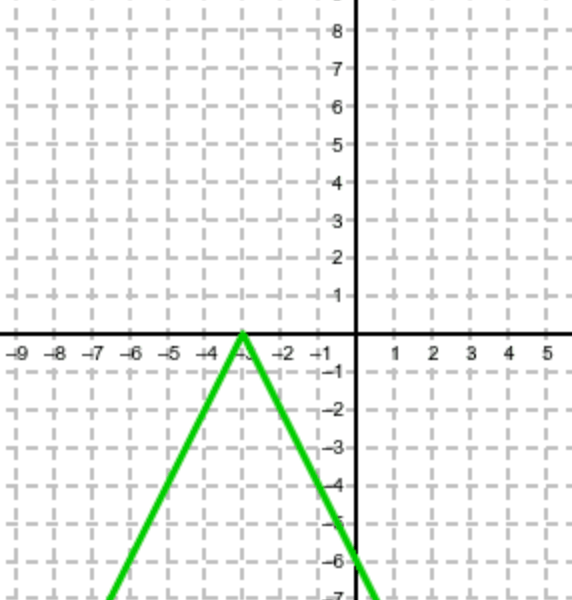
What is y = -2|x+3|
400
Find the domain and range in inequality notation
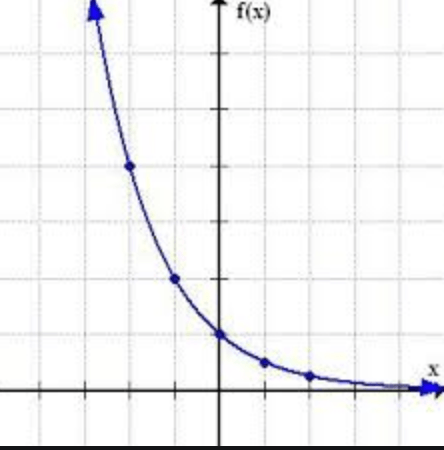
D: All real numbers (-∞<x<∞)
R: y>0
400
Solve
-3|(x-4)| > -9
What is 1 < x < 7? (AND Problem)
400
Solve |x|+4 = 7
What is x=3 and x=-3?
400
Solve:
-1/3abs(2x-4)+3=1
What is x = 5 and x = -1
500
Graph y = 3|x-1| +4
