Domain & Range
Piecewise Functions
Absolute Value Functions
Graphs
Mystery
100
State the domain and range of the following function:
f(x) = x2 - 3
D: All real numbers. (-inf., inf.)
R: {-3, inf.)
100
Given this piecewise function, which equation would I use if I wanted to find f(1)
(top, middle, or bottom)
Bottom
100
True or false: The following equation would move the parent function 4 units left
f(x) = |x-4|
False!!!!!!
100
What makes a graph continuous?
No jumps or discontinuity
100
What is the meaning of a number's absolute value?
The number's distance from 0.
200
What would the graph of y = | x - 3| + 4 look like?
What is a V shaped graph that is moved right 3 and up 4 ;
200
Is this graph a function? Must explain why or why not!!!
NO! Does not pass the vertical line test.
200
What would the output be if we plugged in -1 for x?
2|x-1| + 6
10
300
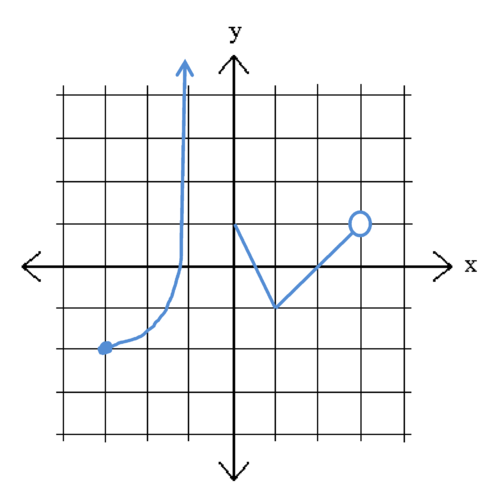
State the domain and range of the following graph: *MUST USE APPROPRIATE SYMBOLS*
D: (-3,1]
R: [-4,0]
300
Given this piecewise function, find f(1) + f(2) - f(4)
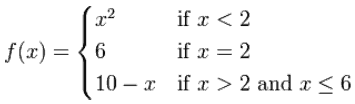
1
300
State all of the transformations that are made to the parent function, |x| to achieve the graph of
-|x+1| - 3
* reflected over x-axis
* moved 1 unit left
* moved 3 units down
300
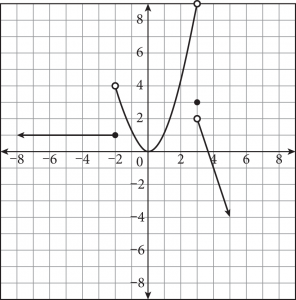
According to the graph above, what is f(3)
3
300
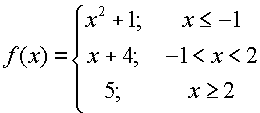
Using the given piecewise function, find 1/2f(-3) + f(0) - f(4)
4
400
State the domain and range for the following piecewise function:
*USE APPROPRIATE SYMBOLS*
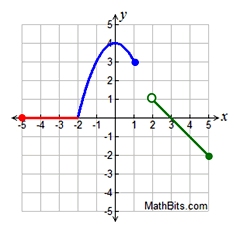
D: [-5,1] and (2,5]
R: [-2,4]
400
Describe the transformation:
The graph of y = -|x + 2| + 5.
A V shaped graphed shifted left 2, up 5, and reflected over the x axis
400
What are x intercepts of this absolute value graph
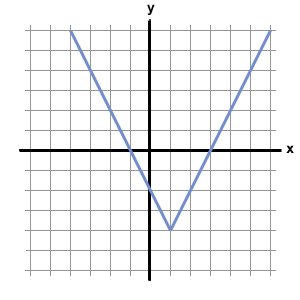
x = -1, x = 3
400
What are the solutions to the following equation?
-4|x+2| - 1 = 1
NO SOLUTION!!!!
500
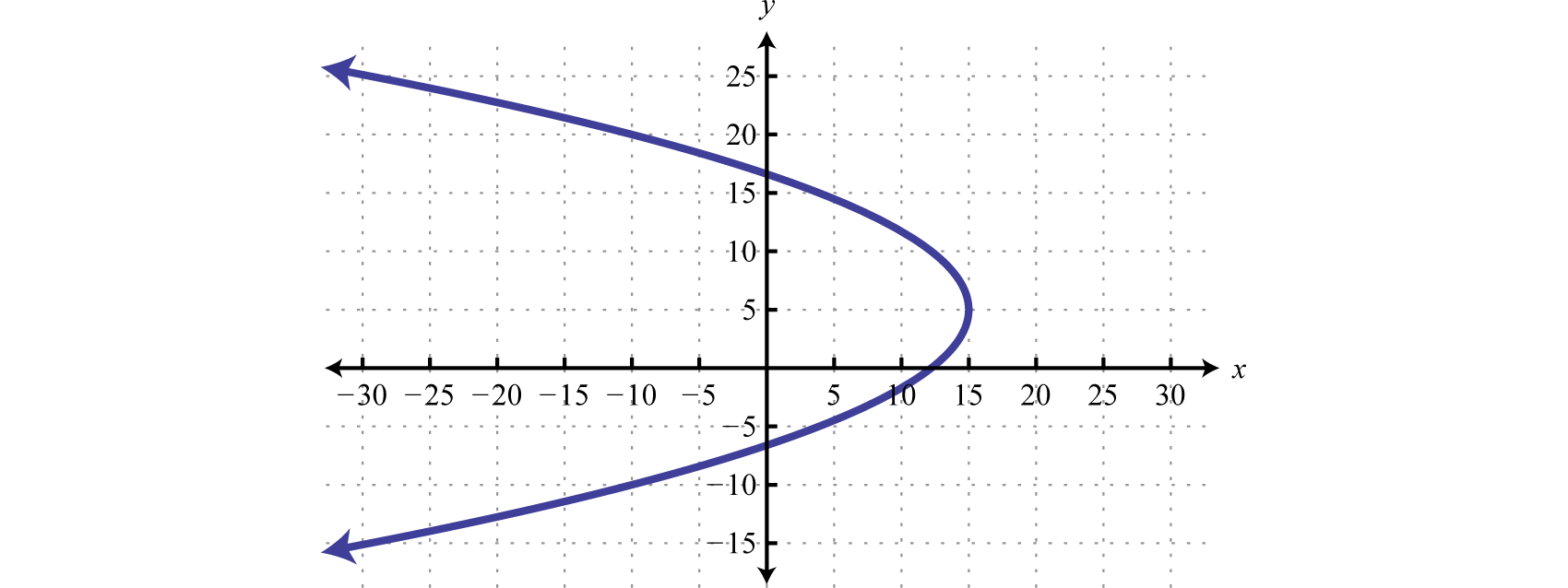
State the domain and range of the following graph:
*MUST USE APPROPRIATE SYMBOLS*
D: [-4,-2) and [0,4)
R: [-2, inf)
500
Write the equation for the piecewise function above. *BE CAREFUL WITH THE INTERVALS*
f(x) { x, -3 <= x <= 0
2, 0 < x < 1
1/3x, 1<= x < 4
500
What are the criteria for a piecewise function?
The function has 2 or more pieces
Each piece has its own domain
500
For the following graph, state the domain, range, vertex, axis of symmetry, intervals of increasing and intervals of decreasing. Must have all parts to get points!
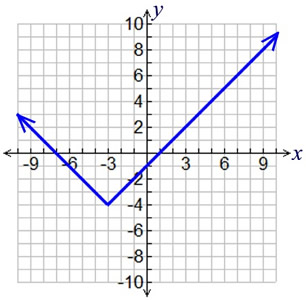
D: (-inf., inf) Inc: [-3, inf.)
R: [-4, inf.). Dec: (-inf., -3]
Vertex: (-3,-4)
AOS: x = -3