All Key Features
Piecewise Functions
Absolute Value Functions
Graphing
Mystery
100
What is the formula for a absolute value function?
y= ± a|x-h|+k
100
Given this piecewise function, which equation would I use if I wanted to find f(1)
(top, middle, or bottom)
Bottom
100
True or false: The following equation would move the parent function 4 units left
f(x) = |x-4|
False!!!!!!
100
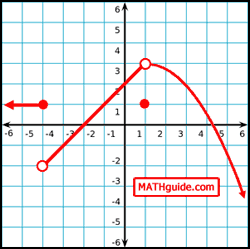
Is this graph continuous?
HECK NAH!!!!
100
What is the meaning of a number's absolute value?
The number's distance from 0.
200
Which direction is this graph going?
y=-2/3|x-3|+4
down
200
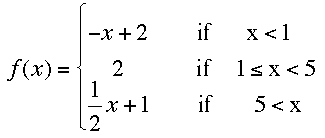
Use the above piecewise function to find f(6)
4
200
Solve the following absolute value equation:
2|x-3| = 6
x = 0 and x = 6
200
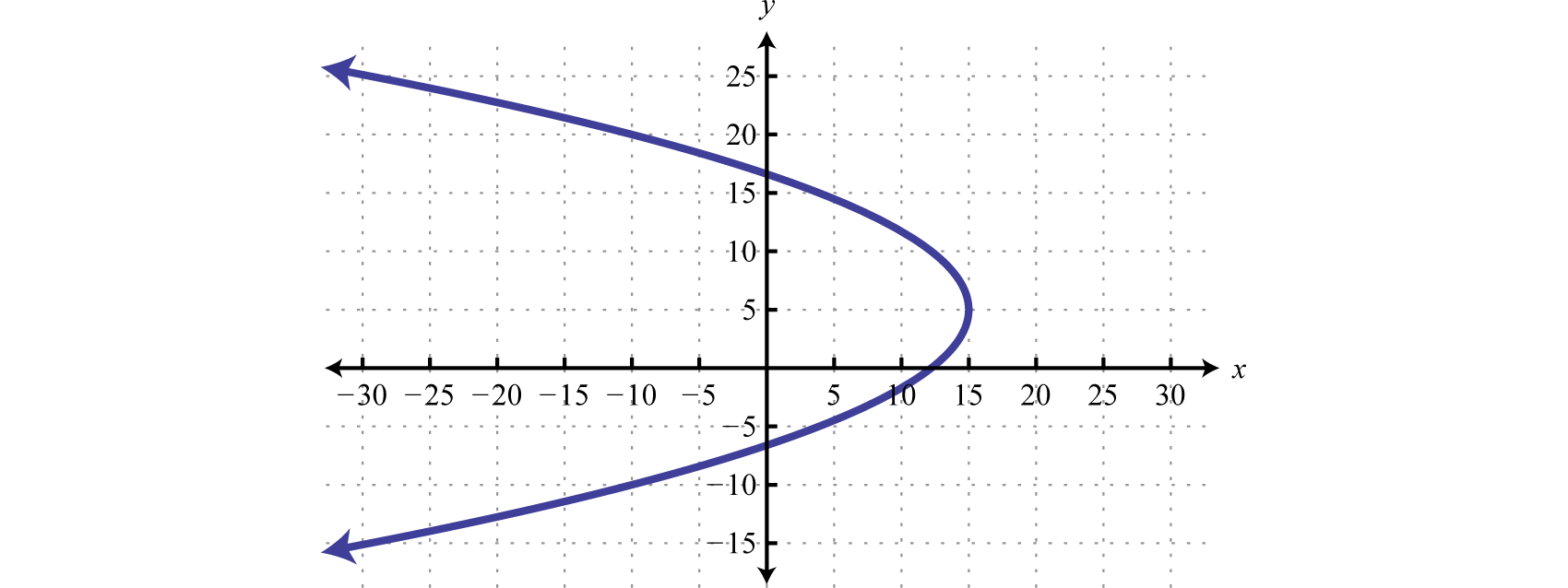
Is this graph a function? Must explain why or why not!!!
NO! Does not pass the vertical line test.
200
What would the output be if we plugged in -1 for x?
2|x-1| + 6
10
300
What is the vertex of this equation?
y=3|x+5|-8
(-5,-8)
300
Given this piecewise function, find f(1) + f(2) - f(4)
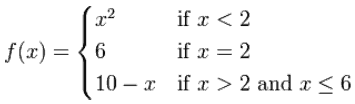
1
300
State all of the transformations that are made to the parent function, |x| to achieve the graph of
-2|x+1| - 3
* stretched twice as far
* reflected over x-axis
* moved 1 unit left
* moved 3 units down
300
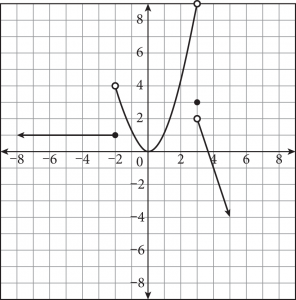
According to the graph above, what is f(3)
3
300
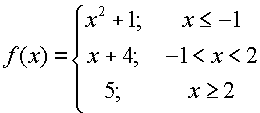
Using the given piecewise function, find 1/2f(-3) + f(0) - f(4)
4
400
Write an absolute value equation that opens down, has a vertex of (6,-7) and a ray with a slope of 10.
y=-10|x-6|-7
400
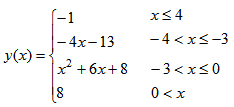
Given the piecewise function above, find f(-1)
3
400
Solve the following inequality and write in interval notation ( #< x < #)
3|x-6| + 4 < 5
5.667 < x < 6.333
400
What are the solutions of this absolute value graph and y = 0?
x = -1, x = 3
400
What are the solutions to the following equation?
-4|x+2| - 1 = 1
NO SOLUTION!!!!
500
Describe the end behavior of this equation.
y=-4|x-3|+2
As x goes to -inf. y goes to -inf.
As x goes to inf. y goes to -inf.
500
Write the equation for the piecewise function above. *BE CAREFUL WITH THE INTERVALS*
f(x) { x, -3 <= x <= 0
2, 0 < x < 1
1/3x, 1<= x < 4
500
Solve the following absolute value inequality, and then represent the solution on a number line.
*NUMBER LINE MUST INCLUDE CUT OFF POINTS*
-3 |x-5| + 15 < -15
x < 5 or x > 15
500
Write the interval for when the following graph is > or = 6.
(-inf., -5] or [1, inf.)
500
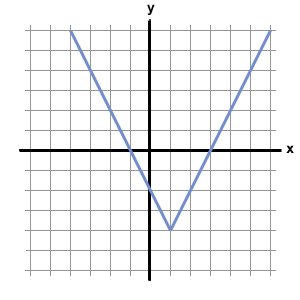
For the following graph, state the domain, range, vertex, axis of symmetry, intervals of increasing and intervals of decreasing. Must have all parts to get points!
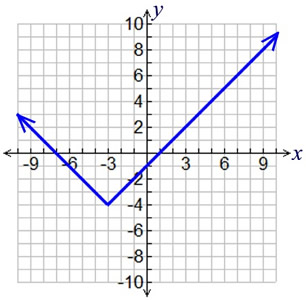
D: (-inf., inf) Inc: [-3, inf.)
R: [-4, inf.). Dec: (-inf., -3]
Vertex: (-3,-4)
AOS: x = -3