Growth/Decay, H. Asymptote and Graphing
Domain, Range, End Behavior
Intercepts
Finding Equations from Two Points
Transformations
100
What is the horizontal asymptote for the equation: f(x)=3*2x-1+2
y=2
100
Find the domain and range
g(x)=1/2*(4/3)x-4
Domain: (-∞,∞) or -∞,<x<∞
Range: (0,∞) or 0<y<∞
100
Find the y-intercept for the function:
f(x)=1/2(2/3)^(x+1)-3
(0,-8/3)
100
Find the exponential function of form y=a*bx that goes through points (0,3/4) and (-1,3/8)
y=3/4 * 2x
100
Describe the transformations compared to the parent function p(x)=2x:
f(x)=1/3*2x-2
Vertical shrink by 1/3
Shift right 2
200
Graph the function f(x)=3*2x-1+2.
Make sure your graph includes everything necessary!
Please ask Matsu to look at your graph!
200
Find the domain and range
h(x)=2/3*(1/3)x-2+13
Domain: (-∞,∞) or -∞,<x<∞
Range: (13,∞) or 13<y<∞
200
Find the y-intercept
h(x)=2/3*(1/3)x-2+13
(0,19)
200
Find the exponential function of form y=a*bx that goes through points (-2,2/9) and (1,6)
y=2*3x
200
Describe the transformations compared to the parent function p(x)=2x:
f(x)=4/3*2x+3-4
Vertical stretch by 4/3
Shift left 3
Shift down 4
300
Graph the function g(x)=1/2*(4/3)x-4
Make sure your graph includes everything necessary!
Please ask Matsu to look at your graph!
300
Describe the end behavior:
h(x)=2/3*(1/3)x-2+13
as x→-∞, y→∞
as x→∞, y→13
300
Find the y-intercept
g(x)=1/2*(4/3)x-4
(0, 81/512)
300
Find the exponential function of form y=a*bx that goes through points (-1, 5/24) and (2,45)
y=5/4 * 6x
300
Write a function with base 4 and the following transformations:
-Shift up 4
-Shift right 3
-Vertical stretch by 5/3
y=5/3 * 4x-3+4
400
Find the exponential equation of the graph given the form below with a vertical stretch of 3/2 and a decay rate of 4/5 in the form y=a*b^x+k
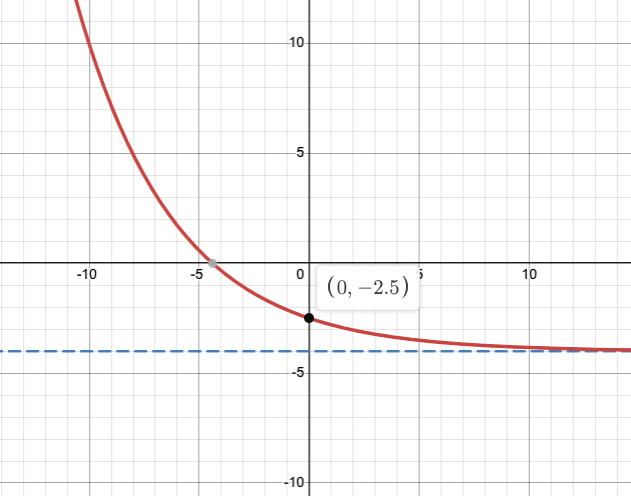
y=3/2(4/5)^x-4
400
Describe the end behavior:
g(x)=1/2*(4/3)x-4
as x→-∞, y→0
as x→∞, y→∞
400
How do you know if the following function has an x-intercept without graphing it?
f(x)=3*(2/3)^(x-4)+3
the k value of 3 means that all y values are above 3, which means the exponential function will never touch the x axis.
400
A very expensive pair of shoes increases in price exponentially. After two years, it costs $46,875 and after 3 years, $58,593.75. Find the original price of the shoes using the function
y=a*b^x
$30,000
400
DAILY DOUBLE (800 POINTS)
find the exponential function with a vertical stretch by 2, base of 1/3, vertical shift up 4, and goes through point (2, 14/3) given the following characteristics in the format
y=a*b^(x-h)+k
y=2(1/3)^(x-1)+4