Functions
Domain and Range
Rate of change
Behaviors of Graphs
Composition of Functions
100
What is the definition of a function?
A function is a rule between two sets of objects in which each object from first set is assigned to exactly one object in the second set.
100
Define Domain
set of all possible input values for a function i.e. x-values
100
Define rate of change
An average rate of change describes how one quantity changes with respect to another quantity over an interval
100
A function is increasing on an interval [a b] if...
f(a)<f(b) for a<b
100
Find f+g(x)
f(x) = 2x-1
g(x) = 3x
5x-1
200
Is it a function?
x y
1 5
3 6
2 10
Yes
200
Define Range
set of all possible outcomes for a function i.e. y-values
200
Formula for rate of change
change in output/change in input
200
A function f(x) is decreasing on an interval [a b] if...
f(a)>f(b) when a<b
200
For two functions to be the inverse, f(g(x)) ____ g(f(x))
AND
both must equal ____
=
x
300
How to test if a function is 1-1?
Horizontal line test
300
Write -2<x<=2 in interval notation
(-2,2]
300
Find average rate of change f(t) = t^2 over an interval [1 2]
3
300
Local maximum occurs when a function changes from ____ to ____
increasing
decreasing
300
f(x) = 2x-1
g(x) = 3-x
Find g(f(x))
4-2x
400
Evaluate
f(x) = x^2 - (1/3x)
for f(-1)
4/3
400
Find the domain of
f(x) = ((x+10)^1/2)/(x)^1/2
[-10,0) U (0,inf)
400
Find average rate of change f(x) = x^2 +2x -8 for [5 a]
a+7
400
Local minimum occurs when f(x) changes from ____ to _____
decreasing
increasing
400
Rewrite the function as g(x) and h(x)
f(x) = 1/(x+4)^9
g(x) = x+4
h(x) = 1/x^9
500
Is y=x^2 a 1-1 function?
No
500
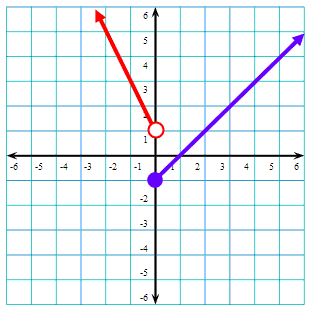
Find the domain and range
Domain: (-inf, inf)
Range: [-1,inf)
500
Find average rate of change for f(x) = 1/(x+5)
for [x, x+h]
-1/(x+h+5)(x+5)
500
Find local extrema
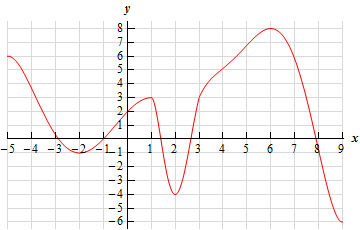
Local max:
8 @ x=6
3 @ x=1
min:
-1 @ x=-2
-4 @ x=2
500
f(x) = x^2 + 2
g(x) = 1/x
h(x) = x-1
Find f(g(h(x)))
(1/(x-1))^2 +2