The South Polar
These equations are Differential
Parametric This
Keep Em Seperated
Potpourri
100
a) Plot the point with polar coordinates (4,2pi/3). Then find its Caresian Coordinates. b) The Cartesian coordinates of a point are -3,3. Find two sets of polar coordinates for the point.
What is
a)
(-2,2sqrt(3))
b)
(3sqrt(2), (3pi)/4)
(-3sqrt(2), (7pi)/4)
100
The equilibrium solutions to y'(t) = y(y - 3)(y + 2)
What is y = -2, y = 0, y = 3
100
Consider the parametric equations:
x = t - 1, y = t^3
a) Eliminate the parameter to obtain an equation in terms of x and y.
b) Sketch a graph of the curve.
What is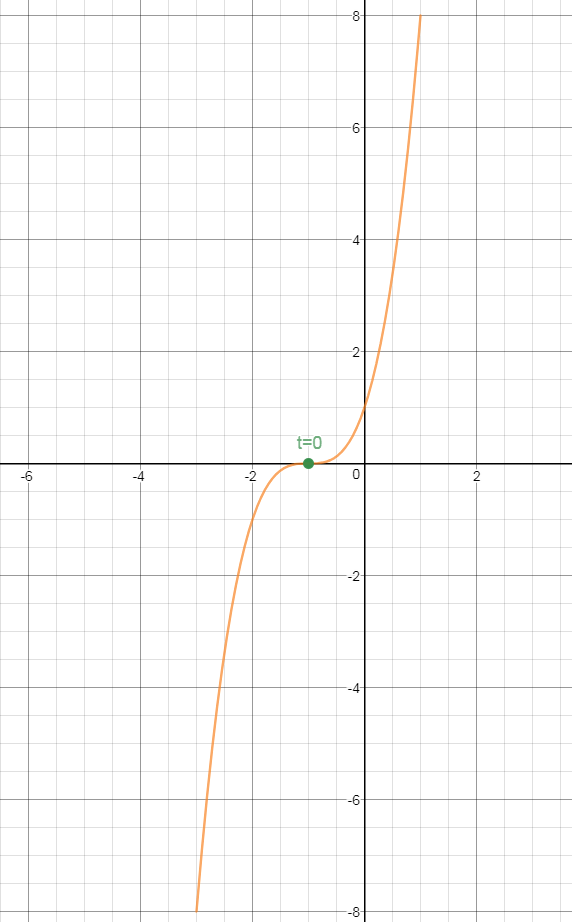 
y = (x + 1)^3
100
The solution to the differential equation
dy/dx = y^2 e^-x
What is
y(x) = 1/(e^-x - C)
100
The arc length of
y = ln(secx)
for
[0,pi/4]
What is
ln(sqrt(2) + 1)
200
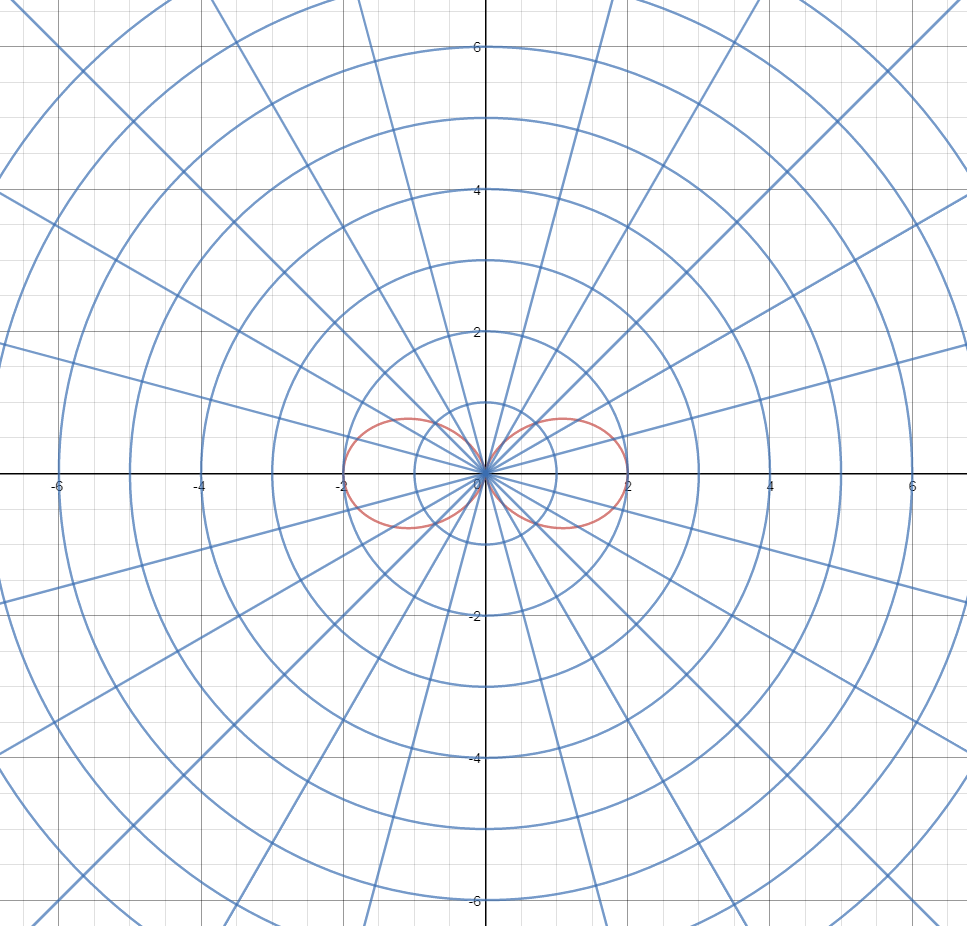
Sketch the polar curve
r = 1 + cos(2theta)
. You must label all three x-intercepts in polar coordinates.
200
Sociologists model the spread of rumors using logistic equations. The key assumption is that at any given time a fraction y of the population (0<=y<=1), knows the rumor, while the remaining fraction 1 - y does not. Furthermore, the rumor spreads by interactions between those who know the rumor and those who do not. The rate of change of those who know the rumor is proportional to product of those who know the rumor with those who do not. Set up a differential equation that models this problem.
What is
dy/dt = ky(1 - y)
200
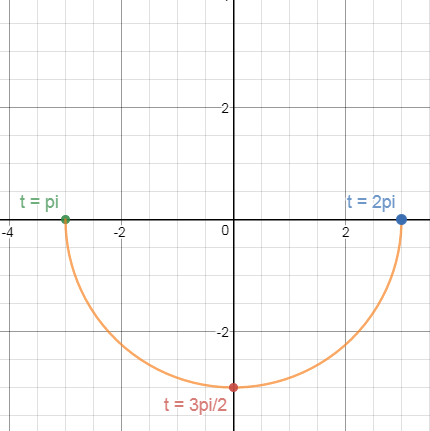
Consider the parametric equations:
x = 3cos(t), y = 3sin(t)
,
pi <= t <= 2pi
a) Eliminate the parameter to find an equation in terms of x and y.
b) Sketch a graph of the curve and indicate the direction of movement.
What is
x^2 + y^2 = 9,-3<=y<=0
200
The solution to the differential equation
dy/dt = (3t^2)/y
What is
y = +- sqrt(2t^3 + C)
200
Set up an integral to find the surface area formed by rotating f(x) = sin(x), on the interval [0,pi] about the x-axis.
What is
2pi int_0^pi sin(x)sqrt(1 + cos^2(x))dx
300
Find the polar equation for the curve represented by x + y = 2.
What is
r = 2/(cos(theta) + sin(theta))
300
The general solution to the logistic equation
(dP)/dt = 0.1 P(1 - P/300)
is
ln|P/(300 - P)| = 0.1t + C.
If P(0) = 50. What is C?
What is
C = ln(1/5)~~-1.61
300
Consider the parametric equations: .
x = cos(t), y = 8sin(t)
Find the equation of the tangent line to the curve at
t = pi/2
What is y = 8
300
The solution to the differential equation:
y' = e^(y/2) sin(t)
What is
y = -2 ln(1/2 cos(t) + C)
300
Find the center of mass for the region enclosed by
y = 4 - x^2
and the x-axis.
What is
(0,8/5)
400
the area enclosed by the curve
r^2 = 9cos(5theta)
What is 18
400
An endowment is an investment account in which the balance ideally remains constant and withdrawals are made on the interest earned by the account. Such an account may be modeled by the initial value problem
(dB)/dt = aB - m
for
t >= 0
The constant a reflects the annual interest rate and m is the annual rate of withdrawal. Solve the initial value problem with a = 0.05, m = $1000/year, and B(0) = $15,000.
What is
B = 20,000 - 5,000e^(0.05t)
400
The equation of the tangent line to the curve:
x = 1 + lnt, y = t^2 +2
at the point (1,3)
What is y = 2x + 1
400
The solution to the initial value problem:
y'(t) = e^t/(2y)
y(ln2) = 1
What is
y = sqrt(e^t - 1)
500
Find the area of the region that lies inside both of the circles
r = 2 sin(theta)
and
r = sin(theta) + cos(theta)
What is
1/2 (pi - 1)
500
At what point on the curve defined by the parametric equations
x = 3t^2 + 1, y = t^3 - 1
does the tangent line have slope 1/2
What is (4,0)
500
The solution to the initial problem
dy/dx = e^(x-y)
y(0)=ln3
What is
y = ln(e^x + 2)