Proportional Relationships
Slope
Writing Linear Equations
Transformations/
Pythagorean Theorem
Pythagorean Theorem
Volume & Surface Area
100
A proportional relationship must go through what specific point on a coordinate plane?
The origin (0,0)
100
To find slope on a graph we count what?
rise over run
100
A certain cab company charges a $1.75 pick-up fee and $1.50 per mile traveled. Write an equation that models how much Jenny's fee would be if she traveled x miles.
y = 1.50x + 1.75
100
True or False: Dilations preserve congruence.
False
100
Find the volume of the cylinder below. Round your answer to the nearest tenth if necessary.
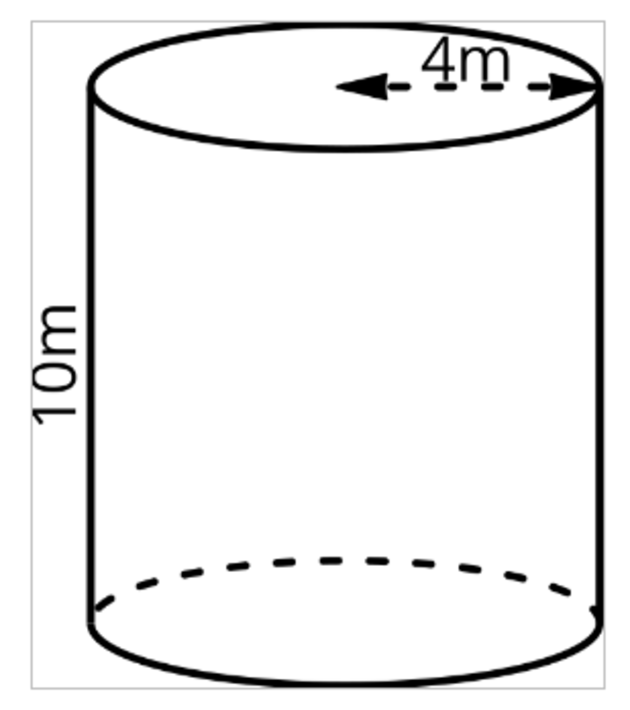
V= 502.7 m3
200
True or False: Proportional relationships have a constant rate of change.
True
200
What is the slope in the following equation?
y = -2x -5
m = -2
200
In order to join a movie rental service, there is an initial $60 fee, then a $5 fee every month. Write an equation in slope-intercept form modeling this situation.
y = 5x + 60
200
What transformation is pictured below?
Reflection over the y-axis
200
Find the volume of the following three-dimensional figure. Round your answer to the nearest tenth if necessary.
V= 150.8 ft3
300
What is the constant of proportionality for the table below?
k = 3/4 or $0.75
300
What is the slope of the graph below?
m = 1/2
300
The cost of a medium cheese pizza is $7.50 and each additional topping cost $0.65. Write an equation to model how much a pizza with x number of toppings would cost.
y = 0.65x + 7.50
300
How far up the wall does the ladder reach? Round your answer to the nearest tenth.
x = 10.2 m
300
What is the total surface area of the following three-dimensional figure? Round your answer to the nearest tenth if necessary.
Surface Area = 684 in2
400
What is the constant of proportionality for the graph below?
k = 6
400
Find the slope given the following two points.
(0,-2) and (3,4)
m = 2
400
Charlie wants to sign up to become a member at Planet Fitness to take some yoga classes. There is a one-time membership fee of $75. Each yoga class costs $15. Write a linear equation to determine how much Charlie would pay the first month at the gym after taking, x number of yoga classes.
y = 5x + 75
400
Write the algebraic rule for the transformation pictured below.
(x,y) -> (x-1, y+4)
400
Find the lateral surface area of the following three-dimensional figure. Round to the nearest tenth if necessary.
Lateral Surface Area = 504 mm2
500
C. 7 hours to build 8 birdhouses
500
Find the slope of the following equation.
2x + 3y = 18
m = -2/3
500
Lucy pays $224 in advance on her account at the health club. Each time she visits the club, $7 is deducted from her account. Write an equation that represents the value remaining in the account after x visits.
y = -7x +224 or y = 224 -7x
500
Round your answer to the nearest whole number.
The TV is 32 inches.
500
Find the total surface area of the following three-dimensional figure. Round to the nearest tenth if necessary.
Surface Area = 571.8 m2