Numbers and Operations
Operations and Algebraic Thinking
Measurement, Geometry, and Data
Instruction in Math
Problem Solving
100
5 x (10 + 4 - 2) + 20 ÷ 5 =
A. 60
B. 64
C. 62
D. 68
B. 64
100
Use the diagram below to answer the question that follows.
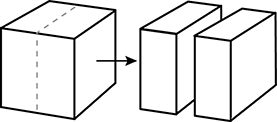
An artist creates a cube using a piece of clay. The artist then cuts the cube in half to make two congruent rectangular solids, as shown in the diagram. Which is the ratio of the surface area of the original cube to the total surface area of the resulting rectangular solids?
A. 1:2
B. 2:3
C. 3:4
D. 5:6
C. 3:4
100
Which of the following correctly describes a triangle with one 90-degree angle?
A. Acute Triangle
B. Right Triangle
C. Obtuse Triangle
D. Equilateral Triangle
B. Right Triangle
100
Use the diagram below to answer the question that follows.
A teacher places a set of blocks on a table and asks a child how many blocks there are. The child points to each block while saying the numbers in the proper sequence from one through five. When asked again how many blocks there are, the child responds by counting the number of blocks again. Given this evidence, which question could the teacher ask to help the child connect counting to cardinality?
A. How many cones, boxes, and balls are there?
B. How is the last number name you said related to the number of blocks?
C. How many different types of shapes are there?
D. How is the first block counted similar to the last block counted?
B. How is the last number name you said related to the number of blocks?
100
A bottle holds 2 liters of water. If you pour 1 liter into a cup, how much water is left in the bottle?
A. 1 liter
B. 2 liters
C. 3 liters
D. 0 liters
A. 1 liter
200
Use the student work below to answer the question that follows.
Step 1: 4.8 • 0.5 =
Step 2: (4 + 0.8) • 0.5 =
Step 3: 4 • 0.5 + 0.8 • 0.5 =
Step 4: 2 + 0.4 = 2.4
Step 3 of this work indicates an understanding of which concept?
A. associative property
B. commutative property
C. distributive property
D. multiplicative inverse property
C. distributive property
200
The expression 16 − 4 ÷ 1/4 +1 simplifies to which integer?
A. 49
B. 16
C. 4
D. 1
D. 1
200
Which shape has exactly 4 lines of symmetry?
A. 
B.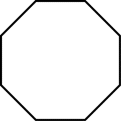 
C. 
D.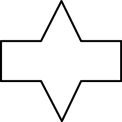 
C.
200
Students are given the information that it takes 3 hours to travel 180 miles. They must determine how far they will travel in five hours. Which of the following identifies how the teacher will best guide the students?
A. Providing them with a chart showing miles per hour.
B. Having them construct proportions.
C. Allowing students to use an abacus.
D. Tasking students with determining the speed of the initial trip.
B. Having them construct proportions.
200
A bus trip takes 3 hours and 45 minutes. If the bus has been traveling for 1 hour and 30 minutes, how much longer will it take to reach the destination?
A. 2 hours and 15 minutes
B. 3 hours
C. 1 hour and 15 minutes
D. 2 hours and 45 minutes
D. 2 hours and 45 minutes
300
Which expression is equivalent to 1 3/4 × 3 5/6?
A. (1 × 3) + (3/4 x 5/6)
B. (1 + 3) x (3/4 + 5/6)
C. 3 × (1 + 3/4) + 1 × (3 + 5/6)
D. 3 × (1 + 3/4) + 5/6 x (1 + 3/4)
D. 3 × (1 + 3/4) + 5/6 x (1 + 3/4)
300
Which word problem could be solved using the expression 14 × (7 + 6)?
A. A baker makes 7 cakes in the morning and 6 cakes in the afternoon, every day for 14 days. How many cakes are made in all?
B. A carpenter builds 7 chairs and sells 6 every other day for 14 days. How many chairs are sold in all?
C. In one day, a florist sells 7 floral arrangements. On the next, the florist sells 6. If arrangements continued to be sold following this pattern for 14 days, how many arrangements are sold in all?
D. On one day, a barbershop has 14 regular customers. Advertising brings in 7 new customers, and 6 more come from recommendations. How many customers does the barbershop have in all that day?
A. A baker makes 7 cakes in the morning and 6 cakes in the afternoon, every day for 14 days. How many cakes are made in all?
300
Use the histogram below to answer the question that follows.
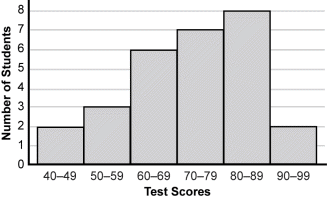
Given the histogram showing the test scores students earned on a recent exam, which statement is a valid conclusion?
A. No student earned a score of 40.
B. The mean score is in the 80s eighties .
C. At least one student earned a score of 100.
D. The median score is in the 70s seventies
D. The median score is in the 70s seventies
300
Use the problem below to answer the question that follows.
A student had 17 marbles, but then lost some of them. Now the student has 5 marbles. How many marbles did the student lose?
Students in a first-grade class independently solve the word problem. The teacher notices some students record 22 marbles as the answer. Which strategy would best help the teacher address these students' misunderstanding?
A. having students use tally marks to count on from the smaller number
B. suggesting that students rewrite the problem by stacking the numbers vertically
C. drawing to model similar problems for the class using a part-part-whole model
D. explicitly instructing students to subtract the smaller number from the larger number
C. drawing to model similar problems for the class using a part-part-whole model
300
A watermelon weighs 5 kilograms. If you cut off 1.5 kilograms and give away 2 kilograms, how much of the watermelon is left?
A. 1.5 kilograms
B. 2.5 kilograms
C. 1 kilogram
D. 3.5 kilograms
A. 1.5 kilograms
400
A bag contains a number of plastic disks that are either red, green, or blue. One-quarter of the disks are red and two-thirds of the disks are green. Which is a possible value for the number of disks in the bag that are either red or green?
A. 18
B. 36
C. 42
D. 88
D. 88
400
What is the slope of the following linear function?
f(x)=3x+2
A. 2
B. f
C. x
D. 3
D. 3
400
Use the diagram below to answer the question that follows.
Given the dimensions shown in the diagram, what is the area of the rectangle?
A. 446.5 ft.2
B. 893 ft.2
C. 1,706 ft.2
D. 1,997.5 ft.2
A. 446.5 ft.2
400
A third-grade teacher is preparing to teach the following standard from the New York State Learning Standards for Mathematics.
Number & Operations—Fractions (NY-3.NF)
Develop understanding of fractions as numbers.
3. Explain equivalence of fractions, and compare fractions by reasoning about their size.
Which strategy is likely to be most effective as part of an introductory lesson designed to meet this standard?
A. teaching that 1/3 is equivalent to 2/6 by showing how they represent the same point on a number line
B. teaching that 1/3 is equivalent to 2/6 because 1/3 × 2/2 = 2/6 according to the rules of fractions
C. teaching that 1/3 is equivalent to 2/6 because 6 is the least common denominator of 2 and 3
D. teaching that 1/3 is equivalent to 2/6 by showing cross multiplication of 1 x 6 = 2 x 3
A. teaching that 1/3 is equivalent to 2/6 by showing how they represent the same point on a number line
400
A shop sells 3 cans of juice for $4 each and 2 sandwiches for $6 each. If you buy all 3 cans and both sandwiches, how much do you spend in total?
A. $12
B. $20
C. $22
D. $30
C. $22
500
Which number represents the greatest quantity?
A. ∛0.216 (the cubed root of 0.216)
C. √0.24 (the squared root of 0.24)
D. 1/30
A. ∛0.216 (the cubed root of 0.216)
500
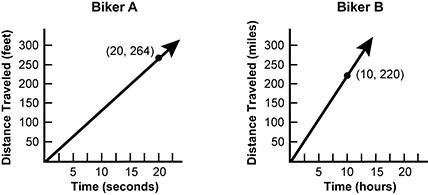
Based on the information shown in the graphs, which value is closest to the difference in miles per hour between the speeds of the two bikers?
A. 8.8 mph miles per hour
B. 10.2 mph miles per hour
C. 13.0 mph miles per hour
D. 19.0 mph
C. 13.0 mph miles per hour
500
Which expression can be used to estimate the number of feet in 2 kilometers?
A.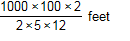 
B.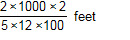 
C.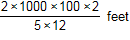 
D.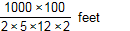 
C.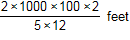
500
Which activity would best help a first-grade student develop a background for understanding congruence?
A. composing and decomposing plane figures into composite figures
B. recognizing figures from different perspectives and orientations
C. determining the measurable attributes of objects
D. modeling two-dimensional shapes by drawing
B. recognizing figures from different perspectives and orientations
500
A runner trains for a marathon by running 4 miles each morning and 6 miles each evening. After 5 days of training, how many miles has the runner completed?
A. 40 miles
B. 50 miles
C. 60 miles
D. 70 miles
B. 50 miles