AMC
AMC
100
What is the value of 9901*101 - 99*10101?
A.2 B.20 C.200 D.202 E.2020
A.2
100
Makarla attended two meetings during her 9 hour work day. The first meeting took 45 minutes and the second meeting took twice as long. What percent of her work day was spent attending meetings?
A. 15 B. 20 C. 25 D. 30 E. 35
C. 25
200
The number 2024 is written as the sum of not necessarily distinct two-digit numbers. What is the least number of two-digit numbers needed to write this sum?
A. 20 B. 21 C. 22 D. 23 E. 24
B. 21
200
A ticket to a school play cost x dollars, where x is a whole number. A group of 9th graders buys tickets costing a total of $48, and a group of 10th graders buys tickets costing a total of $64. How many values for x are possible?
A. 1 B. 2 C. 3 D. 4 E. 5
E. 5
300
The product of three integers is 60. What is the least possible positive sum of the three integers?
A. 2 B. 3 C. 5 D. 6 E. 13
B. 3
300
Shelby drives her scooter at a speed of 30 miles per hour if it is not raining, and 20 miles per hour if it is raining. Today she drove in the sun in the morning and in the rain in the evening, for a total of 16 miles in 40 minutes. How many minutes did she drive in the rain?
A. 18 B. 21 C. 24 D. 27 E. 30
C. 24
400
Zelda played the Adventures of Math game on August 1 and scored 1700 points. She continued to play daily over the next 5 days. The bar chart below shows the daily change in her score compared to the day before. (For example, Zelda's score on August 2 was 1700+80=1780 points.) What was Zelda's average score in points over the 6 days?
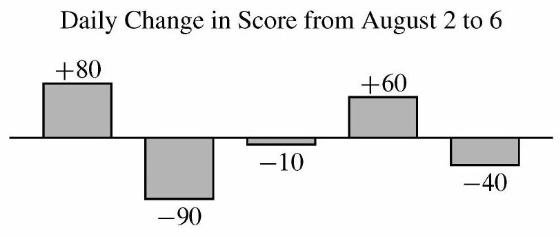
A. 1700 B. 1702 C. 1703 D. 1713 E. 1715
E. 1715
400
The average of the numbers 1,2,3,...,98,99, and x is 100x. What is x?
A. 49/101 B. 50/101 C. 1/2 D. 51/101 E. 50/99
B. 50/101
500
Let 
be the sum of the first n terms of an arithmetic sequence that has a common difference of 2. The quotient 
does not depend on n. What is 
?
D. 400
500
Let a, b, c, d and e be positive integers with a+b+c+d+e=2010 and let M be the largest of the sum a+b, b+c, c+d and d+e. What is the smallest possible value of M?
A. 670 B. 671 C. 802 D. 803 E. 804
B. 671