With 1 litre of cream, Sara can make 400 g of butter. How many litres of cream is needed to make 3200 g of butter?
Sara needs 8 liters of cream to make 3200 g of butter.
Yvan has 15 blocks which he stacks in a triangular arrangement.
Six of the blocks are labelled with an integer, as shown.
The remaining blocks are to be labelled with an integer so that the
sum of the integers in two adjacent blocks in a row is equal to the
integer in the block above them. For example, 3+(−5) = −2. What
integer label should be given to the block at the top of the stack?
9
Lia had her first swimming lesson on Tuesday, October 8th. She had a swimming lesson every Tuesday after that for a total of six lessons. What was the date of her last swimming lesson?
1. First lesson: October 8th
2. Second lesson: October 15th
3. Third lesson: October 22nd
4. Fourth lesson: October 29th
5. Fifth lesson: November 5th
6. Sixth (last) lesson: November 12th
So, Lia’s last swimming lesson was on Tuesday, November 12th.
The diagram shown has nine different regions. Two regions are
bordering if they share a common edge. Each region is to be coloured
so that no two bordering regions are the same color.
What is the fewest number of colors needed?
3 colors
5. Consider the grid shown. Penny draws a point on the grid
with coordinates (x, y) so that
• x and y are integers,
• x + y is even, and
• x + y is less than 7.
How many possibilities are there for the coordinates (x, y)?
There are 26 possible coordinates for (x, y)
A three-dimensional figure was built using linking cubes. The figure, as well as its top view, are shown.
What is the maximum number of linking cubes in the three-dimensional figure?
11 Linking Cubes
Omar went to five different places yesterday. He went to the store after he went to both the pool and the forest. He went to the pool before he went to the forest. He went to the store after he went to the movies, but before he went to the library. He went to the movies after he went to the forest. Which place did he go to second?
The order of places Omar visited is:
Therefore, the second place he went to was the Forest.
Using the diagram below, Ming can draw connected paths from A to B by highlighting line segments. If Ming does not highlight the same line segment more than once, what is the length of the longest path that they can draw?
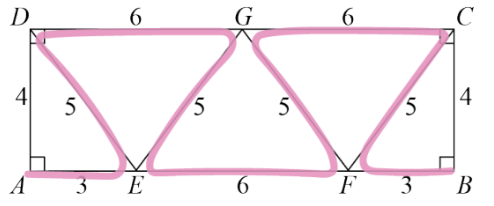
Answer: 44
Aishah wrote a program using block coding to print a sequence of numbers. When her program is run, the first and second numbers printed are 16 and 36, respectively. What is the 2023rd number printed?
Since each number in the sequence is determined by the previous number, we can use the second number, 36, to determine the third number in the sequence. We start at the top of the “repeat forever” block with num equal to 36.We add 2 and so num equals 38. Since num < 20 is false, we move on to the else statement and subtract 10. Then num equals 28. We print 28.
Continuing in this way, we determine that the first six numbers in the sequence are: 16, 36, 28, 20, 12, 28, . . .
As soon as we determine that the sixth number is 28, we stop. Since we have repeated an earlier number, then we know that the next number will be 20, and then 12, and then 28 again. The third and the sixth numbers are each 28, and the numbers repeat in such a way that every third number, or more specifically every number whose position in the sequence is a multiple of 3, will be 28. Since 2022 is a multiple of 3, the 2022nd number will be 28.
Then, the 2023rd number will be 20.
Answer: 20
A game has red and blue tokens. All red tokens are worth the same number of points, and all blue tokens are worth the same number of points. Antwan knows the following:
• Six red tokens and five blue tokens are worth 54 points.
• Two red tokens and three blue tokens are worth 26 points.
If Antwan has one red and one blue token, how many points does he have?
If Antwan has one red and one blue token, he has 10 points.
Jude has six containers. Their capacities in millilitres are shown, where N is an integer.
Jude conducts a series of tests to try and determine the value of N. For each test she chooses two containers, fills them each to the top with water, pours them both into the container with capacity N, and records whether or not it overflows. She then pours out the water and does another test using a different pair of containers until she has tested all 10 possible pairs. Only 4 of her tests resulted in the container overflowing. How many possible values of N are there?
There are 10 possible pairs of test containers. The 4 pairs of test containers that overflowed the container with capacity N will be the 4 pairs with the largest total volume. These 4 pairs of test containers, along with their total volumes, are given in the following table.
Test Containers
Total Volume (mL)
345 and 310
655
345 and 284
629
345 and 275
620
310 and 284
594
From the table, the smallest total volume that overflowed the container with capacity N is 594 mL. Thus, the container with capacity N cannot hold 594 mL and so N < 594.
The remaining 6 possible pairs of containers did not overflow the container with capacity N. The largest total volume of these remaining 6 pairs of containers is 585 mL. Thus, the container with capacity N can hold 585 mL (with possibly more capacity remaining). This tells us that N ≥ 585.
The possible values of N are as follows:
585, 586, 587, 588, 589, 590, 591, 592, 593
Therefore, there are 9 possible values of N.
The mass of 1 m2 of a piece of paper measures its quality and is called its weight. For example, one piece of “300 weight” paper measuring 1 m by 1 m has a mass of 300 grams. What would be the mass, in grams, of a piece of “620 weight” paper measuring 25 cm by 30 cm?
The mass of the piece of “620 weight” paper measuring 25 cm by 30 cm is 46.5 grams.
A box contains some number of red marbles, some number of purple marbles, and exactly 75 yellow marbles. If the probability of selecting a red marble is 35% and the probability of selecting a purple marble is 50%, then how many purple marbles are there in the box?
There are 250 purple marbles in the box.
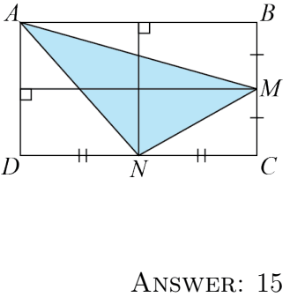
In the diagram shown,
• ABCD is a rectangle,
• M is on BC such that BM = MC, and
• N is on CD such that CN = ND.
If the area of rectangle ABCD is 40 m2, what is the
area, in m2, of 4AMN?
Frankie likes to think about interesting numbers. She learns that there is exactly one four-digit number whose digits reverse when it is multiplied by four. That is, if A, B, C, and D are the digits in the number then ABCD × 4 = DCBA. What is the four-digit number ABCD?
The four-digit number ABCD is 2178