Multiple Choice
Fill in the Blanks
Diagrams
Problem-Solving
100
Which of the following is the definition of area?
a) The distance around the outside of a two-dimensional shape.
b) The distance around the inside of a two-dimensional shape.
c) The amount of space inside a two-dimensional shape.
d) The amount of space outside a two-dimensional shape.
c) The amount of space inside a two-dimensional shape.
100
___________: The distance around the outside of a Two-dimensional shape.
Perimeter
100
What is the formula for calculating the perimeter of the shape below?
Perimeter = side length + side length + side length + side length
or
Perimeter = s + s + s + s
or
P = 4s
100
After completing a word problem involving area, what needs to be included to fully answer the question?
a) The value of the area.
b) The units (i.e. centimetres, metres etc.) squared.
c) A sentence that answers the word problem.
d) All of the above.
d) All of the above.
200
Which of the following is a property of a rectangle?
a) Opposite sides are equal.
b) All angles are equal.
c) All sides are different lengths.
d) All sides are equal.
a) Opposite sides are equal.
200
____________: The value of pi (rounded to two decimal places).
3.14
200
What is the area of this shape?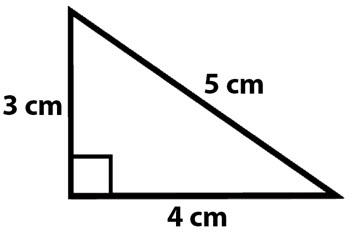
Area = (base x height) / 2
or
A = (b x h) / 2
A = (3 cm x 4 cm) / 2
A = 12 cm 2 / 2
A = 6 cm 2
200
Below is the calculation of the circumference of a circle with a diameter of 2 cm. Identify an error with the calculation.
Circumference = 2 x pi x radius
C = 2 x pi x r
C = 2 x 3.14 x 2 cm
C = 12.56 cm
1) The diameter is used to calculate circumference instead of the radius.
300
What is the relationship between the circumference and diameter of a circle?
a) The circumference of a circle is twice the length of the diameter.
b) The circumference of a circle is approximately three the times the length of the diameter.
c) The diameter of a circle is half the length of the circumference.
d) The diameter is a circle is twice the length of the circumference.
b) The circumference of a circle is approximately three the times the length of the diameter.
300
__________: The part of the compass that stays still and acts as the centre point of the circle.
The fixed arm
300
Identify the name of the measurement depicted in the image.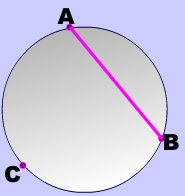
The chord
300
Below is a calculation of the area of a circle with a diameter of 2 cm. Identify two errors with the calculation.
radius = diameter / 2
or
r = d / 2
r = 2 cm / 2
r = 1 cm
Area = pi x radius x radius
A = pi x r x r
A = 3.1 x 1 cm x 1 cm
A = 3.10 cm
1) The value of pi is 3.1 instead of 3.14.
2) The square symbol after the units (centimetres) is missing.
400
What is the definition of an arc?
a) The boundary of a circle.
b) A line segment that runs from one side of a circle, through the centre, to the other side.
c) The section of the circumference that lies between two ends of a chord.
d) A line segment that goes from the centre of a circle to its circumference.
c) The section of the circumference that lies between two ends of a chord.
400
_______: The formula used to calculate the circumference when given the radius.
Circumference = 2 x pi x radius
or
C = 2 x pi x r
400
Calculate the area of the shape below.
Area = Length x Width
or
A = L x W
1) A = L x W
A = 12 cm x 4 cm
A = 48 cm 2
2)
A = L x W
A = 6 cm x 5 cm
A = 30 cm 2
Total Area = Area 1 + Area 2
= 48 cm 2 + 30 cm 2
= 78 cm 2
400
Draw a circle in your notebook. Sketch and label a diameter of 5 cm and a chord of 6 cm.
500
The diameter of a circle is 5 cm, what is the area?
a) 19.63 cm
b) 78.5 cm
c) 78.5 cm 2
d) 19.63 cm 2
d) 19.63 cm 2
500
________: The area of a circle with a radius of 2 cm.
12.56 cm 2
500
Calculate the perimeter of the shape below.
Perimeter = side length + side length …. side length + side length
or
P = s + s … s + s
P = 10 cm + 12 cm + 7 cm + 6 cm + 4 cm + 6 cm + 6 cm + 4 cm
P = 55 cm
500
A washer is an item used in construction to distribute the load when a nut is tightened onto a bolt. The washer has a diameter of 3 cm. The inner circle or ‘hole’ of the washer has a diameter of 1 cm. Calculate the area of the washer itself.
diameter of the washer = 3 cm
diameter of the inner circle or hole of the washer = 1 cm
circumference = ?
Area = pi x radius x radius
or
A = pi x r x r
radius = diameter / 2
or
r = d / 2
1) The entire washer.
r = d / 2
r = 3 cm / 2
r = 1.5 cm
A = pi x r x r
A = (3.14) x 1.5 cm x 1.5 cm
A = 7.065 cm 2
2) The inner circle or ‘hole’ of the washer.
r = d / 2
r = 1 cm / 2
r = 0.5 cm
A = pi x r x r
A = (3.14) x 0.5 cm x 0.5 cm
A = 0.785 cm 2
Area of the washer = Area of the entire washer - area of the inner circle or ‘hole’ of the washer
Area of the washer = 7.065 cm 2 - 0.785 cm 2
=6.32 cm 2
The area of the washer itself is 6.32 cm².