Quadratics
Quadratics
Triangles/Trig
Trig
100
What are three properties of quadratic relations that we learned about in class?
1. Degree of 2
2. 2nd differences are constant
3. Shape is parabolic
100
Based on the quadratic relation:
y=2x2 + 10x - 12
1. State the direction of opening (up or down)
2. State the y-intercept
1. Opens up
2. Y-intercept is -12
100
Similar figures have the same shape but different size.
We can conclude that the triangles are similar if which two conditions are met?
1. Corresponding angles are equal (AA)
2. Ratios of the corresponding sides are equal (SSS)
100
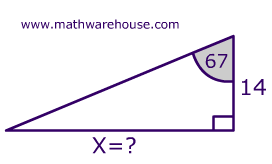
Find the value of x to the nearest metre.
33 m
200
Draw a parabola and label the following:
X-intercepts (zeros), Y-intercept, Vertex, and Axis of Symmetry
200
Expand and Simplify.
(x - 4)(3x - 1)
=3x2 - 13x + 4
200
Draw a detailed, labelled diagram of two similar triangles
Answers may vary
200
Draw triangle ABC where angle C is 90 degrees, b=6 cm and c=10 cm. Find angle A to the nearest degree.
53 degrees.
300
Based on the quadratic relation y =2(x-3)(x+1)
State the y-intercept, the zeros, the axis of symmetry, and the vertex
y-intercept is -6
zeros are 3 and -1
A.O.S is x = 1
Vertex is (1, -8)
300
Factor each of the following:
1. x2 + 12x + 20
2. -15x2 - 48x - 9
1. =(x+10)(x+2)
2. = -3(x+3)(5x+1)
300
Determine angle C based on the information about triangle ABC.
Angle A = 56 degrees
a = 98 cm
c = 112 cm
71 degrees
300
An airplane approaches a runway at an angle of descent (depression of 30 degrees. What is the altitude (height) of the airplane when it is 15 km away from the runway? Round your answer to the nearest tenth.
Altitude is 8.7 km.
400
Determine the equation of the parabola based on the following information:
-Zeros are -1 and 5
-Parabola passes through the point (0, -10)
y=2(x+1)(x-5)
400
Factor each of the following:
1. d2 -121
2. 9a2 -24a + 16
AND identify the type of special case
1. =(d-11)(d+11)
2. =(3a - 4)2
400
Ms. Sestili is standing beside a lighthouse on a sunny day. Ms. Sestili is 1.6 m tall. Her shadow is 4.8 m. The lighthouse's shadow is 75 m. How tall is the lighthouse?
25 m
400
Determine the measure of angle R to the nearest degree based on the following information about triangle QRS. Round your answer to the nearest degree
r = 3.2 km
q = 6.2 km
s= 5.9 km
31 degrees
500
Express the following in vertex form:
y=3x2 - 12x + 9
You can use any method!!
y=3(x - 2)2 - 3
500
The height, h, in metres, of a toy rocket at any time, t, in seconds, during its flight can be estimated using the formula h= -5t2 + 23t + 10
Determine when the rocket will fall to the ground
At 5 seconds.
500
Before rock climbing, a climber needs to determine the length of rope that is needed. She paces off 150 m from the base of the cliff and sights the top of the cliff with a clinometer and measures it to be 70 degrees. What is the height of the cliff?
412 m
500
Two people looked up in the sky and noticed a drone in the air. Person A saw the drone at an angle of elevation of 65 degrees and person B saw it at an angle of elevation of 80 degrees. The two people are standing 30 feet from each other on the same side of the drone. Calculate the height of the drone.
63 feet