Round to the nearest whole.
234.56
235
The farmer's market sold 307 pumpkins last weekend. On Saturday they sold 179. How many did they sell on Sunday?
307 - 179 = 128 (answer)
Ms. Perry placed a border around the bulletin board. If she wanted to measure the length around the bulletin board, what would she be measuring?
Area
Perimeter
Volume
Perimeter
Phil was considering all the possible outfit choices of pants and shirts he had to wear to school. The list below shows the different choices:
Color of Shirt Color of Pants Type of Shoe
Navy (N) Khaki (K) Boots (B)
Red(R) Grey (G) Sneakers (S)
What are all the possible outfit choices?
Navy - Khaki - Boots Red - Khaki - Boots
Navy - Khaki - Sneakers Red - Khaki - Sneakers
Navy - Grey - Boots Red - Grey - Boots
Navy - Grey - Sneakers Red - Grey - Sneakers
2, 6, 10, 14
what is the rule for the pattern above?
+ 4
add 4
Order these fractions and decimals from least to greatest.
1/8, 3/8, 1/2,
0.125, 0.375, 0.5,
Claire's sells bracelets for $4.99 each. Michelle bought 4 yellow bracelets and 5 pink bracelets. How much did Michelle spend at Claire's?
$4.99 X 9 =$44.91 (answer)
Andrea is buying a rectangular rug that is 3 feet wide by 4 feet long. What is the total area that the rug will cover?
a. 12 square feet
b. 14 square feet
c. 12 feet cubed
d. 12 feet
3 x 4 = 12
a. 12 square feet
<img data-fr-image-pasted="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAuoAAAHuCAYAAADJHiktAAAgAElEQVR4AezdV7CmS1X/8Zd4yBxyzhkOOeekCAhIVMyCqcqyLL2wvPBCvfHGMl9YolIiJoKg5JxzzjnnnHM6//r0f75D87JnZsPM2bNnn+6qZ/rp7tUr/Nbq7vU87zMz5zjzzDPP3KyyEFgILAQWAguBhcBCYCGwEFgI7CsEzrmvtFnKLAQWAguBhcBCYCGwEFgILAQWAgOBlaivQFgILAQWAguBhcBCYCGwEFgI7EMEVqK+D52yVFoILAQWAguBhcBCYCGwEFgIrER9xcBCYCGwEFgILAQWAguBhcBCYB8isBL1feiUpdJCYCGwEFgILAQWAguBhcBCYCXqKwYWAguBhcBCYCGwEFgILAQWAvsQgZWo70OnLJUWAguBhcBCYCGwEFgILAQWAitRXzGwEFgILAQWAguBhcBCYCGwENiHCKxEfR86Zam0EFgILAQWAguBhcBCYCGwEFiJ+oqBhcBCYCGwEFgILAQWAguBhcA+RGAl6vvQKUulhcBCYCGwEFgILAQWAguBhcBK1FcMLAQWAguBhcBCYCGwEFgILAT2IQIrUd+HTlkqLQQWAguBhcBCYCGwEFgILARWor5iYCGwEFgILAQWAguBhcBCYCGwDxE4917o9N3vfneIOfPMMzff+973Nuc4xzlG2/05z3nOcRlzr7hXvvOd74zrAhe4wOgzr7GZx7e//e3Rf+5zn3vjmnlEp2++H0Rbf9ATDT3oVtGn7TrXuc71Q3zohOZY/ON3KtRsza65nu/hxGZ9c3/3Myb6lPrm9rHwiFbdfVjnp9p4pVc2FFfGmp9MbT6tJGNbz8bVaGa52sl0r6RPdfO22/WPSYf+QDPrPuuUnJn+ZNzTyXqh56wT3V3GszVa7RlrekdzMmw40TLz08xXn7Jt90yzl/f04bN8lM7a+fFYPmmOGm282ufxidde2rYtKz31Z1P1jEE26Kt0H308tLf5Nr+5O9VhpXZeOafiBasTUeAfr86ydCNXqX0kedt2Z2t8m6d/u8+YfjIOYtnGho0n0taZP77a4Xy8cvJjfPKTmhz9+bOxaPOr/mh28q9xcaee9zt8XDvZg1Z/fLvXr9Q2Lh9Mz1m3nXRJ1jyGZ/PdJ3Om2a/3J2aHOIp1ARawAcWRNqvA0g+8ANQfDR4uJboOhfihj5exefwo6v3AkPmCYXZoPGfZ6fkDk3dIArfHT6X2jCe92ZwPtI3DuD5+UPJHc8Ky8UF06I8j4bhNQ0Z84qvmK6Xx0Tik60689Sl0SR91/cloLB5znYztOh3irV0f2p14JKc5aJpX36xv49uyT0abfvSZ9XOfzY1HI170ZV/zBoMD8Ee+yf79alI+sHboquhTtOc1PTqP8Ed+neci1e46wtQ96571yFbC6Z7e6uye9Y8uZdGZF24z72iOVBcbjSd71qOx46nbk+Nbm336lGTvJCcaY+7js9McffGN9lj8d5J5qvQVI2olm9UnooQ1XmS4dsL9eGTFL/5kuvfgaN03rm7M+G6LeXK2mc8sa+Yz8+1saNwam/M3urh+lEIH18y7PnzS8UfheTJpz/I36jPAHPDNb35z2LsTUGj1n+c85xk1Wn3nP//5R1Lvfga+IPv6178+eJ7vfOfbnHbaaYedgJc58T0W0OjxnOkLqDZoPNB5yJifGpMz63cseft9nE3st2j4AgYXvOAFh93GKvBooev/xje+MWjhwx/8uV3m+dtjO7XRdxmnj4vcr3zlK5sLXehCm4te9KIjPuLNF4p2sZB/6jP+rW99a2xW7BND9J3H0TS/e7ahd8205iYD7VzwUKJXK/rhTA+Xgg/sosGzWBwEJ/kPemWnezi0uervMha+7Dzvec97GF8mhMlJNue4xeen7GUzDLKX77T3Q4E5PR3Q9HLPf/rbQ4+mJzq28Hd2ubfulWJ33h+Pxu+sHCu+8k+ysh8GfEXnfrlFk6/QsRE+aPFDm23okhHvo9Xxgxeezjbzu442dzdjrUE68wfb7CP0dR1LjvF0VJujdsay37nnmvcmc4oD9welhMNsEzudO3CFjZiBx/EU/L761a8eXjdzTJ1IbNmjqMUJG/jVxZ8XvvCFx341x3520WPGof65nvHaiZZMMaQmw16jmJfM5KD72te+NmTCHM7FIvqd+KdL9sG1uDQ3XNXap1I5vgjbhaVAARbg3/e+921e+9rXbj7zmc8cnjkDjlYieLWrXW048c1vfvNw0C1ucYvNda5znR+YY54Ae/vb37559atfPfjf+MY33tzoRjfanH766cP5Tcj5tY9W50ybaM6k/wc+8IHNJz/5ydF3+ctffnPZy172cODEb7alvlO5Zo9gZ/urXvWqcX+Xu9xlc9WrXvUHDis2orUAP/GJT2ze9KY3bT760Y9urnKVq2z45FKXutTAasZnvt8NRvxSMmFTow9/fPjDHx5xcKtb3Wpzu9vdbnOxi11sxBuexd72wm4h8y+dv/CFL2ye9KQnDT43velNN2ecccZI/NMRvaKeeXlA+NznPjcORLzELvk2leaqm9/9zKONhG2we/3rX7/57Gc/u7nGNa6xueENbzj4mecqHneD117QwJct1jYs4Cg5kJzC4SIXucjof9vb3rZ597vfPZKSm9zkJsM2yc5BKvzDl1/60pc2b33rWzfveMc7Rgzd/OY331z72tc+HAMn22b+Ekdf/vKXN+95z3vG+vn85z+/cV3ucpfb3OlOd9pc6UpXOqqa7FT43/pRPv7xj29e/vKXj9i1f9/61rfeXPKSlxxj++EP/qnAgA3W2Ute8pLNRz7ykc3NbnazcbV28ydadG95y1sG3aUvfenNDW5wg81lLnOZw/s/mpl/cqqNwUqxzj/0oQ+NtU4Ha9wLhqPNj8+xanq0Jq23N77xjWNPE4P2bPvTsUq+pY+Lf9lvX8JTbPAtHKKJJ/lhcSLsie9+qOEKG/u9/ez973//5hKXuMQGtle84hWPS0VnmTNTTDl/rnCFK4w9NKZknyg8+cce/bGPfWzz3ve+d9hh7ctpnKHOHft3MtH/qEXMmIeHS9GW973yla8ce861rnWtgd3FL37xw+zhW0zJ61760peO+LNf/dRP/dTmyle+8q4fish6zWteM9aafcj6tgbo0Z61387Tw0DscHOWJ+o5iRMcDI95zGPGplfgFQgFhg3g7ne/+1gE//qv/zoCyObJsYBF70LvidCi+e///u9xQD7kIQ8ZyaFEPbmznO53wOFw1xxYOrU59g1veMPm+c9//khQBY1ExBMhXdhGt+YeZnYAbiTqFg1fONw9oNiYPIHDs6DPdgn6U57ylLFI7njHO47NB1bGZ/zn+2PBVIygc9DZ1B7xiEdsPvjBD45DxEFnc7n+9a8//JJP0mmW5d54POnvIPqXf/mXsQn/8i//8tgoHWrmRxt9umpLymwGDnGx4ACTiPaWDM0sb3tjmHmzS8Lwv//7v5t3vetdm7vd7W4jcSrZmTexdNhPtY3xhS984TjMPaBJ+Kxbh4Bk6BnPeMZY03A17i3U7Jf9ZMuPqkt+5CMPKxJWfrSXiU2J+n4rHr7p2IsTsXyb29xmc73rXe+YiTpb2Gx9uNiN33/913+Nw/8Od7jD5upXv/q+SNTpuVOx7j/96U9v/ud//mfzile8YvPbv/3bm2te85o/sHbNE6OSM3s/v9pj/HpnTxPLxncTx9F4ueTF0nOe85wRG2LEA23jO+m62z57iHXFZg+K//Zv/7b54he/OM4mD2HemB5NTlihya94eoHwrGc9a/O0pz1trGs42Zc8bKNtHj3dH03Gbm3ZD3ThkF3FjH3uxS9+8VjXkuvjTdSf+9znbp74xCeOB0C48pViXcGTL44X03yEp5db9uMXvOAF4wxllxecYtHe3EuU5mR/ugzljvAHGjLo69LG3+XhRv73ute9bnOve91r4CZRjzYbvfh50YtetPnnf/7nkXOgue51r3v4ASa6I6gwuq3tbLT/ygnZlqyjzd2PY3uSqAPHBiLJcxgIREmfN+ySExsfMNu0PN3ZYLylETQ2Cw534ZXzJWc2jXve857jZxJvJ2yegkIR4GgFzm6DHZ3SQ0G8vDH0hsLDgaC55S1vOXgnR02WsptAGoT7/A/2wAMW/OHAgkc+yM7sRgtryYqFYo6n9zDM3Oh3gxUZJbj408Eh59D0sHCPe9xjJAXegvN9OuOdnPRN/nbtJzY6izdxSV9zXeZ2+LFNoYcxbQkKfWwEYtGYYix8RsehP+KrVqJB76FIYutglDglrznxaU7tk1mz1zqUgHiYdYDd/va3H+uc32AJ00996lMDG+3wnO0/mTacCNn5iH2w8ODCTvfG+LLYOBHyjocHXd75zncOX3lIlZw7xKwhv37R92gxxg482JpdEgwP5nhJ0iWFJ7uwQwn/9vRsszdZZ9YbP+lnj4I2f+mz/1ub6M2LtznxGxOP8oc55kqiJUneXjpPFGO75XMkEemLD772YPuafaVyNDnNTx+0Lvaz2xpW4wcfcqKJ7/HakJ77qWZbBRZ+0bW+rRW5yfEWsSUG5Uftj2GLdxgfD7bFtbPOy01nljfqXoDKm+Rf3liXpKP/cX1q30tvfJwLXgj4pdEvM+JSLLWO0Ig9MSVurQ8vd+QPcDauf9bpWJjzi/n2N+fPnEPSb471Y/HaD+N7kqgDxeVthJ/OLHQ/oz3ucY8bG6CfSn/+53/+8OFu03z6058+NgKg2hw80QPcWzo/YVgkEjNvLx0SHOGnKPQC31OjJziOEvxoyRGQ3oYUhGpzBU0/BUsG6Yif5MsG7a2pfjp42kNvjE0ePASFw0+yR55FZxEYE4CCz6c8FrnDTHIDAweaBUIWOXS2mPz8hXdPnIKlhVrA0tGDDt7km0cW+8z3E62HIPRPeMIThv7GHMol0/SACVv62Rdm3ur6eYwv6OUpl/wWVBvJHPD6yNfXeHrjY9FJbL11pxNs4MRGbx69IbeJkG/D4Fs6scWbanHw+Mc/fsQCe73NgJ9xmIqD/Eouf9ogyGI3v9BL7S2IxISuc3+6q+FpA4UvncKKX/HxEzYZaMSFt25wNU4fD570UdQ2KJiyQ3yKBQ8bYpk+9GA32fCGB95k05++8FLYZLN72cteNmIVvnxofVkf9PBgSQ584Ucf+IpT+PmZVYywQ2zaDM33IEq+jZy+4oxedPQJ2owzu3yCRBYsip2nPvWpo82H+IoLPNnjjaI52nhalx7O2QRz+tCTDXQXJ+R6GEKDF/wrHvgdAObiZQw2anHFHnzEn7encCfXWyRvMx1acOIHD+B84lcburoXY3wDY/zIsJ/Ahq6wkZzSEx75PB95eOFLsvjBek9/OjvA+MSeEn8xRC4ZsIWXODfXmqfLve997yEbDmTiqcbTWyt7kSJu4QdjNGRJFOHGDnsE/cUsHSv8g4df1NR0sx7FDtvEJCzCQ+zwt3UJN/uqPdN6p7+41w8ntohH+zVs8acTDNgtzukmRtFUyLU+FHuytSlO9POpNcJORQzQHV7sDj81nviIJZhpo9EnXmEjnmHAXmvXfbStU3L0GRMv5ogzOvmVjQ3i1l4OO3uE+Len0suvGj59YCf80bCFLtadNejiU+caX8K9NcF3dE4vdfd0Y5+5YkitLYbsEWTAiB5qNhinszMCTbiEF91c/GrNWTd0svdI+IzBjq58KgbsF3jBXdxa284+sSZ27J3wcAbylxh60IMeNLCgk5cyzkVx4VNKfObvm9lBDnnOLbGm4McO9ooxeolF8ujBVjEDd2ufjQqc8LC20eMtVsW3MXijZat1La7hwR7r1nmKxjgZam068A287bfiCk/z9c/j7M0n5sMEVuyBAx58yhbYwkWciUEY0tsash6sR/Lpbs2IQTT4irdiiS7WH7ud03iL8+TyIx72D+dqL1jxRm+fpYs1zha+g51PWPxiDXM2G7PGKmGlHy6PfOQjh+18gl4prqv5vH61c0dMwQUN7FwK7MSL9YTG5QwgT78YcA6y1X7CPrY5C8QaO6xr/WhgCiu66YOXeIAljKx1sQBfhX0VMuk+9zV2tPr7O+DRqI5jjFKAU2wAjBEMAorRCiMZJqAAJ3CNMQq4nsge/ehHD2cA0Bu7+93vfuONhGD1Ewm6X/mVXxnzOOt5z3ve4YRAsJjnk5U/+IM/GAcOnSwihT4OcEkgWdo2DoGCJ0c4zPGlk5++HOS+e/qZn/mZsUEIXBsKuzi25MhnPA5Jm/M//MM/DF70t4nY6GxyFpmD0qGMzkav72d/9mfHWyq80jUs1YKNvj5LsZlrsxWONosHPOABAycy/umf/mksArpY7DYYm6wg/umf/unxoOQNjwXupziXzUJAORgEfYeIAEwP+LVo9MOnAI0GlpIRSaWaDDQ2EjLh4e8hwJSeaMQKu8mn80Mf+tCx4TrY6A5j/vjP//zPsfAsHIuqBUA2fn/91389NggbiMNTsUlImH71V391LLpiVC0W1bBxgLr4ic7Gbnvb2258YiUZwN/CZp+D3GYtDn7iJ35ixA4/KHSxwdkgxCWfsVHM4umg+Lmf+7kRl/zMhzZSG6UNyAFkM6GvuIedjdHDLPvxhgc+Lg+9ZEuWn/zkJx9O0vnPA5ufWfnz937v9wZmdIa7uPfrFHzY1VsXPoWrjfg3f/M3x8/f9NYPK/rRV+w7oB0G8LP5+QWNnewyxn6xJV7p7LvIBz/4wWODMx/e1pdvGcVzSYN19pM/+ZMDI7rAlGw6OPj/8R//cRzEYkm/PjRwe+ADHzjm0skatM7uc5/7jM3W2vi///u/8fBnzTjsxLuXCA4Y+4Y+GIsf65RNDiN7D1utIev8/ve//1gj5NJLPLAXjmjFMxrx4/Cz0ftM7JnPfOZIMPgVL4f9fe973/F3LiQX//7v/z4+sbIOxLE4gr+/L2LfZK+5LjytEb5HRxc84Uy2NWIdikH7LLvgDRN7rr2hQ0Y82AN8WugNl/XKBmvBoYuXvYM91qL905qADz78J/k215rVToa37/ZjsqwFn1WYL/YcdnjD2j7ILna0B5JlTYpt8cIGMUbmr//6r48HGHsoXL3gEcswstf4plgcOUwVsWSsYs3hDUM40UdiBFc2o3fNhW5sYzsbzCcf7uJXDEo8HfzGxCad4SjOFJ/c2VOsUfzYTJ6XQv/xH/8xfMVfCn4+s+NP+JCRHea60tNeQp5P9CQbbOUffhODsPH3c+BInvNXvEu6/Vppnwz/eMMEv7/7u78bfhVb/Nj+55OD9i5rxgOez6Hws97EJrutM/u+dUm2ePiLv/iLQc8uCRFcH/WoR411RBe6SZqtv/wGa+sLVvSyH1sfsORv2DtvjVnrcBDbaKw1nxl2TpNn73GW86d9it3W3Z3vfOdxFpELV2uGLfYt9+zEx1llr+QD2LVPilHrSYzAyMMAOvsn+8lBix89rR36KHwMD+cPLOEq/uUL9gG5ijj1oCIf4k/xIaasWevO/usBvjyFfjDjN36BB3sl8vY1OIoHcluvcKfX3/zN3wxM5UBsNO/3f//3R9KPxlrVT4Z9lS5inmzxSB+8FXiymx/hAn84wkruJd7gjVc+x7tCT3Y418SBMbydyfiyDbbiDPZwE5940oMPxIhYNB9+Yud3fud3xnmItnn2JTmh/YAtzjL7LJudFXiZZ/0odCFbob/72Qb3tQfREf44yxP1bbmzYpTu0s+5XYJGEahAEag2Ks4T8DYZT4LRWHh4CXIbtMPR5gH8aIBm85wLZ3G0b6cEiYVrMQgqi4EjHRieyvHmdBuG4PMWgd7kCV7BIXDpbkMWOJwscZKUsAVPAeNQcfBaOJwt8SLDJiTAHKQ2B/qwXcCxT6EznLQtTsFjodKNjp5K8bT4bUIWqmCni3kWrEOXjfD0kEJvvCQWEn98JL90pLMCP7axGW96pBe+5OurtLDY5uAjxyFs86S7zeDZz372CGCy6CnQ2SLwYeYQl5Dy/Z//+Z8P38CR7haTA4uPbZJ40k1xTzfz6EpvNisw52vjf/zHf3x4IdMfHd42OgekTUysORwlCDZ782zaFqYYsEkr3tBKlL0dYwsduujsgICvzYdf+Ts7zMeXzXwFf/FkvrniQcyx17iEm37WguQU/uyyyeH5h3/4hwNr9+SpYWFT0bZexIF+tTUAc+uDnjYzcSoG6dlmib74Ew/kOgTZLe48WMAKFi4HhT62ucQSGS42ekhA5y8CWzP+7oGHCHFgrgOAXfQTFw4MPoaLQofWVg81fAJ/B4K1ZH1IkhSxYD/ha/FD/xJTurFPMgBXeKGzB6B1kHgggR2e5Ipx8S0ZtVbsDXjSCx3c6A1DSZFvouHlIdqDgAcHsiRP6Ojs8DUXRngZt3bFHxz0k6+Eg3t01tNf/dVfDbkwtC4k+xIK+krQrAN+pbc1n6/EOXvxpL8a1vwGCzh4ABS7EgK+Q8/3cKAzPckRU5Jz61482e/4hY+se35p/XjbZl3YzyVoeJrP9nxNFxc54uzv//7vhy+sCTFBprgxTwKMn2SQPyUadBdvHozQOWytL/yU9i0xb99uX+I36wIfsdP+Ah8XHenVXmivZgM6ccaf4hcd+5wt1qh9hR98q4uPhwh7D6zphKfC13QQf/oldfwmRpwVziZ2kIeP+dmjDRc+YYNYsPadDfjhbVzNh2jYYT/zK5B9x9pwhQ+e4phN3ibS20OlPZ2/vTjgH3uyhFLMSmg8iFlX1gfb4Cle0bKLjR6exBf/iVfriT+tOWtTzBvPXjbTEQ9/P0JcwUQ8wMF5w1brzcsT8sW4mkwxaH+BJ53wZpsHA0k6vCRcfErXzhK0YoFsuohX/MxV+ITuxUYxg95DkQdfOFqfzkMxhyd6hX7WCr+xw5h17yykq1i254t92DrDrSu+hBU6eoUn3cgzTwxai9aCfjrgxXY42p/ELKz5lFy+tofgAUd7Gt3EK8zxtd/Se7bZuLaY53d6ejjBn00u2KjtHR6M7aNyAedrew7c4IC2yxx9dJFcixfnB5nOH7aJHXwV9GiNw41vjbGLr/GFDd/BQmyLH3qLVTQws1eyycOMmIM5nPkRP7ECp/QN+3TQJqt296PjKH/seaK+rQsAldkBDNWvTxAAAmCSJG+XLFqLwoJEy3h0ALRoWkSCUKLqwFfwFMBqc4AMUEEuwNWerByaDhEbmE1KADqkHTj6PO31NshhxamCSnA7ADnLYWDjsrAEO93ItBl6A/Gwhz1syOR8fG0wZAtKGwV92swsZIuIDniwmU0OIBulQ59d5qKhi428N19sFKA2W3Q2VgHnAcMvFQ4NOlpEcMUDX295bbgWIxvxxwNugphteLvYzEfG5uBDjz8sbHbwcZDph7d+ttrQ2ePtHPtsouwmU3LJFkmFt6MWjUTBgn74wx8++PGRGCAbbzopYc5eb3SM/e3f/u1YaCW1sInOfD6xOfGLB5hf+IVfGBsaX1ucNhS6iAExRh9tb2n9JUqblnY64C/m2IjWuAPARgg3sSHexDU6MUxfb5HdSxwcnDBw0NpwJCL8JL7/5E/+ZMQ8X0rSJBlwcvjChe/IxpsMG5kkQpzAH1+xZqOim/5iVhzYaB12/MJ/9HVfTNvYbHBkscebdLFj3fK9DZRsawk+MLVZe9DgZ3i3puHjMHV4SGTo5DAVI+KgT1P4iQ7FGv7874D0Rou9EkCxK4ZsonxP5+KCz7WtSbxgIH7144e3Q80nJujgyg949RcmPaB7aOILtppXoX9vxmHAN/Ty0GUPcCjZJxwcDmbJCj34y2HLZrgqYsma5+/81F5mnM72vcc+9rFjXeL/u7/7u4Ov5MDPyXQVrw5bPvIw6uHAfhZfCZzCdja76KSwR4zzK57wpSufsQEdH4gBa90aLbGwtl0Oa/HGNuuJDdYaH7GPbg499tpr8bR+0gG+/CQ++co6ar+2LuwJ9hW2iS0PgPYI69HbdTHXW0ixXcHXJS6LV5iwly0eOJw/Cmy66OWyTvnPL1IwtIbsp3SyX7Bb4mDvs4bEJT/6hYzO1kb24sef7PbQDxd97IU3vvYB6wZOdCnuzNNWK2KbndYTnTyAe0Ckj9izZtnJb+bATPLnDaW9gQzYZa85sLAmxYM9yssDuopZ+rFffMEDf8mQWLCfivNk2Wv4Tlyw0QMg/3ujaU05I9nJn2hhIV6V/CUO2hvoUJzB2vkBZ4mcvda+Yh+zD9hv6MteZx5avJyz1idezgv+YQO7+RLeLljR5a53vevga23BRQLrYmN+REumh6z2bQ/Mv/ZrvzYw/Mu//MvhU3ZZb2LBW3JnLzvws/d5ueQhypqyj9rf7b3wZYM4cqbZY/waz2a+Kxbc40kPMdQ+Zo9ik3WBN7vkIvY9PpNzefHplzfxa82yTbzaZ+wH8hd7pXUgVir8hE5M2CPhqohl+5UCVz50zsHZ2cE2D3fm8xlc0OFPtrYx55i5fAlzZ7IYskf4y9TyFLahF2NssifoK7Zh4aKfc1fsigP7EtzJ4wNxIMfBBxbWh/2Z/fYhuIjT9nG4z2uRrdrFbuMDhGP8cVIS9ZRXuwDhYoCiFthqTma4BQ3s3vRxhHGA46GYw1kCzROTzcSCd4hwgEAyB0DNFTiSJM7pLVFJoSC08C0cgVawmMMhgsYBYzEJPEHm8KWDjQBfdtno0Rak9KOLTcKhxkabto2keWwSmBaTBMAiteHoRy/ZcaDRQxAZs2AFC2zIpZtAtqHasMlH66CwYVrcfn7UBzuBaiNAK/AEdE+XbA83etmYPFXCkSw2sZE+6BS1xYgnW8mx8cKK39gKWzyMobXJ2CxsnNp0Mu5S0MMAb/aQy75iAJ17+irsUujFx3xlYdEdtsWZOexSkwtz45JaB50FSUeyJCYWOTvClTy+tKnQMazoAx90HuRspuLEYWih48+X+PKbAkcxb1MQQw4b9LAQm/iJVTwdbuKGXTZhhW4wdLDhKy7ojodN2iZvbTisS1yvaMYAACAASURBVCLoWQw6sMSIA8vBwmfiRR9+xQIb6aLtEGC/e/EPA7ElBhX8raHeOlsT4tcGCUd492AmZm2S+LS+8Sav2HGvkC8OtF30gwn59LWB82t+bs7se7hrk4UHnu5d+LCd/mxUW2P8Rg4M6SaWxQ5d1Pi0rsUPHMyx8Us8+AuucIC3eIQ/OnPFAD5ddHJASATV5GS3MRe+EiV6kyUu7DPkO2QkoWIPrnRWs0XMOmjFGnnKLBfmZIlJ+4JkHy940N2ahTUa+JCfXfmfXnwsDvHLPuvS2hKX4tyDMLzFhgOX39DiqcCGbdaROQ5icYOPeTCUkNpvzGM//uxVo7OG6CEu4EZvWNDdWuEX+4q9X2IiRtmafejCyT0einF+ldDTCQ05YWmcTjBnh34xYo8lXx9ebI6/vcg+Lc5gyq7WDHq0anpYe+r0w0OfNSHx4Qt7lwck9/wAF37hT/Gj375kTcBRG398yKeHQi58JOnix54jttFrk2MNmwdnsaU2no4wlujjAxu2Sy69lbc/SYasXxjQn3/hNWOEF73FtcIO5414EZv2SDrQ1xrH10Vf42wMb3z4X5+zwvlvjdPdmjNfbLRu9Nlz7Wn2LA/xMBID9KIn7MKLXvZt860hlz3S2kSH3jzYW1P0JE+bbuKdDvBgF0ysRy/c7NXstO+LMWPOG3SwwJcMtlgDcOQPe7Jcyf4lDvCmF59YY8bdS5rpgI7+dMVDXualhTjCmx8raMQgfdxX6FmffjHhAcNapos5HrTFPdvtweyDE7+Qyx56iOHi1J5BV5iIYXIU6w1PsvATU+LYeWotsVkMwIN8MsSw+JBXKeb1IpYca0r8Wud+pfOwYJ/tF1+yk2l+bfczFmh2U76P6m6oTxBNygmc7gHv0i64BZg2oG2UQMxJ0bbAGY9WsFg87m0cglvy7PJWwWFjYRkXLPjg6wC02GysnGej8VTlCc1iUoAtMFzpS0eOtkAtCs5TOzAkhAKdTnijNTdd6Y5WwLHZpU+bfugVPAUfHBS1Q4dMbz78XIWvxeJw7lARePTEF60aHRlsJ0Mfu7JDbVwfPQowgWzMHP0Wsw1JCUMHKJpkss3GAk+LKdv5kK6SAxixT5+NzrdgFq5NAu5kwQvfZFXHr7a6RUBvemizlS5hyx/sbl5z2Kigm+1Ay254whGdKzuNu0dDbry1Fbz4TELuba8NiY02VRuBTcV8cWguevzNpwv92GqzcMHKeDaak8zmw1sC4HDzhlByYuNXPLTi580aXvyo7kFCcoO/zcimRk8bkbiip34bWbiRSc9w43P80aJxZROdrQkXmWFEL3TkqvGyQasdBGRYu9qzrcOgQ3/gxdcuctDSIV9qo8Efjnzpvo3aHOPmKGr6KK0Fsl1oFeP4Ny/6eKFx34UP29HZm8h2tfE7BKwHMWqNkZU+9G8fTJ7axQ6Y8yVZxXtj6pkXGm398z0+FXZpG4epNUt39+xwmZ/95rlnz9xHDt2tATEuzuhq7Uvwvb3DuwdMb/GsNTHs7xSxJTvIsMd5C2h/ENMOXAmWw17s4V/J53RI79mv6clGtooJspVsDKd04LsZJ7R0ta59bmOv50/xy17y8MBP0Y7X6DiEW/d0RiNJ85bRLwH87tyyZ4oRsUNPerAhGfjGv3u4u/glerXETPJIb0kYvuKueOAjtqYrOcYkTB4YJCl85Syiiz2NDGOSHbqaDws+9MIMJuEHjxLV9JKoW+cSbg9tEls+kTQ7X+wZdJht5nMX3FwSUbzZo0ig2CLx9+IBTeeLuEPLRnLsC2whQ6znM/pX6IreGFzRucyBfeN8rq2gpwOM9KONXn/+Q8v2HlbsBfbjmRdac415kJDb2KetATmPOOmhJtnpoc1OeClhZm24pyfe7tMvf7ELNq0ZtOJFjMMHvb5ZVm1z9Wt3aXfRB57i0MtVfs73YtSnLcbFUi8F6G8+/YpN89iSDLgpcIeRT5w9qMrP4Gq+pD168SBOXc5NZyQe9BODYklcOZPw9DAqocfbWW5NlNcY51sY4Zu+6TRjMgaP8seeJ+oAmYt2Dk5x4wGXI7XdC5S5MDqeHOmeM/2c622IwLWBewNss7P5cYJ5+JHpcDPXJyQ22Z6SJCgOAsk7enrakB0MNiObjiJIzZcYecK0oSjmlQSRhQenCabaFoSSDeoWCd3ItBFKjGwi5ulDY7P29sYDhY3RX5JyuNs0/IwlSOg125ocgU03PNHhSYZFp8+hyUa6wpwuCvl4kuVtiraLPgKYLnijxxc2+MJesPMNjGyUaGwadLLB26A8IHkb0AOSn9jJU9DSMz0sSLYp2YWnezop6C1kfvXWxaKno2LBW0B8mn/N41ebPf4w9nZDn9jhe5uzTVKNt4tuPaHjDTeY0IUOsEbnIdImiidb/VIiCdaPX3qYO9vmHg76HZTwE5/0k+jzEf3oz4fG6SxpoQubjcNffErczbE+6GhzsS7EJ19oe/Nu07dhOeSsC5untyrGFXi72KbgZYOy4faGhk70d7lHS7b4aA6dbZ50FTNiHibuYYeXN1ja+JirJhtPtTask5Fu4q7YKZbwFAv0KAbpggcbqrs3L9n4inHzYMUectHqpxsa/eRYS3CDPx+zA878wIfWhjXh0KU7vubDwxp0j3cl3fSjd5EPQ7zNERd8TGc1PcS0uBVDdAsn8tI5GfFGG2Zo+F68wY6fJVpiDY1xelo37BSn1hd9xZbPlsQkOj6hDz3UknV6e6tu74KXX3v8++bFBGxd1plkXQxKTtiH1lxtMU62A9gFd3rCWhzRzx4ZjnjSQxuGdOZXGLq8aDAPTmhgrYSRuXR3UFtn9i8vfpwHdOpzKTzNJVuxJ+HNDn2wKY7Q2g+dXfYtDzU+lxCv1qF5nQf5X02/7OILfeaQZc8Ri/QWc2TQT5IhafEJjPjw6w7844MeRmLJfuClUb8Iepsrbu39eKAhV5+kW1yYCzsxTx/36Qw79NkNA2eZt6nsF2fWQd9Ro3XRLZ34LH/SwVtNMcVuccbfYpV/xIN9DZZkGhcfajFjTYpdciVhZONv/eCnnv1Of0UtrvHMFnSu9nI64iV+xRW/Wk8SPXTmwUU88wmdfKvtExyxy3/mKejp6by35u3jcJVzwN3+iR+M0Cpwwz8M3c968w9cxQicrFk4kAlDmFpHZKHDF3/3/KyNZ7V+bXEq1uimLh7ci0s0EmB/4VRc08+ah42zGa7OMb6BYXgmWx96cmBHX35CBwO48H+5IHmSbp8XeVPPVjL0k02W3Eb8Ofv02VPgYX2IAzIl62JVjij598DkLOcnPDxc8KF9Ty4KQzoXH/jutux5og6MLg7NqQVSfYzgaCUa8zIUUGgCWMC5OAnA6Nr48Glzzsl44YvOweOTmjaaFpz5Nh60gLfx4i/Bknx68sfXzy0Wm7cL5khS6GIhcqog0qavxeAgcG+uAE8X+pCdLXRDx1bztBX24FuC2Ty1uRaXezQu9wo5LjzVaI25tC1ENrGZLTZhySx7BXqBT77DRdA2X5/xaPCzQGwm/UTX5o6fRUi+xQsPsvESxGr99ESXP/BWkkkGTLTJ11abF1bm4GEBlRQ71G04NmwHls0CvUVl87CZ2uzEkU3cX0hycNg8+ZY9FrrFawMlw0GNL137+a03OnQ2z5srmyBb2c7/dFW7wgw9HNjSpU1HFx85jGxqdPL2hR3sw7t/1YIf+U+sskWy4a2+OLYx8qHNi2wbiT76+EzBmwT3cOIfMQxnc8ViBQ296Qc3/rZReXNFHlq4skOhf/7Sly/p6nD3EMNfEhRj5MMOT7ytUeuhWCC/AlP400e/Cw/y9ZnHZ2LB5uznXDzb1OOD1jz84mWdkqmtZDcatPlGfzFMbxu4vcGLAuuSP3zSxCdiCEYu/sHHmmE/Pn75gFH82IZGoUeYdi/R8E0tudavPU1CW6LI95IsvhTnZNHflV/IIhtvVxgYdyD5mRcWXhDAVdxYK8bTgy/5na8kOtaQxE+cJdu+JJkwz18WRwcTsYa/WLJ+6DJfdCohZm9xSU9tMS2GrDOxDVcP+/ZlvmA3ueThW8lOOvMRW9koPux9JXPo87eaPuw234Unm8ixP9sXomczDCQc7TtikK/8PRCHPn7plb/FnXtxaq9Sk4nfNjba6UMuH8HAfHLEvj2ipAPW0Ul06GxfEbNsx0tMpJe5Hirp5Cz0UCWx9y2/fQ9fvpbg4Gv9xtcDnStecGLDXPjf5zB+RZDQopGMimNxhWc2qtFbJ+LaQwefk+liC6zEhNgiN9li3xj/uGenmCNLfMgJ7Ptw4yu64En/YkA9448H/fIL3PQp7u091ouEDm7igE32In4SP+lnHj7iyFlITz6ha3bwjwc4nzjyrXFx7nyyT3em0NEcPNOHTu6NiQE4eghztkh2/VJPvlgQP3Qlx0MBn9CVre7xSW983RvTrxZzzk9npQdpmNoLvfyxTsUN3mr2mkMnsc4PsPPiTmIs58C/wkb+ZS9a5xaMXOKze7bwt4ut9Lbv8isaRZ8ixvnJHkFn8vnd+eQMoXuft4kr8+hkL7IHiRd7sH8VqfjgEzb9uGVPEnXKKnOQWOgMArwFImBzNnpGC2ygGdPHKRzC0Q4ChqvxEOjGc4DAVTid8x0mkhubOF76ySuYOEzQ0As93dB6GsLfArAhOEQ52GKzKXnykvCR6wCROFl4ZAhm+nI03fAgkz36ug8DcxS2CwAXWsXY7Gh6tijbiG2QFqvFhScb0CmCM550Id+4IHcQaQsyB4YAt+F52uwXBbTkmdvCDENz052O+ISZzcTh562AeTYBiSD/8CP9bBA2YputMfhL5vnePR3dkw1T/OEajuRXYKqQRSdtvuHb3grDgp2eqN3TATYWrDb8fZ9vc5Rcw8JlkbPFPPPZaFO3CPmeTW24FrZxBU5stXjRaZNJL3ab3yHNTvNsCPRHy279Ehc+sFnauPqFQCzSH1beivW/q4atw8ebPnxtQLCDo03eZmgN8QGczWGDGBBHMKa7tWieJNOBlW7sg78+csSLzc1B7YC2ZthCNt3zmbigM5nu8YODv+wj7tgmuS3e6Isfujn+3OOJlwONLMU8ffSGG7vEjWRV0oWXGKMT+TAtxsRMMQYbbZe4YEd07NbHdvqJHfGvz3x91qaN3VtQseNNq73IHDU9xZgDDG4OFLrSx8Fgb0QL+3n9sRtdcc5mcn0SIs7gL3EhV9vagi2fo2MXnjBi/7yG8YKzi91kWBtwU/SJNQerN378Rn+8it1iyp7Lvh6+8IILP8HICxA6ms9Oa0yNr3XGfhgld9xsNmM92rf4Hj+8rCFvXtnID/Z0ce/NKKzYIP7R2NvFC0zFCH3Za65x9/hbr9YpGfzengoDmLHHPT2tIVjAhky0dHDgi8FiXxzwhzFJDPslSM4TNIqajuJVsSb5VLEnFIe12acUD+wnU5zj78yyn9GJjc41MWa8N7vOLtjDybpMZ7zhS6YYpys68WCO9QpXDzjeVMPD/gHffMff5sAM5njPvqW3Qj9nqn0VhmJTLMC+mKw2B072JLHNZvu8ZI3OfGY+2WLDL3RwEIt0Zidc2UUX8+1X1pCzgv895NLZGBvt1zCgT/qzlx7iX6ywOT+oXWjEmZcoZFqTdDDPmocHXMgRGx6GJIPOSzXfsQkdHN3DgR72XbrYZ8QQP7AZjViZddFW2ICmeDaffXzqhRocPaiYi5ZPOi+121fhy7a5ZK8+ttkDvTTw4CTe4CQ2YOsFDBvsE3iZ22VvIAcP56mYhBe72aG2bsWKGOBva8pDkDHnFt+yEbZ8Kwbss84p4/BFa5wd+NKDXA8n9kpta9t64VvxII58R5/OeFmr9nT4s5ONeNPLHPfpXVvfbsqeJOoUAX4FIIINaGrBB4SUF2CA8S+ACAqGKxzqn7OSQFh4gstmpg8A5nAMPg4hQLkHNhkWgH4lgMjiEImPBQxwvPDuKcocOpNjk0KHhs7aAshGZpM2lmM41Rgd9TukLVJtctnTT96CSECRo49O3nCi0UffLliyS8BLKAWvhQ9Li48uAobdaBSJMrmCOows6nRyb56At1lImOGXbEGIN5vDzpiNKTxhgockFh1Z7CdPH1ssTIexw6yNlH9tNuwV+CWIfOBQs2mwQyzwjwcjuMMLf1iQnV7po9ZvHtvpJPmxuGHMX+ThDQe8xSS+FqpDh24Ws02bP3ugoBec4IZO7MEL5uwmo0IvuHhrYEOQHNOLbDZmv4PDvyIAC/zwIFPc0g2O6S9J8q/R0I3v6cwm+jmE2cw/NjuHmHl081bCWlDIEuN04F/9bCJbnPKVWh/ZeNGNTkp4kyP22McXNnvzzIE7GXwvTt2rJS/8aFzs64ODnz+tbTzEifhiC9zIpkuFfPL4yqducC1JYxNfJrM1ar3ggRZfdNrhg1cxLC740vpnM4zQoqG/9WCe2KEL3DoQxLcDhg/pwF9keYtubcNM/IlJce/h3iEjLvgBjRhT+AwdXOiMxnyF3PyQHf7VBJg63O0V5OOlDw5iiT7eXIqb1h2e8Wpd62vvhoPY4uv2H4e7tjHxBAP8YAcfeyYfSwatD5iQARe+Kj69YBAzxqwpsWqeNZIOxtgON3/RVGJiD2lfItdc+DUPZnzNHjytD338R6bkQ9zBpvVovaCz5u3T7DeOh37+Fw/00gcLsS624Gm/grlLsX7xIcc8cexf5XAm0A0m8MOHjS737O9fbxJP7MSTfIkArMlDS0dX99aZuLQ3iBny6SoG2WCuOMcPD2vdvfgV82KHPHgal6jBB8bks8X+4+FB3LGLz52j1jrf0JFO+MKnteRs4jcxrR9NsQxTupqjnyy4ihdjrgqcFDzsJWJbEsZmMU4v9rDVOmUvWrjDgc6w0LZ3kYGHXwesF+ux2DEXH/FKLizo5sKHbdYTu5yhCv1hnt5wFG/WiwcZNtLRXGuDz/ATv+KD//kTrvREhyddyVesBzR0yk90LA70h5OaTLzkA/SylvgZP/3OMnIkouKSbTAUB+JWce+fnGaHfYoNCt3IqO5ebFtzfKLQ2WUc3vjwOZ3DS22voa95bEKDt2Iu/TtvPQDRm7+M4WVe55AxcsyX2+DLp+KYr9tv9Cvo2KW/vbM1ah4fkEMGW/TBAoZsgt8v/uIvjnH7HH3SG+/sGJ27+OMcZ/6oM3bBdJuECMaoGacAEKgWM0CAaKEYF+z9bIjWgjZm47QIzRWUNgTJjT689QEWeAJfDaAWPh7GyZh1wdei1CdA6Eon9C7Bag6dOmzQcaoFL8jpgY/gNoZeIJFNL/2chzdbLUZzbIjGLAa86EAXvGywFimdlfTGowI/Gw1edGavcRs7+21QdChBZo9AojN7YIeebBcZeIaftgJzvM2ll3v2sVVxT3d6d+jSm4/UfIpvepGJXjFOr+ajU+iNTtuYDULbJkcffrGx2WjiR18XvfzF1D/7sz8bvH7jN35jbE4wMs+GDQN2wM5bJzbAgC/Q6ZcsuvhIH1/Sle/ppB9W7EaPR7FJf4U+9EWHBhb0IxufNkr9sEMDY7qg4V++orfYwZ9v4YIv2XRLNv3zG158bK2RZbMhjx/EGR76+YldeKQrvuSwwxx+ogNZ9CIDBur8xEa82YfOPAUvdDY0tqFh6xz79NBmq3F4uMjkK/PoEK6D8aFvfdlCJnxcYUkfc6wjfOjR4ZstdEfHdutSv7XK72TiZ8w8utETP3rwjbnwQEcWGv2w0a+YDw/80RijL9nhzWZtmJGLnh3hwT/m68cvH+Ol1MaHTnyLH3vwMx8NuWyBPxvYYnzmaZ753ub5t969ZfMw5J+UcxgpcBCLfJM/xZu29UVP/oS5yz1dw4Kd+UScmauwkXw4udBrV+jFP2SyhQ30EPdkR28cdnijYzsMrCtzjHuAgL/4109nuvaQGKZ0x4M+5IRX2BvDD+7qsDSfD+lv72QzeWzQ76IfH7CBXhU80fIVnrDCF070YQuc9aNNpvniD0b6xaAxl/s5vvDCn8105VO66kcvpvEXK2ybY1Db3kKGdQ0/PGDOvvwNU35xsS//aXtg0pd+xsSc/7jKpww+5fLPF/ZwyzYyXBX6wtFcF8y08XXxFZvpGZZ0ggU70dO9ta/N/2rjClzwgYUxNtKf34zpC29+dC4pdBMjZNEZz2LEOP30wQq/9gf8YW4uXdXiBB2sxSuefonyzxD2+eMf/dEfjYcl9sB0Gys8YOAyhpd4pkd+z3ZtNGzmdxjClZ3ii1707byhI/rmuUcvRszRT2d0FTxgiMf2mJdQ/Mlv4iQ5zcUfLzLEL1r2KWwnzxi+5SGwh625bFbMw0esww0P+53/q8GvkvY9f1fGSwl8jePjIsMFG3sDrMSJ9SqnIN+ZS7652d49PXZT9ixRpyCDlJRT6zNGcW1XtGpXgHJY86PXjq7a2HaZZTYnWdoAbR4+CgfPOtVfHZ/aBVpt49kcLRqFLHQuNORkkzZbtdMpPbbxqo1PtPijF7wWmDLb17g62fFPJ21jrpmv+4J/7m8enu5nGdHhVYn/rHfzmhtPtBaHRaBkS3zVzUWr2NB8T+t/UCNXguEvrFnsaPWJq+i359fGq3u0yRxCpj/wQ+dC48re7msn0/Tu1cmJbfFezDSOdqYvVswjC91Mo41Gn/FKOtevVtTNUZszz6sPrXv0rvjVl5y5jkbfzNN98qPR5z7+5nRPRsU9usbN01d/fI03Fi2a5DRnljHPNSc55my30eIxY43eJdaMzXvELMeYki9nn+sz3j7YvDFh64/4VBuebaBL7fiyRZ85jakdYN6YPupRjxqfITiw/Jvk3vQpYbClwmE740km3sluXn3Jx6c+c2EQrblKPOk+F3TRZofapXQfX314xpeseKdn/OuPr7arkgztWY42XvrSLd7mk9m4Nhr1zKN7dI27r12caJurVrpXuyrdV+NvjlofGcnUbjye0WhH5z7d3KeD++3SHDT51735igdu/3KO/1Fakux/u/ylX/qlkRCimWl34q2PjO1inn76d6GZ+9MhOeiTZ457dfPcb8eNMfPwiFafdnqpu0czx/I8b6aLb2efsxA+Hmr8fwYSS7+S+VeS+qTO/FkHPJSZr/GuxrIzHfWjCRdtOusr/vQp+rYLftEbw7d5yZjnuXfNuMS7sebVr90Vr2jm/uabRy+FXcky7qHCZz/+7wlJvbyh/xk9ns0dDA7xyM7yCjkI3trRFy/Jn/WJ10719x/fdxo9AX0zSJTM0FjvpCij0OVM7TmAzZn74mGO/rmtT9t8pba+mV7gtwjQ7cSjOY3Hb5aJRjsa7ejU6REvOija0WqzfbZ/EE1/NL+5M9/6POEpZBh3mUe/WW70s3x98VTP9PXXtz2en43HM1ptV21z5/lD4UN/JAc9ni1299t8aoe9uX6y8r2h4m18b+e0k39I1GFbG8Ovkh61o1HPdNpo66sOh/jod23rsN2PPpp4VetnK5rwmPXbpkODNnyMx9999PHQNmenYp6SbtHMPOZ743O7eTMffdGoG6ueeTR/1mGmi3bmM9utPx7NU+urH41rLjv1hdH2XPzQh3t084Ew859511/d3HSdddq+p8dOvNKvMe34JUc909kT/ZrZf+piDfXWtDnkd1+Nh1KdnGr90erLvvrV233o9OdH490bm3nPmMRzm6Z+fNJFnwutPvdz0Tdf0au3+82rL57R60/f7uexZNanHR7pNtPEI5nJQxuPdFHXp57nascj/bb3XG24z7hpz3N3kpW+1c3Hzz15+Ehq/Erg0w9tD4feVqZXupOxXbJ3u7+52TrPnfVunr54hYOx7uMTX3V6oYmuvh6wkzWPs3FupwMZrnikc7Tp402tT0R8GuLTHJ/PhG3yZh7mz7yTN9PWh7b+5FeTsVNBH3+2uUfr2il2kpGceGrDrZeCeCkz/3lOelXHZ9YFffY3tz706estv19wfMZFZ58r+uVBwc8cNV5KvGqPzkO/lsx96RJ9dLupz/I36pTKMIoqKdqYvoxwDzBjGQmsgFE3Ht85MOONbr7XnmWPxvRUVSBFVx1dbTxnvo3H2xjanO4+evZs3wtEZScbsn+bFx7xil/64dW9GnZo8J+Lvubqx6954atd38wnvtvz8Is+/vGYZenbaTza5M86ke+yeJuPbrZLPzzr94uCn93Q+DlSkqGQjTe6eCVbvVOZ9T3WeDyqs6e22hXP+Gkrjc80xrRnv0ffnPg0X5vs7Jxtnnk3f56XbskwFr+Zrrlj8BC26RpdPKKJ17YM+lXQGE/3ub/7bb71x7+2OlnbY9riimz3rvhWb8+Z+c68o9eXLfVtt2dZ0SSn9iwn+rlvp/vwwiN+0c197mvHW9t8RZ97b4X8xOvtup90/SLlIGtczbZtfnjoq6CrXa1PCZtkN14/mmj5qjY6Fzrjs4xBNPldOzpzktW82rPsZJqbrOhn/s2Nf2PNb2721FZv8zN3nof33I6HfvM7N+x78VIbU6qbl27Nb47+I9nRHLzCXwwo+pqX3Hiqoxk3E47azZv3cH3+jpK48yuqly360JCZPfGu3on/LDv7zXfVZk9tvLbH4zvXs0z0yXFvLN7a/OKBN77NnWXVFw1++uqfZScr7L7xjW+MT2TI8eu5NUp+/mnurFuykzPLjX9jzZ/1IdscJVtnns2NJh7pbE4ym78TT2N+NejMJyMe7pMT/2150dRfXX8y5/gjs09b5A/m2PPCtbn63aPHxzXbQqfa6dlctN1XZ8OR6rM8USc4gLbvUypl0W0DoM3gNgj36PXrc99m1fz4BpR+ZSc5c1/ztumbW/9OdMlWJze6HENP48k0Prfdo53LTOu+Nlplbuub+dHDAlbIjnd81M2JV30z7WCwpavxfNG4Gj9jswz3lVmevuSl94xdffGsHT+2tcj0mSsmXGFNl95opEPj2YBvusS7trHG65tp9M3j2oo+dK6Zx9w/j8Vj8A0zrwAAIABJREFUm3c0eG6PzXLYEhb6WxvhGf9qvOJXX7X52yU+5KAzV19z1N2bG/9tGY2po29utHNNXmXun+e7j45O0cW3+drGGlfrg9U8L/ptGXO/+/jgodDBhVe+mPWa5+hPH/TNT6fGqutHm7yZ32AwxR2aZJubrvGJR3U02vWp9ZMZr8ZnfukUfWN0qm/Wr351tpsTb/0lOMk1Hk28qs1Tkls985vH3TenfnJm/vEwrmg33txozNXHlvoOTfshOfqjRzvPmfUNF/T1p6N5yamG19zfvPriUXsed6+kVzqZE33zD5GOfvRKNO7RbffN/ckwRyHLnPZk/a3HYkCypr+ErfFtuclWN+a+9qzHbONQ5NAfeKNPlvvKzAv/xtwr2uzLd/rnNpr64qmOxrwZn5lv9M1vjn44mWvPcU+P+cxLz/Qyp75kxH+mqQ9t9Pq2aehS2eY3z20e+uiqZ7vRmaf2INIDWvPJMm97bv3VxvFJv2zAp7H0nuegb84s0/zkzrzc18bHXHTm6o8X/+hvPJmzDke6P8s/fUmZ2ZjZqCMpFn20jKwvwwERkMZmELWjm2VEk15qtPPijz6etefamILfXI/Gof5o6JiD9M3tnKYv+upt3vpdsw3k1d+8dKguQIwnh1z3zY92rpPfPG33ahuBe5cSbfOj0+4+2u0+c5uPJjp93ef/DiRt1068Wtjmh3V8ZznNn3l0jz7a+tInnfQr9W/f///R728q2/PSqXnJ0z/752j8oxO/sz14Ji9++CSjcWNzX/3qSvLVxc/ME12ymjPHtXmzjJm2/viZT0Zy4rdTbS45c8HHNfN1j5+SHHV9cKsfrUv7WGWbBr/t+clAaywdjsX7WOMzv5l2W6eZrjF19+kz69ac+tCwI5/Wn235oPbMM9pZR/f1q9Nn5pO8dGl+9OmSrMbTwfhsY/Lipx2vWZ/4RFdbrS+eMz8y49X4PM/9rJc2+u24m+fM8pM7y0hmONiPww+f5pszz0v23J/c+naiz67tsfqTl53p0Hi8jeuLHh297ev2bfdoXO3j3kgnN12jq12dvOrkzjL1Kds66Jv1m3kY2+Y1z49/fOMVP/V2iX9z2ERGcxrXr9TvPhvGwBSbvb1vTuMz/axrvBpPpn73+uc+/TPv5iUnG/TPc2eZ7tkyz60dXbU1gg7f5qVzOkabDttykzPjF49o8Yifvpk2GrUrulluY+rmOpOjb456Hs++wfQof+xJoh4IKU1RZTZUe7s/49FtA8BxGZx90dWuTm7t9Jnr5iYTrb5otI3N7Znf9rzm60/P+M11dPpmHu4bU2+3x+D0R3J0wWYbH/zpgS75aMO8haAPTfKqE5WeM4+Zxv0cfOiU5sW/vsbNm3mOSYd0oVsFXXjOtf7ZhuZEg7c+urkaT6b5lfq0zW9s7nevGJvvtbfp53ZzxuRDf5g/08TPsPu5PdM1rp770c96HxLzQ7rWv13Hq7pxfPW50qs2eUpzjM/+iId6nju39W+34z8Gtv6IPhpt9zP/WZ9t3s2f6+gTFT/teWwnGTPNPD7zKu7Ca6aLP5ru0027vllOvNXRNp4M8+axxud61qN56YpOicb6qT3X7o8ma0ya/ojfTnPImB8+o6Vb9+a50jfWjauNRaftvlI7ev3ulZku+rnPfbTV0W3Pbzy/7qQvfl3omzPLbF5j1cmd2/N949vz66+ex5uf/OpotdFnU/TqaN3XX5967sdPXzGl3ZxenmmnG9rth5KZd/rRKz7Gu2b++tBsj2lH13181dvz8EjH+KnjUR2vbBkEh+xN32jiqZ28+Mw1Xj3gzP3JNw7b2mhmfsnTr9Tepq+fnopxffWr9TVeGy0daqPJ/pl2MD3EN976igt1spLfnPg1bn4Xmll2NM3drqPdnpdO8zi52TDTRyN++SYb0MYHfToeS6fBey/+eUaCFIrNpfasqPuMB8RONDOPme9MO/Oc6aOZ+6I11v3Md+6b57mfwU/fWcY8t3vj5mkXZDvN0Vd/dMnXH7/6qr2dwN/TdUXbtR3wxpMRP+2eBsmtP15HmpNOO9HPc+f59ZuTHvrioW8nrDrEo5t5xsvcfIIHXGzy+rQbi14980u3eO9knz6X0txqMurXp51csrdLvNC6tOOBvr7o0l8d38bQJnuWAzclfo01r7Y6PeY+dI3V39yd6NO/MW30tef7+FWjRadUNzbL1KcdXbRz33wfj2qYzHhEG7/o1I2R4X5uz3SNb+uyTa8903Sf7OiTTc/uZ9rtvnmesW3a6Od6pos+/dTxNDbfz7R4VOqv3Zzaan3ZVP9MF4/iaKaNLprdtKNNtnruS4fGZ55Ho5vnRWfuPN+9sXk8+Y1pz2ske+M1t5s7y57vzWkNmReP5qXH9pzajZvXnMbU8du2qXkz7U73zacbPbMtWvu186qx+JrXfbRH6tOvpCNec9t9NPN99DPf6LZlD4aH+KSrmu7HmmPuTjrNPN2TiVf8a+tzzdg1Fo/m125O/dmjv3tj2tHU3pZVf3QzD/e106n5arao55xkey/eCRtzkjdupj8am8f1dcEpG6NNt+aQGc5ojDcHDR216b1dotef7mTq11bP9m7PP1J7T75RP5Lw1b8QWAgsBBYCC4GFwEJgIbAQWAjsjMAPv9bbmW71LgQWAguBhcBCYCGwEFgILAQWAnuIwErU9xDsJWohsBBYCCwEFgILgYXAQmAhsFsEVqK+W6QW3UJgIbAQWAgsBBYCC4GFwEJgDxFYifoegr1ELQQWAguBhcBCYCGwEFgILAR2i8BK1HeL1KJbCCwEFgILgYXAQmAhsBBYCOwhAitR30Owl6iFwEJgIbAQWAgsBBYCC4GFwG4RWIn6bpFadAuBhcBCYCGwEFgILAQWAguBPURgJep7CPYStRBYCCwEFgILgYXAQmAhsBDYLQIrUd8tUotuIbAQWAgsBBYCC4GFwEJgIbCHCKxEfQ/BXqIWAguBhcBCYCGwEFgILAQWArtFYCXqu0Vq0S0EFgILgYXAQmAhsBBYCCwE9hCBlajvIdhL1EJgIbAQWAgsBBYCC4GFwEJgtwisRH23SC26hcBCYCGwEFgILAQWAguBhcAeIrAS9T0Ee4laCCwEFgILgYXAQmAhsBBYCOwWgZWo7xapRbcQWAgsBBYCC4GFwEJgIbAQ2EMEzr2HspaohcBCYCFwYBE488wzNy7lHOc4x7jXPuc5v/8+ZO5371K++93vjvva8RiDh/743ve+N+7igS/++mcZs8xZn5kXecrM41znOtdhvY3hS1a84xWfdNXvSi91Y3iQhQf+8Yg2Xmp92ZjM9FDXN/OIPnnxi3+06Rdd47V3khOv6njVVje/sfjSy8Vmeie/udrGjcVDu/t4f/vb3x5zz3Oe84yp8a+OLozn+cla9UJgIXBqI7AS9VPbf0v7hcBCYB8gIMmSfHVJmObEUjuaOWGluv65zEldc7YTMDTf+c53RiIYj1meBI8cNHhI5CR75z73uX8gGcTHeHLiMcszpsx92nibj6cSH3IVY67KNp/Gw6ZkE717/M9//vOP6fFhl0IGGsUYHl36zHXpSx/9c2JsLB3iX1981fpqdz86Dsme78lkZ5g0ptZPDn1mPvrnNh5s05deMzb1qb/5zW8OEeTNds5y1/1CYCFwaiOwEvVT239L+4XAQuAkIyBh+trXvrb5wAc+sPnoRz86ksGLXvSim6tf/eqb008/ffPFL35x85GPfGTzqU99anPhC194c+1rX3tzkYtcZGhtrkRNklWSnDklZLXV+qKTtLp34VHiOo+//vWv37z97W8fLG50oxttrna1q20udKELjTlzImhOuiDeSZ9Zj+6TW6JZjZdLWxIZHTn66FoyCp+3vOUtm/e85z1Drnl0POOMMzbXuta1Dj9cfP3rX9+8613v2nzmM58Z/PC5wAUusPnWt761ucIVrrC5/OUvPx5G8H3HO96xee1rXzt0gPcNb3jDH8BcMqzQJ9vxS7fus3OujWWfWsGPXp/4xCc2PUyoPWjQ63KXu9xhFubAAx+lNj3wefGLXzx8Bjc+u9nNbnaYJr0k6Gx8+ctfPnjc4Q532FznOtfZnPe85z0sZ90sBBYCBwOBlagfDD8uKxYCC4GThIBE69Of/vTm2c9+9ub5z3/+5rTTThtJ5n3ve9/NBS94wZHAPetZzxoJmKTxt37rt0YiOr91xUOCKVlTJHKK9pzQoXM1VsKHzvzGJNoSxVe+8pWbxz3ucSOBfdjDHra5zGUuM5LbEj61OWo8kjsETH8kt3kSSn3kNN9YJfra6saNpbd7ye2TnvSkzTOf+czBD35wuvjFL7655jWvOViYK6F/7nOfu3nVq161+epXvzpo4ctOifj1r3/9kdhf9rKX3bz5zW/ePPrRjx663ete9xoPKB6a8CFTydYwnvVDM/c3Rz3f4+Mh7a1vfevmRS960eb973//0Ocb3/jGqD2w3eQmN9k88IEP3FziEpc4/KadbPyTEU8+fOELX7h5zGMeM2Ln4Q9/+OamN73psDXMzJGos/GRj3zkuIfDVa5ylZWoD8+uPxYCBwuBlagfLH8uaxYCC4E9RkAC9ZWvfGXzzne+c/OSl7xkc77znW/zpS99abzllahJ2t73vveNMUmdN8ASXf0laJJTCZgx/Fw+VXFJRF3GJfeSOfMllu71zZ9A4OHNqnF0n//85wcfb6TxRUsumfijcxkjJ/nJk4wbT+90JrdEXV/34I9GnU141G9uen/84x8fybck99KXvvTmbne72+Ya17jGeKBAk41qb9Rf8YpXDBvQGmeft8veWns4ckny8aCTt+18otAFn2ykkzYcKniig8WsLxptF2zMhaVfAp74xCeOhw08LnnJSw65xvDxIHKDG9xgc5vb3GbMzZ90owc+/NW92oMff9EtWeTiyafiS/yoP/e5z42HBfNWWQgsBA4eAitRP3g+XRYtBBYCe4hACagkSsLuba83rD5vkTB60ym5knhJ1NGje9Ob3jQSOW96r3e9641kUbIqsZMUmudTGZ/N6JNsXuxiFxs8vvCFL4xEWxJKhrerkkKfgpjTm2hJp4SQzM9+9rNDL7wleZe61KXG5zl4Sh59mkPWl7/85dE2lw0+3fA2WFL4oQ99aCTGkmTzJZT4e4tND3Mq9DH+4Q9/ePAMJw8IeLrI7FMP43S5613vOvhJvPXRjQz2wzgMJb5o+swFBle96lU3t7rVrYa+3rKbI2FXw58un/zkJw8ntrAw5jMl9ijshIMHALLpwLYrXvGKQ7/ZRn7wht+bfny9Pb/3ve89fjERB+HF3/jwAR/jzSb20IGOMHWPv7oEXQKOFyx9XmUufu9+97sPP+zl47Bf9UJgIXBwEPj+rnpwbFqWLAQWAguBPUPAm06JuFrCJMHqcwjfSXurLkmTcLnQSroe+9jHjs85fLIh0ZUUv+Y1rxmfPki273Of+4xkXSLoTb3kTbLoDaqE0/fPt7/97cfnLE95ylMOfw4i6XvIQx6yudKVrjTeyJJHH2/8JfwSUcm45PSe97zn+AYaT5/t0Nc4W+hKd99IkyM5fNrTnrZ529veNt4Q94mJhwXJKVpJZjb6Xv8FL3jB+I5aQkt/fCXqPue4y13uMnBAI4mGG10l3Pjc+ta3HrjBzjx94YjXLW5xi80d73jH8fBBZ2/a/XLx3ve+d/B63eteNz4fkcyzH+YS6je+8Y3DRnoofObzmLvf/e4jcX7pS186km9JdcVDxZ3udKfxECBpDx8JtMTbhQ9M6O2tOn0l1Xyln44eSp7znOdsPvaxjw3dPDCxGx73u9/9xic6MFCy1QOPhF8M+JTJww0a/sB/fZeel1a9EDiYCKxE/WD6dVm1EFgI7CECkq2SSUmaN9uSwze84Q3j0wvJliL5ckmUJZb9xUi0/gKl5FayLGm/3e1uNxJ1ybVkXXLWXxiUkEo80XsTKxGW9Pk0RCLtbXzJIt0kwt74ku1tsWTWJxvelEsivZ196lOfOhLO3hzj75cB8yThEltJ7ste9rLBwzwJJ55k9FYXDuxju+/O8fCmXMLsO3OJKx1g1F+49ebad9bkSMIludp4aSvs70FIjcaYN+J0QwsDF/l+sfAw40EDzr4h9y28RJfdV77ylYf+kmy82Y3OAxR86cvGsDOGtweRfJme/CURh+vznve84Sd+Ybe/EMq3/lLv4x//+JFss80Dmjn84OGErg9+8IMP2ypmfPrCFg9wT37yk4cv/AJDrnE2wz6dxuT1x0JgIXCgEFiJ+oFy5zJmIbAQ2GsESlTVEigJn4S6N63eovZGmW6SKgmYN6ISdPe9hZYwSgwlovqr0UlKvS33WYu3qJJrn334ZONBD3rQeGMuOf7gBz84rviqJbP+gqbkXzIvQaSfTylcklr9kj66+9dh/Ess3uRKtCWZkmrJIb3pKNH17bV/mUXia64ieZTk0wVPSarPWXyKIimVLKs9kJDlTfXTn/70QYfmoQ996NA329XxxRtW5Hu7LImlGzmKt/suuBhD7/MS38F7MCKXf3yiAksPQOzztpqOHny8iYeXz2gk+eS74MeWkmP+ju7GN77x0AOW/iIoPOhBhjGfNvnFwl8U5Q+/ZPgVAv0jHvGIoRcMvFmfbSXDg5qHIw9gfO/Nu7f6kndj7FtlIbAQOLgIrET94Pp2WbYQWAjsMQISOknazW9+81F7Oyuh8sa3RFbyJdmU8JVMU1O/SykhNe5e8XZWIufylhsP9JJbn214++tfOpFIS8T7vtpcb2sl1D4X8dZaciqh9wDhLbDPYnxGIfH0ttubY2+ePRzQAU/8erstAfX21ycheEscsw+9t8+SZ8my5PK2t73tSFi9eZbAewBggyTTm2c2ssXbYglxJTy0YUsHdntg8AAk2WcDOg8N7JOIk40nnTz8kOVNPjvIpB892cg37JX8o3e5l9STRT+fEeknR63g71cBibhCF/9cIuxhKwn3z2N6aPCZj0SbrhL4O9/5zuMzGtg84QlPGPj7tULiHW/2KvrYww4PNniRSw7s6T7jNCatPxYCC4EDg8BK1A+MK5chC4GFwMlAQJI0J3ASLJ9N+KcQJeku4xIqiW7Jr4RPIihxLOmW/LkUfNB6S18iJkHrrbFx/RJvyaTkFb35+o1L7vD2Bt4lKfUgYQ6+xiWPvsc238OA7+PVaNmg9pmG+fiaJzH3xpku6Ubn9PcLAL4Sa/zIxNMbaZ994MF+vNUufMynrwRUmXm7N6awDRYSe8m/hxUPRz4zIUdB6+pBQ5KupA9dJPfXve51xyc5fOZhxkOEpLtPdOjqFwY6ehgyP/7w9rDCpt6eewiQpPN7f2G4xJoN+PgVpAcctuiDmRghT19+hGGx43MmeirowmN0rD8WAguBA4nAStQPpFuXUQuBhcBeISAR7E1vSZbETFIncZSseVst8UInIUbn0pbYGZe4oZH8SdRKMks41cYlt5LFEls80Es8JXz0QVtiq68EHq03sd50u09PiTQafH3u0ScfHiLQSYYlru7TscSdnHSBuXu2GVckoJJkf/HS1dt5PCWePjfJtpJWMrb56jOONwzucY97DD3Z5y26T3FgIKlFO+syPyCQ6827pNxctN64S/rRPeABDxifxniL7S23Xxxg6lMhuNHVPBdZxmFKvr90CzNv1PnZrwfezuvzcERWPjAXHnjrJ5t9+j1AuS8WjOMnTvzFX9hqh5d6lYXAQuBgIrAS9YPp12XVQmAhsEcIlLSVhEnkJJPeNvsfIyXq/iURiZUxl0TTm19vXiWqvtv22YnvriViEmh0kjoJawkZvuTpk8yRiU5BU/KcLP1oJHg+d/Hm1ycYvm+XBErQvRmnw6tf/erx0ODbdMmsxNK35v7CqO/T0SsllnRI/oyBewm4zzr8pUxvqP0FS5/UaEti2cF+yTEe8cHTGNvU2tnATn1oFXr7JxrZVEILA7anG13dk+PNN7zZ47t2eHsw8eZfEi7RhpMCF2/RfXbiAYVc9OTEWy1x9307//oshQwy8SSLPn6V8OBjLhwk5/ztAcanN/QxJlbgzE8whAH/8wO+sCNLbMCXn+gLl2JgKL/+WAgsBA4UAitRP1DuXMYsBBYCJwMBiZVkS6LsXuLkDblPMnxTLFmVqKJpzKcaklZvUP2LK5JBY2oXPi7Jmn5zS2glgBJUMiT9kkOXedrGzTNHYicR9023f11E8u0tvm+rJboSTEmjt8e+qZZMSmTxkogqvoGXROojlwyFftuJNpk+z/BdukTU9+/+11b/6oq3y4o3z+yX/NJbjTed6T4XCbGkVQKOBv/o2EYfeihwCi++QE8/D03ewJMPA/+cpb+giQb+5t3//vcfSbkHKzLIgxPeHjq8gZfw0wd9DwzelsMLXw84xsz1ll2C7Z9+9JdHFTT+OUoY+3bdXEm9f/vdX6LlC7qR4YIN3MWQhyvxIsn36QzfkEMndOkzBK0/FgILgQODwLn+9E//9E8PjDXLkIXAQmAhcBIQkDBJEH0r7t/RlqBLpiSgEilvQP0lyVve8pYjOfbGVr+3q7731j7jjDPGJxf+hRD/KolEVoIpaUSr35tZyR9ZkjOf1kh6vV2W4ErefHftX3eR9PXJhe+wzZfYSk7x8d/ao6OzBNMbZXy8ZZYY4+9tsGTe216f8phLp2zUnpNk9y793gTj617CLPH0Fp1M/0Y8+9hOFhvZTEd/WRYtG5X4qyXVsDTXX8j0QGCuMXMUiTKebPVtPX6w8E9WslF/BWZ85N9j9z+i0hkf8118SJYHFTbDwxw0LnaZ3xzYeYhhN3/7X1L9m/YSfbbDuocSenvQ8sAkSWcPGg8H9PB5jocdmOCHNly97ed7tpGjrcZ7lYXAQuBgIXCOM9dj+MHy6LJmIbAQ2HMEJJDeVPv+WrImAZU0SXYly5Ivb60lWyWXaL1t1q+YI/FTzJWc+27ZW2BvpvEqqTbXG3r0kkmJnK3c5xESVQkffnTCv6TSW15/cdS4f8lE0lrSKTE1Tpa3vB4+6EFfSbpxn+Xgh7eEWaGDRJl8vBT30funET1ASLzTF0+yJb0eVnz+UZGYKuwtAaeLuX4ZoBu96NSvB+SiT75/r73/sAiOLrxg6deN/vIsOfo9/Ljoib/aRT9zyWLz/FCQjfCgFxvIh7+abvzljbiij3x0/MImGPGdRL5PeHxuQ3/zySS/GICleDLHlU3w4E9zVlkILAQOFgIrUT9Y/lzWLAQWAicBAUmbRLEkTVKmT6KnGHNpSzgV4701di/pqt98tPokcy73+vBR0LiXnDVf8hcf4/Sp6EePFz6STvNc2gp6OmWHPmOzzuiVWY77eKUXWemQHujwam68jLvo5mHGvMbQehBiZ7rFhx76tOc57sOWndoVMrKPjHTztrp7NPRnO97V6PHSVzHHZY4xF7r0Z4/x5qBLBzzQw0RNDtpZjn66JMc9erTG6qe/9ioLgYXAwUJgJeoHy5/LmoXA2RaBEqMZgL1KXLZla7skU5VodtJpHitRK7GbebkvATZe0qZ/5jvz0K+tnuXQa56jnaz4zXPSJ7ojzU9eMs2b5Sazvvgk23hy9Zkvse1hIfnxgYGSHHPm+fmg/sbm+cZKfPHCk/5kGpvLzCce2+O10c641Y+3ki7dxy8Z+t27ojGXrjNNWDd/EJ+Ff6RTts36nYViF+uFwNkSgZWony3dvoxeCBwMBEp4sqbEp8RFIrFXyUs67GU9J2t7KXfJOnsiUEJevRL1s2ccLKv3FoHv/363t3KXtIXAQmAhcJYgIDHvOksE7COmB/khZB/BvFSZEJgfgusuDrcfnBtf9UJgIfDjI7DeqP/42K2ZC4GFwD5AoORAstCbvtQqgai96oXAQuD4EWhdtd5ae9ruGz9+SYvDQmAhsP4d9RUDC4GFwCmLQIlBBpS0zz/JH4TEoYQoO49WryTpaOisseNBQBx24dP6WzF3PKiuuQuBoyOwEvWj47NGFwILgX2MQEnD9rfoEgdjEveS9n1sxjFVY8sqC4GTjcAch92vJP1ke2XJP+gIrET9oHt42bcQOOAISMYlDfO/2sFkfV0HHIIfMK8E6gc6V2MhcAIREGMSdFfrz/32A/MJFLlYLQTOtgisRP1s6/pl+ELg1EdAkuA//+k/xClx6C26cX0HpezGlpWoHxRv7087evgtKfdPWerz77j7T6y2/936/WnF0mohcOogsBL1U8dXS9OFwEJgCwEJgv+N0//YWJIucZgTdVO2E9ySWf3udxrf7ptFz/Pn/rP6ftaXnf59cf8rZfpUn9V6HI0/HVz5YKZNv52wrW/23zz3eO6TG49k1V717hGY/RuOfs3yv7Be61rXGv9jav2757ooFwILgSMhsBL1IyGz+hcCC4F9j4AE4b3vfe/mTW960/ifKyWHEj39yvyzvOShhE2tPScUO43j0ZyZdjtZqX1WAjbLZ6OHE78mnHHGGcPmvdBhN/alR58iaSt84377V455HJ2HD3Pr343MnWjCKz5Hkr/T3NW3OwRgyp/+59hrXvOamyte8Yqbi170orubvKgWAguBXSGwEvVdwbSIFgILgf2IgGTsy1/+8khavc270pWuNNSUQLgUiVrJ2nbiXjKXbej01d/c7X70M83cjteJrNODTP9b5uc+97nNW9/61s0nP/nJzX3ve98feiA5kbJ/HF70rcBckXy7tD1oVNikr7r/DTR8o/tx6nArHmbZ+Hf9OLzPrnNmTGEgFj0oX+QiFxkPWSfCb2dXbJfdC4GdEFiJ+k6orL6FwELglEBA0iAJ8xZWkn7HO97xcII+J+oZMyeQ+mpvJxfbbXT61N3Hv0S0drJOdJ0cye7HPvaxkRx94Qtf2NzqVrcaNuun47buJ1qP3fCDUfqiDzM6NqZW4Oa+yzfO868iu5F3JBo6uMjoIWHWS/9+wOtI+u/H/jDtgerd7373eGjks3xDezrhAAAgAElEQVS4MN2Pnls6naoIrET9VPXc0nshsBAYCJTo+Ytsl73sZUdCZmBOGtBU6q+ek1v32/31bc+f5xnTPitLepHx7W9/e3P66acPWy9xiUuM2rfqZ7UOu7EvPdVKOtWOh7akT8JXMo3WvXr2WXN+lDp51eZ2j7/7EyHnR9HpVKaFVxfcXHz1qU99avSvh55T2btL9/2MwErU97N3lm4LgYXAURGYEy73Sm9t3ZeMNVaiEVPJhUu/0v32vOhnmvrwTo/6zop6tiG99bn3L26o90uB34yl+/ySD/Rlk3uXYtxbdfXxlHyS3PlhYNbheGScneaGJ+z6dUI9+/HshMeydSGwVwisRH2vkF5yFgILgROOgOTBZy/KnEiU5NU3C9a3Uyl5Mz7Pi9c8R3ISff1H4tv4iajJJEfS6SoJ7TOEkt0TIevH5THj1f2MZ3zDi//6J/3cR9t49D9qDR/y1fj6FSLePtM47bTTxgPO8cr5UfU6CPRz/IUfjIvPg2DjsmEhsF8QWIn6fvHE0mMhsBD4sRCQNCiS1BLVEsQY1i5Rk1R8/etf33zzm98cJI37fOT85z//SIAlc5I7/CWSrjlBx6skJTl7UdOnhKgEXd/J0GUne+kRTsbd64On62tf+9rmq1/96uiH6YUudKHDCXUJdPbtxH+3fWTChTyfZ/ieX9u/uU+nq171qptLXepS49Ob3fI8u9MVY3B0wbGivcpCYCFw4hFYifqJx3RxXAgsBPYIAcmBZFUC0UW0+5Lvkgv9EkH/Soy/jOnfX1dL3PDxhvUKV7jC5trXvvb4N6HRffCDHxzjl7vc5TaXv/zlR1IZ7xLQneQczfzdJKFHo8lONCVL4XA0uXs5lo5kuqcffb/0pS9tXvva127e+MY3Dr9d//rX39zjHvc47K8SP7TK0XA40lhzyfVAxocvfOELN/7So7Z+vrz3ve+9ueQlL7mXsJzysmDr4ic1v86+blzfKguBhcCJQWAl6icGx8VlIbAQOEkISAokCJJwdUlC/fVpS8olbK985Ss3z3/+8zcf+MAHxltzqvvLqP4d6Lvd7W6bO9/5zpuPfvSjm2c84xkjubzd7W63uctd7jL+cyEPBookRcFfwb9Ec3TskGiiNa9ve+PRfDUaVw8CaLTNIaOLvSWeydsvNX3/H3v3FavbcZYPfPEn1Y577733Hpe4xnGsODgF0i4AARJColwhJCTu4AZxAQgULqJcBQnS7STuTlziuPdej+PeS+w4dhzgr98kz8lk+dvlnLP3Od/e+x1p7WnvvPPOM+v79jPvN2sWO7M1xxhcr7766vDDH/5w+MpXvtLqPve5zw1nnXXW6jEFP3HGTU+PSWSMX110Bx+yAjm/mpjvCy64oC0OPIDLk+5XE+2ia1pwm3Y7+nmAd+YomCee9nGUfYXAUkKgiPpSmq2ytRAoBH4DgZ5oIW3joD7kQcxLft111w2XXXbZcMsttwzbbbfdsOeeezZPuZcHeYnQnXfe2bzqjz/+eCN3vO62ZzinXbzJJps0gmjbTLzxIX288i5kXpktHghlts1oI48obrzxxm2RQIZtaTsmnPREf8YoJpfxy6dujMH6zscWYwr2sVPs8oIcmPSyvf0WIObKuJXDTTsPzZoDY7ctCRG3rUW9c7zVq7PogjFszZ8L7l4OdeKJJ7ajPLfYYov1Dc2S788cZF7NS/LmCe6ufh6X/IBrAIXAFCBQRH0KJqFMKAQKgcVDoCcWyB9v+g033NBI3mc+85m29cKWF4SP9xXJJrdq1ar2Mhfpe++9d7jkkksakd9///0bIbSl4plnnmmEEbFEWmylUG9rhRfB3HrrrcMLL7zQttIgjtJIKs/uEUcc0fq57bbbGuF3tKRFA49v9m2zvSdES50EsT/jgTNiZ4whemLX888/P1x99dWNaJNHuJFwGDo33i8fsITdTTfd1N7QatFl8YOkH3TQQcNee+3VtjeZa/NkfjyDoN72JvL6r1AIFAKFwDQjUER9mmenbCsECoF1QgAJ5EkVI4ZIH6KMDEqnTCfIHwKn/Nprr20vcbH9hdeWlx1x9zZQ22IE+57vu+++1Q+a0stL602htnPYA//FL35xeOCBBxr53nbbbYeHH364kcbddttt+NjHPtbI/BVXXDG8+OKLjVieeeaZg8UDkhkb2eNCNJdLMDaLG3Mj7TI+sYXRNddcM/zTP/3T4FcNWPm1AXnnRf+Lv/iLhpF97v/5n//ZcM4vFerNqe1Lv/u7v9vmzCLLryWIPtJu+41nDuitUAgUAoXAtCNQRH3aZ6jsKwQKgbVGIGScAmnbVo4++uhGvJHw733ve8M999zTiDGizhN7wAEHtK0Re++9d6vT1ltP99tvv0bknSJy4403Nm8uYs4zzgPuNeo88gg8Dz1vLfL+8ssvD1tuuWUjh7y52iPvIYwI/LPPPtu22fDIf/jDHx70HW8v8irEu94yS/yPuUhA0JM3VosWe8rNy2abbTacfPLJzfttu5JtSxZReQOt7UgeSEX6PW+AvFsgkTv00EPbAsm8qTNHnjXgkd91111X4xs7Ki4ECoFCYBoRKKI+jbNSNhUChcCCIID4uZBeMaKOCNu2cvHFF7ftE7ZQIN7Zw/yFL3yhPTiK0Nu6ou1pp53WPLTI3ne/+93hoYceal5apJ4XnseX91cfSCFPO7KtHEm3L5re+++/f/iHf/iH1q/tMX/8x3/ctmP88z//83DXXXc1Um+bBz0hsGIkfTkFxDzjkzY+YzYHtgxdfvnlLQ1D+8rJ2LZiLuBrYYOg2+rCm25BZCuLxc9jjz3W8hZEsDdHPPQWSYj6Rz/60bb1iOe9QiFQCBQC045AfVNN+wyVfYVAIbDOCCCCSKDAw/onf/InjfjxqvN4I3tItAdMPeSI0NvygiC6hDyo6AHSXDzj9j8jmYihPdTO5hYjooildgilvefs8NAjrzFv8THHHNO8wfas02GLBltC1PXb29AMWQZ/jA8WxiaGlTJ4GT9MLXLgcd55561+sBSGyslZ0NjHbs5si6EDrra/RDfsyYuVuQcQ9OhYBlDWEAqBQmCZI1BEfZlPcA2vECgEfn2UIjKIzG211VbDn/3ZnzUPLGL3xBNPDP/2b//Wzvi2j5x3nAcXsQuBzMktCB+iiHzz+Noug2gL6nhxedl56pFJxDNtQkjpzH5qJJK3F4HUH5l4e7XrQxYNfdlSTBuHMcIRGZeHifFaBMEAPra22GvOU257iwUQkg2vr371q8O3vvWtVm7Bc+SRRzbS7oSX4CamxxyEnGcO9CldoRAoBAqBaUagiPo0z07ZVggUAuuEACKGrCF5SCGS/qUvfal5WE866aS2VxkBRw4Rc+QRgcuDjjqX9lZLXl4PISL5SLoye9Ttec5DqIi2bRja9OQwJJzunkQip+lD2ywMtBdC2ENik2+VS+BPxtqbqgwOgvlwCg+slCHiFji2sfi1A+awthgSbItB7D0g6lkACyoE3QO+hx12WPOs59jH9A0z90Gw0497ITY0xfWnECgECoEpRaCI+pROTJlVCBQCC4MAQhayZnuK4/zsY0YQnfxhm4t9zzma0d5nxBvRQ8qVOy3EaSS2zfCAe7gUibTtArn2ICoyjaTrC7EkF4JIBjlMkI6HV13kkEx1vaw2IZdpP+0x7FwwYbsrebYbb7auIN3xosPVm0o///nPD1/+8pfbQ7d+6TAn2iPvMPIwaBYvyjxo6mQep/JY5OhPEMcGmMaO1E87jmVfIVAIFAJF1OseKAQKgWWLAJLmQgyRM97ZQw45pBFq2114ZBFr+9GduMLL7mhFD5Ly7CLcvL7OWHeiCF28tx5I5IFX5iFQD5ciksi5c9T1gxjaEoOE2rcub8uGoxelkXvyAoKq3MKBTE8k6c3Vl0/rpLEVTgLcBWUItEWJPfqINu+4bSli44IT3GD1h3/4h827bg+6rUheREWHhZCHS53oku1GFkwe3qVfexj65cMCDM76g68HgV36in3SsbEZWn8KgUKgEJgyBIqoT9mElDmFQCGwcAggYrlotX/c6SvINgKOKCLLYsTOS4f22GOP9oIipO93fud3GmlHJpH57D8n6zQR+6F5hrVH/pB3p7l4cZF+Hb1oq0befoqc/+mf/mlrQ44eRPFTn/rUcNxxxzWS7oFJuhBTdS5p+pZCYGdsjr3sR5rhe8YZZzQ8EGvjtFDiJYevuYAr3P7gD/5gOOqooxpJJ0OHLTIwPPzww9uDuBY35lG9cv16sNTc+fWDnlNPPbX16xeMnBSTe2KpYBocKy4ECoGVh0AR9ZU35zXiQmBFIYC8CYihNI83gseDi/ylDpFzIYuII/KH8CHZkUU2s5ed5xepDKmmh37tQyzttdZv2vACO6pRG7rIihFPJBJx1GdspjM2NkOX2J8QYeMxTrgg0HnZkHpYCLztcPeLAlwsZCyMkHMyZGGReZK24MrWIeVkeN3F9OjTwgdhl85pPNqSqVAIFAKFwLQjUER92meo7CsECoG1RgAhCylG1ASkEWELQVRGTrmyXPLIH/IYUicOyVOOgCtLvT7SZ/pK/2mHiPPAh7xqy54sDpQLypFQ7SPbKqb8Tz/+4JLYWJB1W1CMyTWWhw354AGvYKfcRY+ykHOLIeX09XOijJxy6dwDgTB6k6+4ECgECoFpQ6CI+rTNSNlTCBQCC4ZAyBuFIWrIL8LmCglG2IQQOrJpI1YfEp5ysq7UJ6afPKIpkAmxlE/ffbkyBFZZbBH37ZqyJfCnx5y58EiZ8UkHX2NUn18g+jpt5cmoF4JHsJMPdulLrEzQlo5x++glJ12hECgECoFpRaCI+rTOTNlVCBQCC4JAyGBIGZKXEGJMRkDalIVsS4f09SQx5C5EkJz6tEsb9crVp41+Youyvj7tlbvIpQ910Rv7pzlmP9uNXZB2GYegPBdZQWyBQw4uxtu3j046pNX1+PWyyiPflP/qDxnl6a+vq3QhUAgUAtOGQBH1aZuRsqcQKATWCIGQLuQuIenU9QROma0SIcu9rHSfjz5tXKlTLp1y+aTTV4hiysdttQkZTXrcRvl8Q69/vm0WSy7joN/4BWVshE9sTVnskE+9dpHr4+ApJquNEJn0Fzn1KcvckE9Z2sWGimdGoDCbGZuqKQQWC4Ei6ouFbOktBAqB9YIA8oCMId8uxMvDnwLv7JjIKQ95CylURs8k0qY8dalPWeuk8xb3eelev7z22iawoyeP4/rIiSPrQUvjM1YhY6an1923Haf1k7GoG49nLD/Oj9uqn6Rz3E4+NoqNSbuMRVq5uMcl+nt9wSMY979GpC094z6VpZ9eX6XnRgCucPccge1EPl/uxcxF5nZuTSVRCBQC80WgiPp8kSq5QqAQmDoEEAQkz1naV111VXvVvLKeoCW9LsaHPPYEL2XrondN2+ofWXIkpBf8OB7ya1/72mrCy6b1QZZ6HNZ0DORnm5PU9ePo02mvDBYhjyHq8pF3LySkLPrH5clXPDMCwRDWcEbWvY/AC8OcXT/GdmZNVVMIFALzRaCI+nyRKrlCoBCYWgScwb1q1arm6UMWePqQiYXw9NHnQlJCVAJEiMm4PPULGesjYzKuZ599ti1M7rjjjmYfzybiNJst47FEdry4Sfkk+8c6+nxIcspma69P/eSKrHJhkg0pS5w2+kvo9fXjSn0f97J9eaUnI5A5c5+5F4VXX311+MlPflIkfTJkVVoIrDMCRdTXGcJSUAgUAhsKAcTQXnNnmnubqCt7zxEJBC75dbWxJ3Uhk/SPSeO69jNT+5BfY/bWVIsTb+0855xzmnfTLwsWKLOFntCO5TKWucYTHZGLXcFHHJlxH8mnPjoSKw+2xpmgPDJiFzlX6vpFQtqJ01fKej2T6iNX8TsRgKUL1sGdN91Z947K7Ofsna2rpBAoBNYGgSLqa4NatSkECoGpQQBZ83IbL9LxMiHevhCKkLJ1MTY6xPQKIZPSqV+XPubbVr/6403nSfcWziOPPLItRpwfPlfobc1Y0ma2usiIyc0lO9bdt0+615GyzJt8SF+vK23Evaz8uKzXmbQ4sinr9aes4tkRyP1vjrxd94YbbmgNUj5766otBAqBNUGgiPqaoFWyhUAhMFUIIAaIFnLuIUuXdB/GxKyvW5N0CF3ihdI7XxuMNdsN/Eogz4OOLCHpedHPbPrY7mL7OMx3XJFL+15XX9eXR3Yh476vPq2P8dyM63s7FtvOvq+lnoZjrozFPZhfclJXmAadiguBdUfgN/+jrbu+0lAIFAKFwHpDAHG15UOMHMQLGwNCGGYjapGdKZ6kQ9mk8pl0LER5xmYsxitvUYK0W6CwZ65xxuNJbjyGudr2Y4ieYJC4l5lNXy8fuZTJu+RTNklv2qljT9rAI2XRET1pI458r7vScyMQLEm6B4N3PodzayiJQqAQWBMEiqivCVolWwgUAlOFAJKALIR4hbAxEqFQ51qIEIKSWJ/pT1kIy0L0NZMO/YQQ8WIi7PrN+GPbTO0jy25XH9YEK7L60i8bxIKyNdGTNuLgSR/bLEKirx/XpLQy7cXa2jNNj33Txqw8V/ok15cprzA7AjB2wVYIfsE+WM+upWoLgUJgTRAoor4maJVsIVAITBUCIYU9QZAWkIiFCEiIkFiabvnXX3+9nXhhj/xWW221EN3NqkO/2WrgYVLHNCbMd7xvvPFGexj1lVdeWX3e/Kabbjpst912bb9x8IvecWzcwQIhfu6559peecT3Ax/4QHuwd/PNN3/HFiR60q7XqQzxc3KIyykizunecssth1122aW16bczRUfijDsxXH784x83m+yfZhNdm2222eotGvonnza9PZWeGYHglXsk+XwOk59ZQ9UUAoXAmiJQRH1NESv5QqAQmCoEeu8uoiA/JnHrYjBdLrrFSCUiiSTffffdwz333DPsv//+w+mnn74u3cy7LTsQJePkMV4TcoRYs/nqq69uJ8YYg7Ldd999OOuss4ajjjqqkfXZdAYP7RyJefnllw833nhjw8Vi5aSTTmoX4p+56PGTVu6CpV8InGJzxRVXNJucZEM3kv5Xf/VXw7bbbttwTzsLgrSXju6kX3zxxTa+6667rulG0o877rjhQx/60LDjjjs2nLXPfM421nlPygoThFnwg3s87CsMhhpuIbBeECiivl5grk4KgUJgqSIQQoKMSCORDz744HDTTTc1gorsOh5yfQdkM57N+fbtKL0LL7xwePnll4c999yzkWAvi/LypMsuu6z9KnDQQQfNqjcE+5FHHhnOP//84bHHHmsLFV7ve++9txFu3muebB5tRBp2Y3tDvNU98MADw1e/+tVhp512GvbZZ5+BR/6aa64Z/v3f/33467/+64HH3+LIwkS7kHXzgeiL6fdrwc033zzccsstw9Zbb92uxx9/vL0My68eG2+88bDFFls0+dikbYV1Q8CcVCgECoHFQaCI+uLgWloLgUJgmSCAyIUIipHEN998c+C5RQIRRS8bWgqBvTzWPOgnn3xyi5FkpPvJJ59s207mGkc8qLfddttw6623Nk81bzyifu211zaCfd9997XjMhF1BDoY0o0ghySrs9WFvPhv/uZvVm93QcrPO++8thg65ZRT2gOz6Vtf0vRarIiRRWPj3edF//SnP93elmlsl1xyycBe40bYbR/SRv8VCoFCoBCYZgTqW2qaZ6dsKwQKgQ2OQLyFIZxOWOGNPv744wfe55DRDW7oPAzgleZNtz8dWUZY42k2rmypmU0Vgquts9z9urD33ns3T7itKkccccSw/fbbDw899FDztGcBEyLdYwlP9fa433///a3vQw89tO2Vt4XmkEMOaWbYpkMu8rFRPlcIPFJuMaK9LTMuc7Xrrru27TX66hcJs42z6gqBQqAQmAYEyqM+DbNQNhQChcCSQQC5RQR33nnnFj/xxBPNO7sUBnDMMce0xYV95R64/OQnP9k84V6cZPuOLSZzhRBdhNlWE2QdURZ4wd///ve3cr86kA05T6xd0gi8YAGRXykQfXrg61cL+NJPhiddeyHkP30rpwOpjx3KtLEIsUAxTnoqFAKFQCGwVBAoj/pSmamysxAoBDYIAiGTSCdSKI8AipXZ+hKyuEEMXINObQn5oz/6o/bgqK0u//qv/zr8y7/8SxvDGWecMey2225zLjp4sY3fHvSnn366bSvhxUbYedntU3d6S+TEwTCmJk8Pj75944j097///Ra/9tprbQsLko50C2QtkjIPcJfu+0HyydjOY+89Uv7SSy+1B2jZ6HkCbaIj9lRcCBQChcC0IlAe9WmdmbKrECgEpgYBxBIh5Al2JR/CHg/x1Bg8gyGOLrSP3BaQs88+ux1ZaO+2/eE87LabIM7GNVOAA6Jr2w+PvH3hf/u3f9sIMiJsAWDLSU6UoUubHj+6YabOQ5+2vHgw1cLBvnQ20GOLjtNj2G2LUXAXh6TTJS04fefAAw8cvvOd77TtNx5K5WVH+O1Ptw2Gxz/jy1y2xvWnECgECoEpRKCI+hROSplUCBQC04MAMhePOYLoUhaiiYAuleDhzxtuuKFtc0HUnbJy4okntpNa7BOXt/3FqS2zBUQXKSZrPzoiLPCw23qCICPWvNtCT4jhJyTmmf/gBz84/N3f/d3Ak84Drn8ednrVv+9971uthydd/y4e8ywCzJFfDD7xiU+0B1Lp0Y49jqS0/YW9tsKk78RNef0pBAqBQmAKESiiPoWTUiYVAoXA9CIwJu2IIsKX8niOk1c3LWTeuecI7L777ttIuXPFebR503nG7Qmfzx5u40GgbZWxX//www9v43fiim0nOfoRKe7xgEXIMfIuIPO85qeddloj9Mg6GzxEakuMs9152KNHHD3jNPK+xx57NI++/fPmIA+2OprRAoBNQvqPPa2w/hQChUAhMGUILB1X0JQBV+YUAoXAykAAkUP4bK8IuUMkbcfgrVXOy4sYurINIwQwbacBLR5nwV5ypNy2EPvJpY0hJ7/MZWuwQHptJUGCEWwkHfG2/cTDqYizAAukWoBhLnn4qIv3HabOQr/yyivbiTIHHHDAapJOT49r9GZe9Jc0fbzybLK1hz0WF33fzaD6UwgUAoXAFCNQHvUpnpwyrRAoBDY8Akh5iClrkFveZ9tIbM1AAr2cB9n0sh57t3mAEUJEMsRxw49kGPbaa6/2dk4vKXK2uAc/LTjkecfVs30+wcOjXpRkKw2MXn/99bb15dhjj21ecN5rJFyI5zt6e2xga7HAG08Xe+BK/0c+8pG2nSXkXEy+XwCkjm6LDVt4vIzK4sMpL+bHCTKHHXZY25ITW/p2saviQqAQKASmDYEi6tM2I2VPIVAITBUCCF1P6pBSxBKRtGUDseVZzpYNxofYZ+sHcjgNwakop556antz5wsvvNA8zmw0Dg+S2rISz/Zs9sLDmPyCYNsMLHjrkeGTTjqpkX564i3v8Que/QKGF/2pp55qCwceelte7Fs/+uijV3vjg+GYaI8XAx5idZ46b7pfCGzzsXiwp55Nfb/G2Ns225irrhAoBAqBDYFAEfUNgXr1WQgUAksGAcQQuQshdFygl/sglNn6oh5hR3hDzkMIxb0XeEMO3NYP5Nc2EN5mvw4gswg8rzMveAjxbHYit0hv3nBqfIi68Xsg1UOcZOL5pit49Gky+oOdLS6wk2aHhYOHUukgpw+yycc+86I+sX33J5xwQvPMG6+8XwtyagzZhD6dsooLgUKgEJgmBIqoT9NslC2FQCEwdQggmAhdLkR9hx12aGRXXS71yCuyGQIY8jgtg2Ibb7VFhm0utoogv4i1cbF/PsGYtUPwEWvjpJMOxD9Y0UU2OGgjrSxBGR083t4gKtCFZAdLbYTE2tCRfsTqkHlHQ2orrz1dxofgqw/hzxw1xfWnECgECoEpRaCI+pROTJlVCBQC04FAyCBrQlARUuRP3oUU9sQv6chPx0h+aQXy6uFPNob4sjPeb+nYP8lubdIOKUf8hXi6tXXRI0S2L4v+yCDePN7ssniAbdo1Jb/a565OG/JC2idWpm3mJrakP3H0hrBHV/qpuBAoBAqBaUKgiPo0zUbZUggUAlOHAHIXIhjCx0hlyYsjl5hMyO+0DCo2I6cIa29r8srmCr1M7/Wmf0x8e9mQ5F6m71d5LjZIh1CTi/6U0d23z2JB24w19crIZ07UVygECoFCYNoRKKI+7TNU9hUChcC8EFgs4oXchfRJJx+j5EM8x/XyCxnYgXgKdCOsSSuPHa1whj+xKbYSo7cf4wxNW3HfXpuE6Evclycd+ehInt1JI/5CZJJWT87VYzCWS//RRz4yidX1pD72VTw7AsGUVNIwDcbBd3YtVVsIFAJrgkAR9TVBq2QLgUJgqhDoyUJvGMKQur58bdP05ep1hJgk7usWI21M/bgQJEH/8yHqvZ1Ji6M3ZbPZTiZyiWPDpLjXFXtTNpOuXk/axBPet4mcsuASm8Zx+uzb9GWVnhuBMcZpkUVP6lNecSFQCKw7AkXU1x3D0lAIFAIbCAHEAEF1hrfj/ZyhHYIWk8b5lC/F2Fhd3i7qcua4F/pk+0lI7VIcW9k8/Qi493zm3GeJHc+ZF0qlfjl95qZ/VsrC5Y5AEfXlPsM1vkJgGSOAECAHzjVHGBzn54HDnij06aUORYiQhYm3iyJId999d9sCE6/mUh9j2T+9CLj/BETdtiunBD3zzDODM/md2OOztpw+b9M7E2XZSkKgiPpKmu0aayGwDBFAGpzy4fQRxwUKyAKPn2u5hIwHIffWTUcaOnrQueUw8CImcYVCYLEQcA/6bLkHEXWx+85pPbVQXCzUS+9KR6CI+kq/A2r8hcASRwBxcG62l+94MybCEFK7nLx7GZPp4k2//vrrG2E/+OCDG2H38iXjXU5jXuK35rIz3z0oWBCGtDuq1Muu8hDwsht0DagQ2MAIFFHfwBNQ3RcChVkDoCIAACAASURBVMC6IeDneOQUYchLcvqf6NdN+3S15sU0NuM0XnledR5NHvYKhcD6QCCE3efO/Ye4uy9dIfDrw47qoxBYCQgUUV8Js1xjLASWKQIhBQiDdAgE4rDcPMsZq18MBPl4Nvv8Mp3qGtYUIeCzlcXwcv7MTRHkZcoKRqCI+gqe/Bp6IbAcEEBWJ+2PDYFYLMJOf/qAY/pJvBjY0m28POn65s2U7vtf034zhrWxe9w2+bWxpyd+vS3SfT7j09dM5b0d5CMLu3FI3aTysZ7IzGRT6ifFdPX60u+a6Eqbsa70N2l8qZsU9/aoT34mPanvbZb2+ZupzaR+q6wQKATmj0AR9fljVZKFQCEwpQggC4hCrhAK5qpbiJCf9cVvvvlmu5wwIyAq73nPexpxtiUlpJM9bHEtJJExpowx6fno16bHw772N954Y/UWGrbHYz8bZuk7mGgDC7qUebg3usZ90qssF3veeuutdoKNMu2dJpJ2tvnA1h5oixLjDL6xMbLyP/3pT9txnalLf2zK1ih9Bje6pOkVRz7YiOlPubEam61G7EybJjDhj7awcVKP4zTTr3LtN9lkk4bXXHrYSY+HN+EsFtgTzJx6lHEEk/RHNuNQpo08TOmKbu1tpTLGcZteF7n0Eb2tQf0pBAqBBUWgiPqCwlnKCoFCYH0igCwIMxGFucjPfGyl2xVC9/zzzw933XXX8MQTTzSCo44dO+64Y3uYdeedd15t07p6u3v7jCXj0Z8LuQpRk2dLZPq2SWcM8mSfe+654dZbb20keb/99hsOOOCARmYjPynWLlf0IbOPP/54w8WYDz300AEOyDG7EtIueTGSCMsrrriipckj5XQjsUcddVR7UJis8aoPFvpKOvWOq7zxxhtbOYIv0LfbbrsNBx100LDVVls1HbGLTXT0ttELmzvuuKOdz6+ePFsR2D322GPYf//9h2222Wa1Pa2jCX/oevrpp4cf/ehHg3vHryD6Us6uD3/4w8Muu+wy5wJJG8eQ3nfffcNDDz3UyLq5d8HFiUennHLKsOmmmzYryCf0Y8ucKdOOTd5B8MorrzT9xucBZXgJxp42+pLvAz3GIlY3ru9lK10IFAJrjkAR9TXHrFoUAoXACkMgJARZc+IK0oUs8dCqc1zidttt17ysYp5SAYERkm+ZBfgTMhS7ojLlyc8Ua8fzbMHxjW98o7086Zxzzmnkmjd1Nj0ZEyxcGf8111wzfOc732neWEdlwiFe2Zns0B5ZRNTZgcTuvffeTVw5Ur3nnns2YqwfIWPWli1sjb3a3Hnnnc2ObbfdttmAXFowmAMnAzmhhI7oC/lERgW66M08r1q1qhFycx2iThdyvfXWW7c2M/3Rh0UMHd/85jdbeyTfOOlS/8EPfnCm5qvL2eZ67bXXhmuvvbYtrnjPLWToYK/5PO6444bNNtustYOPoD74RKGy4A6vJ598stnD6w+rHXbYYfW56DPpiK6KC4FCYHERKKK+uPiW9kKgEFjiCIQIIjcuhG2fffZpZAZRs23jlltuaS9cuvfee5s3Url2IbJIVojT+oajJ2qxwRYM3uKbb765kTRk0jjIzhWMK6RWzCNLz+23395efoMII46TCHAIo36CCTny9PDkfvzjH291yniceYrJkEeQtXUhmkJ0SpMxNuOk6/DDD2+LBXnEFomVJpe2/XiCj371b4uTxQIC7BcCsi56eK7J9/03paM/9CDYPPRHHHHEcMYZZzRbEHV2WFDMpSPzQp4uOo899ti2WIgNMLLIUictaNfrlo88L7oFpxeFOYvfwoMsjC2y6JAfYxVbRsOsbCFQCCwSAkXUFwnYUlsIFALLAwHEJJcRITVnn312K0NqXnrppUZybf3gGebZRO6QnFzITkjg+kClJ1Ns6IP9zffcc0/baiLNy4xEsi8krpcfp0Pg9MEDy8Pr4t1Fjm3PQHRdY6JHV2xLnVgZjJDpo48+uuGJiFsUCZHt7bO4CCGNDDkyCGvO1ZdmS9828mmvr9QjuuyJLjZZmO27776/oSfji2wzdMIf9Ui5PmwnOeaYY5oefbt/bM/R92whdoY00+k+tMWId145Gd5waVfslyYvKJO2AHnggQeG+++/vy04bHnKm0XpMJdsItvriR2z2Vp1hUAhsLAIFFFfWDxLWyFQCCxDBJAVAelBrGzpQGJcyBZvNCLGy4rkIDQhTNJpvz6giV366gmgcjYiaFdeeWUja0ixxcV1113X7O1J6ly28lzzonvxknHz8N52221t6wk9Ccaeiw0hjj0xVoZ4exU9T7/90ki6F1hl+0yPIXm4K+ttpp9ettmaxLvv1w2x7TghxUi2oG1vm/ZC7DSvtjUZlwUYXfalm2OBHT3GrXDCH/qQY1tg6DIPPPS2wcynPZV0uNhrgeTXG+OxEGFXPPPut8hplzHqx6XOrxf28ovNnYWay3hsNbIogW+wna+NE4ZeRYVAIbCOCBRRX0cAq3khUAgsbwRCEJEYIWQH4UFknnnmmeGRRx5pxMYDmUgcWe1CcBKvD6TYJcRuaWVsss3h8ssvbw9+2hbCXkSUxxeRREyNKUR2kr30kEWov/3tb7e2Z555ZiN8ypFQehDvkOnoCSbBMuUIJ8/1q6++Opx//vntVwpEnb4TTjih6WEjfT0RNS55IaQScSVnQWJsPMTINU92iH/61z42Sff6LBC0tX/7pptuag9xsske+jzgqn6uYO6dEONXFvhffPHF7VcH4z333HPbdhj1/XyNdcYuOGWx4VeRRx99tD1Uutdeew2f/vSn2/aV/HoAD+PUf+6/jNf2GVtfXPQJFiJ+HXr44YebvIdltdNGmM2+JlB/CoFCYFEQKKK+KLCW0kKgEFhuCIQgIi4uJMgDh/anI+uIjS0ECE3IbshNCNL6wCR9Jtan/tnkhBfec0QWiUW2nSLCs/rYY481Isk7y8s6U6CLx/uqq65q3nTbLxA+xBjJU4fcwsb2jJxyEgyQP7bJC2xxYg7Sihy7LHZuuOGG4b//+7/bswAWFAnG0euQp89Fl5Ndsv9bzLN+9dVXNy+7hyT7rSIh+T1W5pVtiLS96TzM5Hj7YWVsyG0eHo5dk2J6EWfbSj7xiU80u5Byv2LYH24c9KSPSTpSxia283aL2Ydcu//OO++8thDQh/3z+iVvLGzP+JS5YOay0PAMAJ1kedktAIzPLxDmT1AXHbGn4kKgEFg/CBRRXz84Vy+FQCGwhBFAboSQH/HLL7/cjgH0IKWtFY7GQ8h6EklOPu3XBwSzESq2IGC83og0oodk26uOYNv+YNvIbESdfp5u5A3BRo5zXCDCTw9SK+bJRga1CQaJgyebEOhPfvKTzfOsnF3kvvWtb7XtNXBFcMmyPeSTXmRcuQsptmDyYCQiyqtve44TVx588MFGkGMzee3JJa1Pl3K2n3jiia2eTcZmrBY7POO8/+ad7GxBG9tcLET0xcZ4s20b8ryDvetZNMyki11IuF8Y4G9BY3y86f/4j/84XHDBBcOHPvShNndkjUkY26dOUG+MFlq2QCHnxmMhgvwfeeSRze7oIB+smoL6UwgUAusFgSLq6wXm6qQQKASWMgLIDWIqiG0R4Jl2JCHvppM8EB7kCTEKUUp6TJbWNxZIFoJo6wdvNYIn7xKQTmQSIbZ1ZLZgLLy5zv8+5JBD2ljpocOWCmPnpeWZR/4y9sS9bnaRR8KRa3rgazFha85XvvKVtiBCzpWTpcclLdAR3dLmwyVoZ8HAa+1hX4sQZJNdCdEVvfqRjlc5BJpOnm+/HFjY2N4z38AuJDuYI+/GaxFhLuYKxurSHrnO2LNoMR9+1aFLXRYyaUd/xicORuaMbe4J8w4ndlpIWAwI6oVeVyuoP4VAIbBeECiivl5grk4KgUJgqSKAoCA3ApKH+NmW8YMf/KB5c3ldnQqCNCGqyDovctqJpyEgXMghAs2mEFIeVKd/eBgxW0Pmstdebdt87NeGCXwQRVtDnPpCjz3ZsMj4gyHdfVo94msrDk8+kulhyXj8kVCkOd5cZDX29ySSTu3MDxlkH9mkRxk9CCm5vv9+AZC02K8LiC8vs/nk5fcrinlGao1NYEuvr8dOHUKfRQLPubbsca+wB2mfK9AfnOALD4sbdsLNLxgIfI83efikrT6kXeYPIffLAFJuXGSNUWzM9NMh6Ee7LFrmsrfqC4FCYOEQKKK+cFiWpkKgEFiGCCArIT2Im9M2Lr300naCBy+0t07aA43EIIMILOIekgOSaSE4CF6IYUgpEpqgbj62kolXNm2RPESRjhDEEEMywUOZdPpHwO1t97Ik21ZgaJvKJZdc0rbWOGZRf8h39GVxQG/K6EQ8HRWpzIkqiLq3lNq2YnuHRUr0hHymvTg28rzbq+0hYb8OWEDYw583nvrlQRl5Y50t2JrDLr++HHjggW1Mng1w+gtyjazPpSO2udec2EOeDe5Hi0YLHeNjE1mBbRnb2D5yFlkeRvULAVJuYQV3CxsLCjJwhj1drqTH+ipfCBQCi4dAEfXFw7Y0FwKFwDJBIEQJuUPiXAiYLTDe7Ig4uex/RjSRILLZmoDgTEtAuISMiXeVN108F2FMO3LRI6YLQbd1Ir8qIHkw6Mfek2PtyAgINa8+zzPSyGtM32c/+9lGuMnQo70Q28WuBHPCE+5hTUQb/kishyUdH2mciHr0pF10ZPzybGMPPcqzb952H4Q7Hu20ia5JMUJtfEgwAsyDzeN/+umntwc256ODzXBBro0R2WcjXR56Pemkk1bPYcYjzjzFLnmLLA/ossf4PNiqjB0Wn/anu5f79tEZPRUXAoXA+kGgiPr6wbl6KQQKgSWMQMgO8sjri0DavoDYhMBI29aA6ChzIZdihApBnIYQe41J2njYzaPKu7smgY6QXgTUg45+UXBaCO89/erFrp6QSgdXmH3uc59ri5/IqXeCCy+4tPIQe3nkV/uewNNj7zwiG1n1FhA888aprbropCOyyuT9ygAX5BURVm/+LGaMDYmNZ342vNjsVwa6vvCFLzRRfVhQwNoCAu7KZgtsImN8H/3oR5tNFiHKXDm5RV/6dE0K9LgEY/AAtF9/slcdPuxSJw5OsS9zOUl3lRUChcDiIDAd/zkWZ2yltRAoBAqBdUYgpAfBQc7sv84DfanrO0HmUx6iHjLby22INLtCtqRdiGc8zYjeXKEne9qHxCG1HrZEIOEUHEIM6SWfvFhbZfrnXUYM5V3SdLgSyLNfDFsh2GrDS+2BWTbQr0xs0RBi3fevPvbTJU8f3cgqu+T7PulJ33RFPjaOY/Yj2HBO3xYZsI5d4zbjPCy0ZY+95doHO/1bWNAlkEs/Gb+4r5PXxjML7KJDGZ3B1hhTrm3SGXtTWH8KgUJg0REoor7oEFcHhUAhsJQRCMkRIyshaiE2iEuIUWLjDQGM3DRgwL6MJ7aGLIb4zWWn9tpGV8apHVIKn+judcFOSP99nXbsQEgFOpOWl4azC0mlS7rXqU/tEGCXOn3lSn/KYzO90q5+TNKZ58xv6tNWfqw7ffQxeWMTZxzSbBTHnkm4RI86smzRLjgrz8KILJsSq0s+evSVMrroTCCfNuRil3rlvWzaVFwIFAKLj0AR9cXHuHooBAqBRUQAiRBCQBaxq9WERV89sRn3nboQHqRvMYJ+Y8t89MdO9rEt2Innq6eXS/v0nbw4OiPf15HvbVHHHmUIYdpIj+1UFt1jnbFDnDq6oi+6+j7IRTbtkxdrG319eZ9Ou9lievQr9CQ5emZrSyZydERPdKVtLycd28XBl6y8+ujJoijyKU+fvf60T1nFhUAhsLgILM5/j8W1ubQXAoVAIbBBEEBgkJkQnZChEJq+nIEpXyhjoz/6kC8ka7799HIhY2trZ9+eXdHT9xE7lY3Lg2XKxcr6cumQ68hZ9EinPP2mr8SRlw9u6SN1CHPSYz0p78cW3ZFNXV8+KW0caUMvD3v0J57Uri+LnNg17jv1fZv0mbiXiR517IvOvnwmXcqD6Vim8oVAIbCwCBRRX1g8S1shUAisRwSQNVcfEIhcs5GOvs180yFH9ArJp/24PP2P5SK/JnHG1BNZ+qO7J67z0Rtbx7LRNy4f5yfJTSpLPzPV9eU9odWfuknt+/LIje3r89ER/X2fM6XTPm2TTzxXu8iJex1pl7iXmymt/SQdve659GXsk/pIXd/HWC51fT9J93XKkh/rqHwhUAisOQJF1Nccs2pRCBQCU4QAUoCk2qv75ptvrt4jPSbwU2TyWptirC4v9jFWpIhH3RGEFQqB9YHAmIh7oZN7ULmrQiFQCCwsAkXUFxbP0lYIFALrEQGeQOQAaXUknxfLCMoQdXG8hevRrEXrKp5KL75xBrZxOzNcSN2idV6KVzQCPkv5XGXLkM+W+9DZ+dmCVffhir5NavCLgEAR9UUAtVQWAoXA+kMAIfcyGkTdy2AQBmUupGE5EIeMI2PiUXf2NW+mxYlfE5bDONffXVM9rS0C7sEQdc8LIOrux9yba6u32hUChcBkBIqoT8alSguBQmCJIICgOhPaC3e8HEc+3j9DWC4E1jhChryhcsstt2xvSDVmYTn9crBEbr0VaWb/eZK27coZ+iHvKxKUGnQhsIgIFFFfRHBLdSFQCCwuAgg5rx6Svuuuu7Y3WeYoRHVCTywW15rF1d6Px3YXL17ydlRvAs0pIstlrIuLZGlfKASycPSiKZ+73KMLpb/0FAKFwDAUUa+7oBAoBJYsAogBsiD2EhiePYQhD7cZ2HLxNPfj9AuCcdryknGr35BjNQe1UFiyH6V5Gx4yzoMunRc3pXzeikqwECgE5oVAEfV5wVRChUAhMI0IIKYhh4hCyELK+vp1tZ/u6KUrfUmnvC9Lecois7Z29O2l481MvKZbDyaNp+9jNjszpklj7HWM+5hNZ9UtDQTMaS4WS7sHhX7ul8ZoyspCYPoRKKI+/XNUFhYChcAsCCAKQk8SpHPN0nTeVYiIfvo+QlD6xYCyXk5dSAwivS6h77vXkz7mqz82ioXole/H0vcxThuTK/La+hVD3pWgnH5l0smnz8hVvLQQMH8u8ylkPpNfWqMpawuB6UagiPp0z09ZVwgUAhsYgTFJR0g9QOeSRlKQZNtRNtpoo0ZKlStLvJhD6AnTfPph089+9rN2Us7Pf/7zZi/bbRsSz0X4kTFbbkLK4ODUHThpa7+87TiwiC6y7Iytyc/H3pIpBAqBQmAlI1BEfSXPfo29ECgE5kSgJ5gI6qpVq4YrrrhiuPbaa4cnn3yykVIPdB5zzDHDUUcdNey1116rPYzIqzb28U5DQJA9iHrppZcOV1999fDUU081Ms3+s846a/jgBz84eDBwtkBHFiGOhvzWt77V9CH9Huo9/PDDhxNPPLFhsckmmzRVPOra9N722fqoukKgECgECoFfIlBEve6EQqAQKARmQQAxFRB2L3a54447GlF/+eWXh4MPPriRz0ceeaQR8t12223Yc889WxmSrk1OZJmli/VWxZ777rtvuPDCC5ttZ5xxRiPut99++7DxxhsP++yzz5xEnY6333578NKlr3/968M3vvGNtjjZd999h8cee2y48847h80333zYf//9h6222qp53vOrBCylhXjb19vgq6NCoBAoBJYgAkXUl+CklcmFQCGw/hBATAUk8wMf+MBw2mmnDUcccUQj5raLePHQ5ZdfPtx0002NxB922GHNg46QumwDmZbgOEd2sun0009vY7H44BV/5plnhgcffHDYaaed2jaYmWz2CwFMvBX18ccfb4T8z//8z9txkddff/3wpS99abjnnnuGU045Zdh5551/w4uuXXnVZ0K2yguBQqAQeCcCv37q5511VVIIFAKFwIpHALkMwXQkou0du+yyy8B7vv322w/bbbdde/mQvd9IO0JPnsc4R0XaFjINgceb999Lkg488MBhxx13bGfPH3rooc1Lrs7LlGYLxmV8999//3Dbbbc1Ug8Pumx7OfLII4cXX3xxeOCBBxoevTed3uA5Wx9VVwgUAoVAIfBLBMqjXndCIVAIFAJzIIBoI5wh38Sfe+654aGHHmqE1HYYRPXkk09uD2TyGpMXQvLn6GK9VNtTz3O+3377te0pefDTQ6QIOiIvtviYKRib64UXXhhs/7EPPbj4hWGzzTZrY/eAqcVLxi8OJnSXZ30mhKu8ECgECoFfI1BE/ddYVKoQKAQKgXcggFwimbzj4uxZR3q/9rWvDTfeeGPzUCPp9mSHkEY2BP8dijdAgb3l9qLbQ54X1bDPZVwWJLa2zBUQ8+jyywLCHz3a0mFrTIg6LIJHfnGYq4+qLwQKgUKgEKg3k9Y9UAgUAoXAnAjw/iKafbCX+yMf+UjzINur7QQVJ6r0p76QR2CR/GkIxmB/OpKObCPNIc7sRKzFcwV4aMeD7pSY6Erb6KVHWrm+yY1xnKuvqi8ECoFCYCUjUHvUV/Ls19gLgUJgTgSQ0mzTCOlEPLfccsvh+OOPHz796U8Pxx13XDub3EOUHs5MQEq1DYFN+YaKEWVnqL/++uvNI96TZ3W2wMz18KuxuJB9emyX4YkPTjCyMPHgLU+7cv241FUoBAqBQqAQmD8CRdTnj1VJFgKFwApHICQ1ZNR+bFs/XMqeffbZ9iIkpFToifA0QGfLCy+4lxSFrCPZtqkg3rbuqJ8tGBPPu4UKMm7MtrrARqzO9hq66FSuTbCbTXfVFQKFQCFQCPwmAtPxe+xv2lS5QqAQKASmCgEkU+CNdqLJW2+91Qgtj7EjD734B/FF2GfyoIe8b8iB7brrru3EGl7we++9t5FpvwDcddddbaFhOw/yPVuAhUXJ7rvv3s5dR9Tvvvvu9oCqh2thYQHjgVRe+hD18qbPhmrVFQKFQCEwGYEi6pNxqdJCoBAoBFYjgHzzFDvJBCl1NCHivdFGG7UjCB999NF2bKMjDycR3Wkg6QazzTbbDMcee2yz2dGKFhkWH06w8YIiF2/4bMFY4GFR4kz573//++0FSvQ9//zzbRGjD0dX5gFc8oK2CPu04DHbOKuuECgECoFpQKCI+jTMQtlQCBQCU4tAPMgMtJXDHm7k1sUbzbvuXHJHHh5yyCFtn3eIaOJp8SYjzs45Z/OqVavarwNsPOigg5rt3qo61x51OBiPBckxxxzTfkl4+OGHmy742LePqMOERz3yIevJB5smUH8KgUKgECgEJiJQRH0iLFVYCBQChcCvEUBMEU3kFCG35cW+7mzt4Fm3bYQXWSDvChmVDmn9tdYNk2IjMm0bjL3qiDlS7Rx4W1Zi80zWpR4e2px00kkDgi94GJV+l7RxC8EDBilrFfWnECgECoFCYFYEiqjPCk9VFgKFwEpHADF1IZjIqb3XCK2tMKlTzpvMY01Oefa1TwtBN4+xc4cddmjHKrKRfci6xcd8bDU2erQ15j322GOgL+X0zOaVJ1ehECgECoFCYH4IFFGfH04lVQgUAlOIQEixOOmYmTKkcl0DckmfgIi6+pD6kFB9Rl5Zyvs2a5Pux5hxpczCYS6iHVsQ6fH+8TWxpx+fU2J4zxMQ+PTTj7tPR7bipYWAuXW/9fNvBMrUVSgECoGFR6CI+sJjWhoLgUJgPSEQ0oAkhESIQwrVu5JfW7O0d03S1Zf3/YRI92Vr2792+k5IOuRIX94UKp5Pf7GNvvnIp9/E2tARPKIv+ehdG93po+LpQiD3HKukk8+9kPLpsrqsKQSWPgJF1Jf+HNYICoEVi0AIQ0h6D4S6EMWQir5+bdLR17ftdffpyEwqS93axPS54kFnk/HHm76m/a2pfGzWb/DodaSMXF8+KR9dFS8NBMytOXX1C2LWz3eRuDRGWlYWAtODQBH16ZmLsqQQKATWEIGeOHjZTt6QicQiEyGvPXlcwy6mRjzec1tWPMjq5BZ7xMXGaoy5psboMmTZIeBe8/kKMXf/JW+wuReX3cBrQIXABkKgiPoGAr66LQQKgYVBAIF1esmDDz44/OhHP2pEIcQBmZBeTkTdfvAnn3yyHa/oXPfrrruuPbxpoVJEfWHuqdIyGYEsfLMglvcOAefx+5y5iqhPxq5KC4G1RaCI+toiV+0KgUJggyOApHuY0fGIiLq3hiKsyEJIRTzRG9zYBTLAg6DOcEfSEfOLLrqoeTeRJGE5LEoWCKpSs8AIZCGYxa/PmPvQ581nsO69BQa81BUCwzAUUa/boBAoBJYsAjzmRx11VDtqkJdPCInIUYlLdnAzGI4M5VcEW1/kESZlIVIzNK3iQmCdEEDIXT53Yveb2P3nTP0tttiiyPo6IVyNC4F3IvBb/+dTVqEQKAQKgSWIgK8vp524EPUQVbGgPntpl+DwJppsTMZnQWJsCDqilK/yjH1i4yosBNYBAfdY7j/3mXtP3v1nYeySrntwHUCupoXACIEi6iNAKlsIFAJLB4Hsy0ZY40mX7re/yC+XgBQhR/m1IGM2vp6sL5fx1jimDwH3XBaHkwj5cvq8TR/6ZdFKRKC2vqzEWa8xFwLLBAFEATEQ9548ZUht6pbJcNsweiKU8RurMIk4Laex11g2PAK5//rPlvuv7r0NPzdlwfJEoDzqy3Nea1SFwIpHoMjDir8FCoBFQqA+W4sEbKktBCYgUER9AihVVAgUAoVAIVAIFAKFQCFQCGxoBJbP5s0NjWT1XwgUAoVAIVAIFAKFQCFQCCwgAkXUFxDMUlUIFAKFQCFQCBQChUAhUAgsFAJF1BcKydJTCBQChUAhUAgUAoVAIVAILCACRdQXEMxSVQgUAoVAIVAIFAKFQCFQCCwUAkXUFwrJ0lMIFAKFQCFQCBQChUAhUAgsIAJF1BcQzFJVCBQC6x+BvB1x3LMj5FwVphcB85P5k/YyHaHmbXrnrCwrBAqB9YtAvfBo/eJdvRUChcAiIYDw9cELWEL46mUsPTIbPm1e+itvVc185c2XG97SsqAQKAQKgQ2L4cvPxwAAIABJREFUQBH1DYt/9V4IFALrgEC8sT0pj7qQvkl1kal4wyAQkm5usohSJm1Oi6hvmHmpXguBQmD6ECiiPn1zUhYVAoXAPBEIGSfuleYInhBynvqQwXmqLbFFRCCEPHOSxVbKbX/hYa9QCBQChUAhMAxF1OsuKAQKgSWLALL33HPPDU899dTws5/9bPUe534rBQIfUrhkB7qMDM/iyZDMS4h68up33nnnYY899lhGo66hFAKFQCGwdggUUV873KpVIVAITAkCd91113DZZZcNb7/99rDxxhs3zzrTeGaLoE/JJI3MMC+5EPP8EvLzn/98eP3114ejjz66iPoIs8oWAoXAykSgiPrKnPcadSGwLBBA9p588snhwQcfHPbcc89hr732akQdaUfU3/Wud61+oHRZDHgZDWK8iELYn3322eHee+8dNttss2U00hpKIVAIFAJrj0AR9bXHrloWAoXABkYA2eOFRcgPPvjg4fTTT2/7m3/xi180L20R9Q08QTN0H5KebTCJV61a1Yj6W2+9NUPLKi4ECoFCYGUhUER9Zc13jbYQWJYIvPvd7x4233zzYeutt25EPUTQ/vSQwGkbOI8/29joSsiebWPoy1O/HOLMj7EYLyyM1XMG733ve1dvhVkOY60xFAKFQCGwLggUUV8X9KptIVAIbHAEPDjqCuFNeoMbNsEApNT105/+dPjJT37SCOoHPvCBttWD/TzJyv1K8J73vGfYdNNNh/e///2rFxtkkHs6xg/MKlMf0qt7hDj5nhxPMG2DFbErthmTYCwVCoFCoBAoBOrUl7oHCoFCYIkjEJI3yTudumkYIvtcb7zxxnD//fcPd9xxx2CLzgEHHDAcdthhbfvOo48+Otxzzz3Da6+9Nuy0007DQQcdNOywww6NgPdjoUeITnWT6vvytEHmpyWwiY0IugUFgh47p8XGsqMQKAQKgQ2JQHnUNyT61XchUAgsOAKI3zSSvdj05ptvDrfffvvw9a9/vRHTc889t51wovyqq64arrjiilb+oQ99qD0gqx0CmwtgSSO40tom2AakjctCQAwTBD0e68hOS8y+CoVAIVAIFALvRKCI+jsxqZJCoBAoBBYUgZDtbF158cUXh7vvvrsRZ1tdHEl42223DZdffnnztDu9xskntsVo+9JLLw3PP/982xIj7yFZW2K23377RsA9hMkjvckmmwy77rprI+a2zzgRx75vx1bav08fUlzEeEGnt5QVAoVAIbBoCBRRXzRoS3EhUAgUAr9EALl2CWKk2n50+9DlvbCJN92Z8Dzihx9++HDooYc24o3U33DDDY3Ia0OeZ9zDs8cee+xw4IEHDpdcckkj8gj+Jz/5yba3/emnnx4uvvji4Yknnmgn4hx//PHD+973vqn1qte9UggUAoVAIfBOBIqovxOTKikECoFCYMERiBfbVhVB3tYUhPqaa64ZbrrppkbebXk57bTT2pnw6m+55Za2Tcb54ltssUXzpGujDgnnQf/xj388XHTRRW0LzZFHHtn2tt93333D+eef3+p44JH/CoVAIVAIFAJLC4HpeapoaeFW1hYChUAhMG8EbHlBzJF03nRBGQ+5/eoXXnhh86rvvPPOjaTzptva8txzzw1XXnnl8MMf/rC9edWDp8ccc0zbyuIlTzztL7zwwsBb/uqrrw533nln0ydta40tMcJ2223XvOw88VkwtIr6UwgUAoVAITDVCBRRn+rpKeMKgUJgOSBgu0pIegi7cSHqjz32WPN6S9uXzkMuRujtMecZR7ztM7d1BcFH4unzJk/1Rx111LDlllsOr7zySiP1jzzySCPsTo/Zfffdh3322adtlZnWh0mXwxzXGAqBQqAQWAwEiqgvBqqlsxAoBAqBDgHkPF51ZDn71JUj31tttVXzdNvSwguOmL/99tvtIVIPktrmoswe9h/96EftlJd99923Hd2oznnrRx99dNvfzqtuu4xjHuknt+OOO7Z+5Kc9LAUbpx3Dsq8QKASWDwK1R335zGWNpBAoBKYYAURdEIe0ewvnbrvt1rzdXoJkr/n3vve9RqwR73jhyTvh5eSTT24PmDrRJV71Qw45pJV95jOfaafGIPu2yzzzzDNty4ttNE58QYAtEKaJCMemTFtsS5zyiguBQqAQWKkIFFFfqTNf4y4ECoH1jgDCHfKtc9tZPPxp64pw9dVXt73l9q07wUW9LS0ItsA7vvfeezei79hFW1tskUFsvRxpl112aV53Z7F7sdIJJ5zQTnxxQoy+KxQChUAhUAgsLQSKqC+t+SprC4FCYAkigJwj2yHL4qSRcV7vjTbaqO0xv/XWW4dvf/vbbavKEUcc0Y5gfPjhhwf7zr/yla+001u04X33dtNPfepTrf222247fOxjH2tbZ15++eW2z51e5Y587PtcghCWyYVAIVAIrEgEiqivyGmvQRcChcD6RKDfyoGw2/KyzTbbNPIs7UVETnP5vd/7vbY33bnq1157bfOqn3LKKYOz1G+++ebhgQceaKfDIN0ePqXXJW8rDKL+ta99bfASJdtdDjvssLatRr1+LRjSZn2Ov/oqBAqBQqAQWDsEiqivHW7VqhAoBAqBNUYAWUbKTz/99MFRjEizLS5ItreKnnPOOW3PuiMXvQxpp512anJ/+Zd/2facezupLS8uD6Husccebe+6c9JtgfFQqT7UnXvuue1lSLzviLpQJH2Np6waFAKFQCGwQREoor5B4a/OC4FCYCUgwJPtdBZbUBB1bxNF0AWEnFfdaTC87M5Ed+IL4q3Olhje8R122GHwEKmgjjxCnm0tvOhf/vKX25GNCLsjGbVHzpH3BPkKhUAhUAgUAksDgSLqS2OeyspCoBBYwgggx7zeCTzoroQQaeQbMRe0yYOi2mZ7S4i3NklbCPCy87gj70i9IxkR9njTxeQrFAKFQCFQCCwdBH79n2Pp2FyWFgKFQCHwGwggrXlgMzGBaSGmsY9tIezKerKNlCPTKWN/yHXKxL1cSDgPPJJ+9tlnt1NkeOh57Xnvkf9gEvnfAG8KMsYVG6fAnDKhECgECoGpQaCI+tRMRRlSCBQCa4MAkoeoOofcmzmRc2QW8ZN2IashuKnXDmlWZ0tJT5K1DUkeE0jyQsr7/Ez26ytX5MkqY0/0JS3fp5vAr/5ow7bYqNjYjOXggw9uxzSqs+2lxyM6Z9Lb19OXfpRLCyH6sZsuW3oE41IenJOPnkk6tQ/O5sBDs2+++Wb7JaAprT+FQCFQCKxwBIqor/AboIZfCCx1BBDAZ599drj++uuH119/fTVRNK6Qw5BGpNCe7uwBRxQRXCRROqQyBFIeEdWODvpCkNVJCyGwi40lu2YKbOu99RkPO10Js+kgk/oQaG2Dozo4GHf23Gsjr+8eE2XaBXPysdEcqHfRScYcePvqY4891h6gjb0VFwKFQCGwkhEoor6SZ7/GXggscQRCQBFvJ6U4WxwhtPUDCUT+EEuXgChKk0cspZUJyGKIZk9I0wd90tqQjb6W6Ahu8hs6NobYnjg2qZsUIhfyLG/cgrRxBzPY5kFWGPZtIhsbgl3KQ+rNQ9rRYZ+9FzUpq1AIFAKFQCEwDEXU6y4oBAqBJYsAQocsOi3l8MMPX/2GT2QSOUTaQ6xDFrWRVo44IoghnPLqhBB3ZSlXFpKubNoI5ULYFB0ZszFmnImDJSyUTcKs9+6nvr/R+nZJ2/rCo57FUy9f6UKgECgEViICRdRX4qzXmAuBZYIAMulyUsqee+7ZXhqEgAupQwKlkb+ePCKZIYTa9GnyQtr2+pDOENTIkFsfYa5+YvdC2DLWlTyc2JEFS+L0GTkysBInTUaaTN9OmUUVkr7lllu2X0Kir+JCoBAoBFYyAkXUV/Ls19gLgWWCAKKHhDvyMGS8Hxpi2BN1Wy682ZMn3UOXiDqiGELJs0tms802G7wwKORSmYs+ZdrrT9q12GFt+ghxnq9t5DM+ZBrZjkdc/9Iw8NCnepgr10YezrCNDvjASeiJe9qItaPTXEi7KhQChUAhUAjU1pe6BwqBQmAJI4AUIn+IHcInJEYUEyKjTNr+6jvvvLOR7P3226+dMhJPvAdS77rrruG1114bDjjggGH33XdvOj3oaA+8y8uFENTddtut1fMC2xe/mCHjWtM++nY9JrPp0cYVvMTwgZ3LUZBw2GqrrYa999674UgGeX/kkUcafnBE0Lfbbrth3333bWe7y5MLEZce59nV2zybnVVXCBQChcByR6A86st9hmt8hcAyRgDJQxzFfQgB7MuQP0Ty0UcfbUT9vPPOayRy++23b+eNI4/a8QaT4VXfdttt2wkkiP2tt946XHvttcMzzzzTvMY88PbGf+hDH2pvE11sot6PZTHTcIKpEMIsNl6YeGjXQubee+8djjvuuGGPPfZonnDyTt+57LLLhh/+8IetrS1JFjRHHnnkcOaZZ7aFTcg+vEPYx2XpfzHHWboLgUKgEFgKCBRRXwqzVDYWAoXARARsq4gnPGS9J+khmgihNC+vYxydLIJMHnvssY10p010IPRkbMcQ4mV/+OGHGzHda6+9Gpm///77h9tvv33Yf//9295qsiGfdPH4I7jKpF3S3h6KjNIrJuvlRP02Gu1cbOCJRngF8hYO7HNKChntePXpjQzdFg/w0W+2ltAFC3q0Tf/k6In9yqWDIdknnnhiuOOOO4brrruu7SeHA92xCT4333xza4ec2zaE0N99990DWW9M1T95gf70DwN9pf8mUH8KgUKgEFjhCBRRX+E3QA2/EFjKCCB2IZLj2LiUIYC5kFHk0cuREF2EN3JpTxZ5DJkU8yTzFm+66aaN3COhDz30UNsC8+STTzYCy7Pc60BstUNuEf+XX355eOmll4ZNNtmkvZhIPzfeeGOzhV3HHHNMeyAWubbtxhYSuulB0pFc23CQcR5/bXn36dGvh2l5uP1CYGsOgsyjbay2qhiv9rb6bLHFFs0z/sADD7Rx6cP+cFtZjMN2lWxTodvFRjLs86uDPoKr2MIAJrYInXTSScPHPvaxJs8Gv0YYj7elso8+hDy2Jx/clVcoBAqBQqAQqD3qdQ8UAoXAMkAgZHI8lBBJ5cgo0ohEPv3008NXv/rV1UQz7ftYG+15opHt5557rhHYnXbaadh6660bMUVs6XrqqaeaZ5lHOn1aBNjHfdFFFzVCTV/OCQ9ZRl4ReBfS/dnPfrZ5xm+44YbhBz/4QStHmuO1PuWUU9o2G8T7qquuagsND7wi9ldffXWz4/d///cbMbcFBaHWp1gbZP/jH/94O8rylltuGa688spGuI1bH5tvvvnwwQ9+sGFkjFmsINXGtssuu7SFhnGxXRt1SDwbHn/88Za3J52s9rYH6V8dmRD1fq70H0+6NkXUe3QqXQgUAisZgfKor+TZr7EXAsscAYQP8UMCkUGE0r5z5Fua1zgEERSTCKL2CCbizbOtjRDvsgUAb3K2qPREU7ntILzZH/3oR4cdd9xxuPjiixt5t+3m7LPPbu2+853vtP3vRx99dPOAX3PNNY2k85AfdNBBzUt9ySWXDFdccUV7wNVDrB/+8Icb6UWu7Rv/4he/OHzzm98czj333GbrPffc0+KjjjpqOOywwwbbdGz3sXXFNhtEne2xyxh5w22hgZVgLMFN3q8BPPraG68rgefeLwZw4bEXwwzBR9SDUXSmj7SvuBAoBAqBQuCdCBRRfycmVVIIFALLBAFk0IUcIuYJfXk84Il7oh05nmMEFSnmlUfuySO6yCpCGtIaPWSQVOR+5513Hs4666ymg2fbQ6kIOGJOnlceyea55wHnfeatR+zZY3GgXw9x3nfffe0BVgQcMUaQeeQRYV558llU2KJz+umnt5NZLFBsQUHGXVl8wATx5rlnr60tCHnsV8/GLGj6GKbq9AkL/WrPVjYrt9WIPrJkMp7MRcWFQCFQCBQCMyNQRH1mbKqmECgEljgCiLaAHCKhAmIZAt6nW+WEPyGgIZnaCHSEpIpTjsgmTY5n2fYPxBvhR1rZIo/Qss0CAJFFnrVHwJF1BDx2I/h00WEbjj3qttXII8X2s2tLnwthRs6R/ZwHr73Aa26/OA/9f/3XfzWZgw8+eDjkkEPaPvZ+DBmb8SpPLJ08ndJstWCw2GBXcI5s67z+FAKFQCFQCMwbgSLq84aqBAuBQmApIoAkJiCwIdFi5DhkUiwknzbxliOfiLQ4ZFhMB297tsSkPf2RIyMkJiNNhn1pK21BgPA6w/3EE09sdbz1ZBFvBJ/3/cILL2wnqZDzAChibG873Ug6+ZBlaeV0C7zcHl7Vn/PkkXxvBeWxt6XGlhuLh+DFVu0Fccpbwa9IukWAfj1kas++7T5kLTZ48C1KyOhTe3GFQqAQKAQKgdkRKKI+Oz5VWwgUAkscAWQx5FKMtLqQRSTchcAio8iji1yIJFKLIAv2giPr5J3kYtsJWVtHQo7pTlCXEHKa/mODflKG8PN+a4fYHnrooW1LiraxkQ22v/C6//3f/317QBSxv+CCCxoxp498tuLoH2EP2U5/vPwnn3xy27/udBpHLiLqHhK1pz22i4MFPexgrz7p1JfLFh+LCEcx8vjzrGtLt3on5hgfXdEdbCouBAqBQqAQmIxAEfXJuFRpIVAILAMEQoARRWlE0xYSRy0inMgsIolEIsjZGtITSWW77rrr4LQXXmL7yD0s6ShC3mKnm+yzzz6NuKZd+gWhtBACLe4vtmmH9CL7jlC0X9zJKkgvbzt5xJz9CDybyfN6WzBYPCDZdAnk+kA2Xnky9rIj0sqN2xhstUHShdisPrhp59eEV155pbXVB085LJ0mA0NHRNp/7wHaVatWtXEZBwx5/eEWbIwpfQU3+T7dBOpPIVAIFAIrGIEi6it48mvohcByQACBRP5C8OSRwBBC5S55JJPn2YkoTiJBNL/xjW+0c809dIlwCkg8PWlrT7ctJs4md3KKoxHp4lXmfXbkYN9n2qpHTnncE8gh2DzQ6sny2usDKee9t1f80ksvHc4///zhpptuakSXreo+8YlPtIdDLRj+4z/+o6mlA1lH8JFrF32IvzHoE1lGphF9wakvToIhZ988Yk0OBmS0E+hO7Nx1RzraYkMfz75fJGyXQcTtc/cAq4dWv/SlLzV9FjfKPTzb45D56WN9wSR9t47rTyFQCBQCKxiBIuorePJr6IXAUkcAoRbGxI63FwFEWNUlRgKRUsTa0YjZh43QCiGl0Sfvsk3E+eIILLLOo+0hTeTziCOOaGS3KfjVH+31hTg7nYUsEk6XoxUdiehNnciuMSC5yC5vOmIvzYNvrzcCThcdytj+mc98pnnBEWc2IfbOZuclR/oF+8zpk2cPvaeeemqL9Y2UBye2IdP0i7Vhq3bkhJB9HnhjYrutLBYc5OgwjjPOOKNhb4sOGXbZa6+ODvMi1kYQJ61P9RUKgUKgECgEfolAEfW6EwqBQmDJIoDwIYiCrR2IJ1Iewicdjy0yiKQff/zxjVxrk3ox0p62ZNNOjJAimsgucs4bj6B6KRCPtLQQwhndSLU6xDfklB598Y4rczm+8bTTTmseZ15n5Fs94p2HMpFe5dqSsQjwECgSj/zzbNuawmuuTy92Ihfb2G5POhuV02OrShY7cETC2UqncZNlHzzFtshom18cMk66LXbgZOFir7qHSumBDy+9dsGHvn6O4K6ODXQbS4VCoBAoBAqBejNp3QOFQCGwhBFA6pBzpE8IEQy5TLl8iCfPdOSUCfQgwilHVhFZxBOJdEkjxwh0dNGLjKZdbFDvQpK1S//0WCwoj23KEHBEN32pYwM5uqNfrD/62MHTL2irTfqVz3Yc5doZHwJNhg52hTwrI5fxsCPeduWCMosAdiVop40QG+ncf//9W3vl2qnLIipyaUdGH/0eerZWKAQKgUKgECiiXvdAIVAILGEEkL0QUeQTcQwhRBDlExBE8i7ptFOfOjGiaT+6E114gqMn7ciMg376cun+0pf25FxsZSeZ1PEmS8eu3ta0VWdRIc8ueUHcE2L1gr7SNvbIu7QJ6SfHHoFc325cFt3k0iZlkWUL3WQS6OxD8mkrzqVthUKgECgECoEi6nUPFAKFwBJGICQaYURgeWVtmwjZDOGUR0wRwZBHbXpym3Kxvd308WiLXWNd0UeHQB8Z7aMreXZliw5d6Ve9PGIq7WIj3ZGLd1mZIE4f2unXFhly2keXckFe//TqVzndQsqktY1uaX30ePU61KcNffSmTWxLvZge9fpVP7YxdhkHudjeOqk/hUAhUAisYATKbbGCJ7+GXggsdQSQOgTy6aefHi677LIWhwwihz3xRP4QRAExDPEk41KWENKZvFjZpIB4TgrpXx2b5Huvubyg78TKYoc2+kyZdG+XdupcGYMxWlxYrKStMcvTq3/jplue7WOdbElfZKI/hFw+GKuPbOJgnDH17TLWnsynjLx5dPqMt6ZWKAQKgUKgECiPet0DhUAhsMQR8HCmU0+QRieN9CQUSQwpRCQFMVkBSZQnF9IbuUkEPHXapl6ZSz56oy9x+tVHdOhbXpuelNMTmcTpix5txnaHgCu3390DqPRqjzizQ0hZ+qY3uvo+xv2SUR/7055OaaFv3+fpcmkb29Ne3tgFvwhYUDiT3qkyFQqBQqAQKASKqNc9UAgUAksYAeTQKSzIKU8xIhoSaFghyiGRY9IYAqtNiOhMxHM2mEJs9d/3m/5DUMnpx5UFhbrY0dtJT/J939GlLOPJuOVDeCMnjn3pu89Hx6S++j7oIROsUtfj3denL3LBNLboM/0Zu7QHYJ1aI1h8VSgECoFCoBAYht/6v3xjFxqFQCFQCCxBBHhh33zzzdVk0BAQv56AhhSOy8Zff2m3NjDQhYgK0SumM3qT72VCXvs+0z5293XKxmQ5ctrRl/pxf5FL/8n3cn1fSc9Ur1yIHuleNuXK+vLojbzYYiOk3fYdxL1CIVAIFAIrHYEi6iv9DqjxFwJLHIGQxcRLfDgr1nykPnMoHZK/YgGpgRcChUAhwBFSHvW6DwqBQqAQKAQKgUKgECgECoHpQ+CXv9NOn11lUSFQCBQChUAhUAgUAoVAIbCiESiivqKnvwZfCBQChUAhUAgUAoVAITCtCBRRn9aZKbsKgUKgECgECoFCoBAoBFY0AkXUV/T01+ALgUKgECgECoFCoBAoBKYVgSLq0zozZVchUAgUAoVAIVAIFAKFwIpGoIj6ip7+GnwhUAgUAoVAIVAIFAKFwLQiUER9Wmem7CoECoFCoBAoBAqBQqAQWNEIFFFf0dNfgy8ECoFCoBAoBAqBQqAQmFYEiqhP68yUXYVAIVAIFAKFQCFQCBQCKxqBIuorevpr8IVAIVAIFAKFQCFQCBQC04pAEfVpnZmyqxAoBAqBQqAQKAQKgUJgRSNQRH1FT38NvhAoBAqBQqAQKAQKgUJgWhEooj6tM1N2FQKFQCFQCBQChUAhUAisaASKqK/o6a/BFwKFQCFQCBQChUAhUAhMKwJF1Kd1ZsquQqAQKAQKgUKgECgECoEVjUAR9RU9/TX4QqAQKAQKgUKgECgECoFpRaCI+rTOTNlVCBQChUAhUAgUAoVAIbCiESiivqKnvwZfCBQChUAhUAgUAoVAITCtCBRRn9aZKbsKgUKgECgECoFCoBAoBFY0AkXUV/T01+ALgUKgECgECoFCoBAoBKYVgSLq0zozZVchUAgUAoVAIVAIFAKFwIpGYGqI+v/93/8NrkkhdX39TGnte/lxOvXpJ3oSj8sjHz2pH8epH+sZyyUfefmk+7Ypi/ykuJePnsR93Tjd5yfpTVnkxvGk+l5GetI1bicfuXE6suO472dct6Y6Zmrf6+nti3zKEqc8cV/ep3u943Sf79tI96GvS3kv06ejcya5SbLRnzhtE4/Lx/lxn2k3WzzWIT9TGMuSm1Q2U/uZyif1uSZ6e9k+PbZvUl1sSl3icflM+fTRx5FNTGfCJP2pG8djWfV92Vxp9eM26aNvG5k+jlzKxrqS7+UmpSOX/pLvZVOXsnFeed8u9ZPi6EibyKR8rCdyfX1k+rZ9OrKJU5d2Ke/jvm4sn3wvP1O6l01aLPRx6sZ6xuWT8n2bcX3fTy83V3qSnuhS16cnyaYssn1/fVmf7mX6dGQS93V9elwvPy6LfMojk3zqJ8W9TNqRS3ocT9KRssgm3+vpyyq95gi8a82brF0Lk5jwW7/1Wy3Zl/3P//zPoPy3f/u331H3v//7v61MvWt8Q0TPTHXK+zCWV6d/fY91JN+379N0RYad/+//zW/tExvo6tPRTRe90Z3yPh63622JXK9HmXHGRrqF6JnUl7pckR3blT5S35RO+EMufbFh3F/q+qZjGyOTuJeVnlQeHanPXI/bkstY6OntC2bR0ffT16Ve3LdPX3274NHf8+qVj8syhr59dEZenJC+yY/bpi6yieEijMeTenHun+gY2zPuK21TLj9uw+6+Xj42pJ/E47b0vf32200+mKXPSXHfT3RFdy8/Lhvne1np6Bqnk1dvTOJf/OIXw7vf/e6mYlI7ZWM7lRmfuG/TlHT9p21kYncwTT7txKnry5KOnuTFfdk4LZ9xSmcc4zmmRxmZd73rXb8xLvP5nve85zf66dv3ffZ2zZSOvHimsUYmOsgJuQ9nqs/40m4cT/pM9TYk3evv070dKU+ffT7pcf/jfOTEdNPVz5e0ssiN28v3dXTIj3HqZcY6xnWxg5y+5XOvj21Jfqxj3Mek/Ext
a. The greatest number of pies sold on any day was 30.
a. What is the rule for the table below?
b. What is the missing input?
c. What is the missing output?
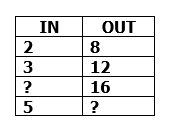
a. X 4 (times 4)
b. 4 (4 x 4 = 16)
c. 20 (5 x 4 = 20)
Which numbers are prime?
31, 49, 17, 18, 67, 86
31, 17, 67
What is the correct order for following the order of operations?
1. parentheses, multiplication, division, addition, subtraction
2. parentheses, addition, subtraction, multiplication, division
3. multiplication, division, addition, subtraction, parentheses
4. addition, subtraction, multiplication, division, parentheses
1. parentheses, multiplication, division, addition, subtraction
a. Chord
b. Circle
c. Radius
d. Diameter
Diameter (d)
What is the mean of the data below:
2, 3, 4, 5, 5, 7, 9
Numbers in the data set = 7
(2 + 3 + 4 + 5 + 5 + 7 + 9) = 35
35 / 7 = 5
mean = 5
Which word describes the letter "p" in the expression below?
9 x p
a. whole number
b. operation
c. algebra
d. variable
d. variable
Which numbers are composite?
45, 7, 9, 67, 18, 27, 31
45, 9, 18, 27
Evaluate the following expression following the order of operations:
8 (7+2) - 3
8 ( 9 ) - 3
72 - 3
69 = answer
What time is 12 hours and 20 minutes after 11:15pm?
11:35 am
What is the mode for the data below:
2, 5, 8, 9, 3, 5, 4, 7, 8, 5
least to greatest = 2, 3, 4, 5, 5, 5, 7, 8, 8, 9
mode = 5
Which of these could be solved using the open sentence 7 - 2 = h?
a. Ryan had 7 hamsters. Each hamster had two babies. How many hamsters does Ryan have now?
b. Ryan had 7 hamsters. Then bought two more at the pet store. How many does he have altogether?
c. Ryan had 7 hamsters. He gave each of them 2 treats. How many treats did he give them in all?
d. Ryan had 7 hamsters. He gave two to a friend. How many does he have left?
d. Ryan had 7 hamsters. He gave two to a friend. How many does he have left?
7 - 2 = h
Which of the below numbers are odd?
11, 22, 35, 67, 88, 89, 90, 92, 96, 97, 45, 47, 38
11, 35, 67, 89, 97, 45, 47
Evaluate the following expression using order of operations:
6 - 2 + ( 8 -3 ) x 7
6 - 2 + ( 8 -3 ) x 7
6 - 2 + ( 5 ) x 7
6 - 2 + 35
4 + 35
39 = answer
What is the name of the triangle if there are two identical sides and one angle greater than 90?
a. Obtuse Scalene
b. Obtuse Equilateral
c. Obtuse Obtuse
d. Obtuse Isosceles
d. Obtuse Isosceles
What is the median of the data below:
2, 5, 9, 3, 5, 4
least to greatest = 2, 3, 4, 5, 5, 9
middle numbers are 4 and 5
(4 + 5) = 9
9/2 = 4.5
Kathleen has three times as many seashells in her collection as her friend Gabby. Gabby has 15 seashells. Which number sentence could be used to find k, the number of seashells that Kathleen has?
a. k = 15 - 3
b. k = 15 x 3
c. k = 15 + 3
d. k = 15/3