Geometry
Estimathon
Math Trivia
Puzzles!
100
What postulate proves that the triangles are congruent?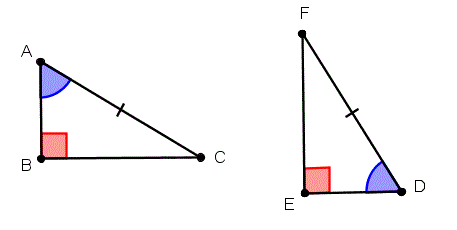
AAS
100
Current Population of the USA
~343,073,753
100
Who developed the Cartesian coordinate system?
Rene Descartes
100
A must ferry a wolf, a goat, and a cabbage across a river. His boat can only carry one item at a time besides himself. If left alone, the wolf eats the goat or the goat eats the cabbage. How does he get all three across safely?
1. Take the goat across.
2. Return, take the wolf across, and bring the goat back.
3. Take the cabbage across, return, and bring the goat across.
200
Four identical squares and one rectangle are placed together to form one large square as shown. The length of the rectangle is how many times as large as its width?
4/3
200
What is the cost of the most expensive single McDonalds item in the world (in dollars as per 2021)?
27.19
200
Who is considered the first female mathematician?
Hypatia of Alexandria
200
You are outside a room with three light switches. Inside the room are three light bulbs, each controlled by one switch. All of the light bulbs are turned off before you begin. You may only enter the room once. How can you determine which switch controls which bulb?
Turn on two bulbs (A, B) for a long time, then shut one of them off (A). The lit bulb is the one that was on the whole time (B). Out of the two unlit bulbs, one (A) will be warm and the other (C) will be cool.
300
Crystal has a running course marked out for her daily run. She begins this run by heading due north for one mile. She then runs northeast for one mile, then southeast for one mile. The last portion of her run takes her on a straight line back to where she started. How far, in miles, is this last portion of her run?
sqrt(3)
300
What is the farthest from any land one can be in the ocean (in miles)?
1680.7
300
This famous Iranian mathematician became the very first woman to win the Fields Medal for mathematics in 2014.
Maryam Mirzakhani
300
Four people must cross a bridge at night in 1, 2, 7, and 10 minutes. Only two can cross at a time, and they must use a single torch. Thus, each pair travels at the slower person’s speed. What’s the fastest total time and how?
17 minutes. 1 and 2 cross, 1 returns, 7 and 10 cross, 2 returns, and 1 and 2 cross.
400
[AMC 10A 2004] Square ABCD has side length 2. A semicircle with diameter AB is constructed inside the square, and the tangent to the semicircle from C intersects side AD at E. What is the length of CE?
5/2
400
What is the number of ways to tile the 4 × 4 square with 1 × 2 and 2 × 1 dominoes?
36
400
How many zeroes does googolplex have?
Googol (10100)
400
500
Triangle 
has 
. Let 
and 
be on 
and 
, respectively, such that 
. Let 
be the intersection of segments 
and 
, and suppose that 
is equilateral. What is 
?
90
500
What is the number of stations in the entire New York subway system? Transfer stations count as multiple stations.
472
500
According to the film The Hitchhiker’s Guide to the Galaxy, this number is associated with life, the universe, and everything.
42
500
You have a balance scale and 12 coins, 11 of which are genuine and identical in weight; but one is counterfeit, and is either lighter or heavier than the others. How can you determine the counterfeit coin and whether it is lighter or heavier in the least amount of weighings? (you'll need an explanation!)
It will take three weighings.
First, group the coins in three groups of 4 (1-4, 5-8, 9-12). Weigh groups 1-4 and 5-8 against each other. Case 1: If the scale is balanced, those eight coins are all genuine. Proceed by weighing any two genuine coins against coins 9 and 10; if they balance, one of coins 11 and 12 is the counterfeit. Otherwise, one of coins 9 and 10 is counterfeit. Out of the two possible fakes, simply weigh one of them against a genuine coin and you'll know which is the counterfeit and whether it is light or heavy. (another option is to weigh three genuine against three unknown and go from there)
Case 2: If the scale is not balanced after the first weighing, we know that coins 9-12 are all genuine. WLOG, say that coins 1-4 are lighter than coins 5-8. The counterfeit is either one of 1-4 and light, or one of 5-8 and heavy. Weigh coins 1, 2, 5 against 3, 6, 9 (or any other genuine coin) for the second weighing. If balanced, then the counterfeit is either 4 (heavy), 7 (light), 8 (light). Weigh 7 against 8; if balanced, 4 is the counterfeit, otherwise, the lighter coin is the counterfeit. If the second weighing was not balanced and the 1, 2, 5 group was heavier, then the counterfeit is 1 (heavy), 2 (heavy), or 6 (light). Weigh 1 against 2; if balanced, 6 is the counterfeit, otherwise, the heavier coin is the counterfeit. If the second weighing was not balanced and the 3, 6, 9 group was heavier, either 3 (heavy) or 5 (light) is the counterfeit. Weigh either one against a genuine coin to find the counterfeit.