This mathematician famously died a virgin.
Who is Sir Isaac Newton?
The equation represents the unit circle.
What is x2 + y2 = 1?
You solve this to find the area under a curve.
What is an integral?
Roots of the characteristic equation.
What are eigenvalues?
The probability of drawing two cards of the same suit from a standard deck.
What is
12/51
This triangle is named after a famous French mathematician.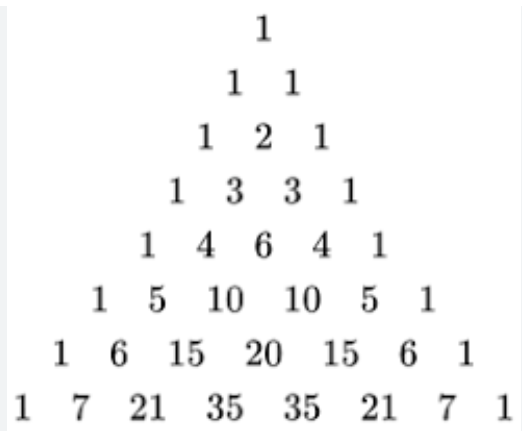
Who is Pascal?
A function where each input value is mapped to a unique output.
What is a one-to-one function?
This series, named after a French mathematician, expresses a periodic function as an infinite sum of sines and cosines.
What is the Fourier Series?
The ninth number of the Fibonacci sequence.
What is 21?
The base-10 value of this binary number 10110.
What is 22?
Einstein said the best part of his day was walking home from work with this mathematician.
Who is Kurt Gödel?
This mathematical structure is a set equipped with two binary operations that satisfy associativity, distributivity, and the existence of additive and multiplicative identities.
What is a ring?
This theorem asserts that any bounded sequence in R^n has a convergent subsequence.
What is the Bolzano–Weierstrass Theorem?
Rank of the coefficient matrix is the same as the augmented matrix
What is consistent?
The rule for finding the probability of an event A given event B.
What is P(A|B) = P(A, B)/P(B)?
This mathematician moved from society, became a wizard, and created modern algebraic geometry.
Who is Alexander Grothendieck?
The condition that occurs when in a topological space, every open cover of the space has a finite subcover.
What is compactness?
What is a Cauchy sequence?

This theorem states that every continuous map from a closed disk to itself has at least one fixed point.
What is the Brouwer Fixed Point Theorem?
The effects of two variables on the response cannot be distinguished from each other.
What is confounding?
This mathematician was tricked into defending their doctoral thesis after 10 years of work.
Who is Stefan Banach?
In algebraic topology, this property describes a space in which every map from the unit interval I=[0,1] into the space can be homotoped to a constant map, making it a contractible space. This property implies that the space has trivial fundamental and higher homotopy groups.
What is contractibility?
This is an example of this phenomenon?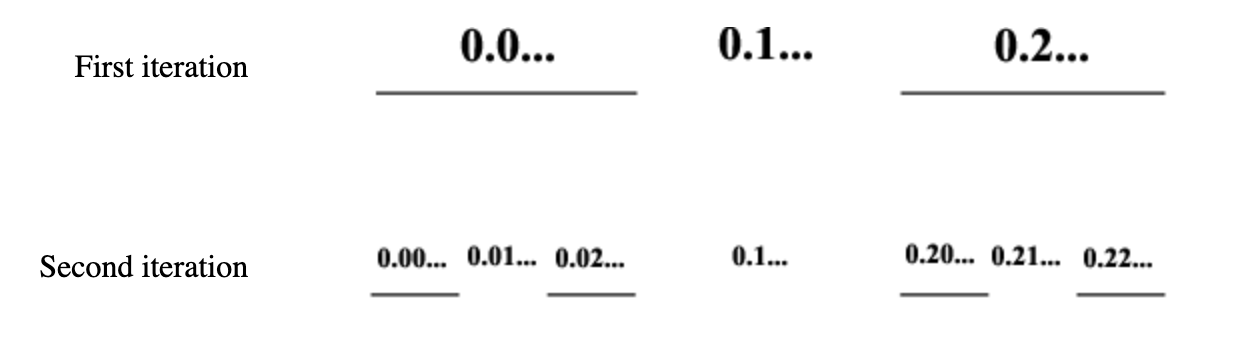
What is Cantor dust?
Determines homomorphism of cyclic group.
What is the generator of the cyclic group?
This distribution has the special property that the expectation and the variance are the same.
What is a Poisson distribution?