Rationale Zahlen und Potenzen
Geometrie
Terme und Gleichungen
Prozent- und Zinsenrechnung
Wachstumsprozesse und Formeln
100
Ordne die Zahlen der Größe nach:
-7/8; 9/8; -13/16
-7/8 < -13/16 < 9/8
100
In welchem Quadranten liegt der Punkt P=(-3/4)?
4. Quadrant
100
Erkläre die Begriffe Variable, Äquivalenzumformung und Lösung einer Gleichung.
Variable = Platzhalter für Zahlen
Äquivalenzumforung: Rechenoperationen ohne dass sich die Lösung einer Glg ändert.
Lösung: Was darf für Variable eingesetzt werden so dass Glg. stimmt
100
Erkläre den Unterschied zwischen Grund- und Prozentwert.
Grundwert entspricht 100%, Prozentwert entspricht p% (Prozentsatz) des Grundwerts.
100
Handelt es sich hier um ein direkt proportionales Verhältnis? Begründe!
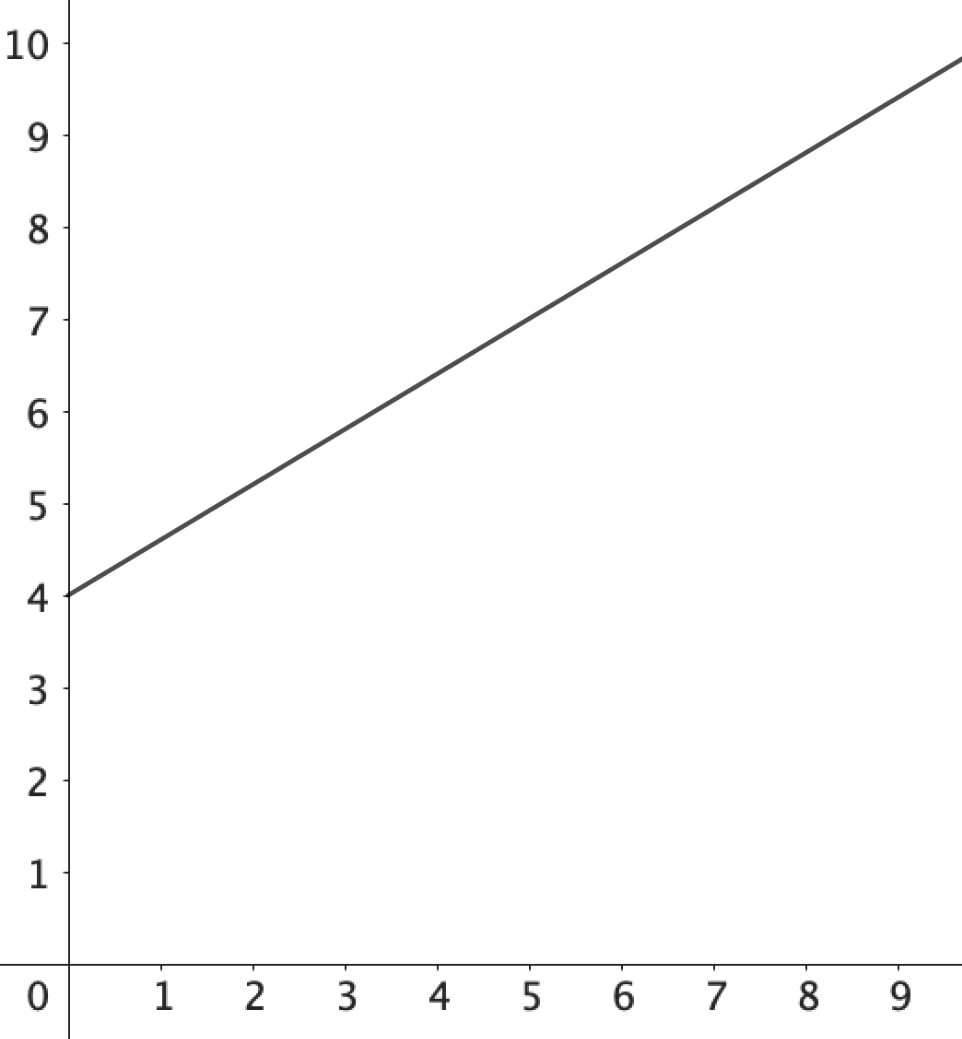
Nein: es ist zwar eine Gerade, diese geht aber nicht durch den Koordinatenursprung!
200
Berechne den Doppelbruch:
(4/5) / (12/10)
2/3
200
Welche der besonderen Vierecke sind auch ein Parallelogramm? Nenne alle!
(Quadrat, Trapez, Raute, Rechteck, gleichschenkliges Trapez, Deltoid)
Quadrat, Rechteck, Raute
200
Berechne den Wert des Terms!
T(2)=4*a - 2*a + 3
T(2) = 7
200
Ein Pullover kostet ohne MWSt. 50€. Wie viel kostet er mit MWSt.?
(In Ö: 20%)
60€
200
Ein Taxipreis setzt sich aus der Standgebühr S=5€ und den Kosten k=0,90€ pro km zusammen. Berechne den Preis für eine Fahrt von 4km, wenn für den Preis P (nach x gefahrenen km) folgende Formel gilt:
P=G+k*x
P=5+4*0.9=8,60€
300
Berechne: (-2/3)^3
-8/27
300
Erkläre den Begriff Trapez und gib die Formel für den Flächeninhalt an!
Viereck mit einem Paar paralleler Seiten.
A=(a+c)*h/2
300
Berechne - fasse so weit wie möglich zusammen!
(3-2t)^2
9-12t+4t^2
300
Ein Verkäufer bietet dir folgende Optionen an - erkläre welche (und warum) für dich besser ist!
Option 1: -10% und dann nochmal -20%
Option 2: direkt -30%
direkt -30%, da die -20% sonst von kleinerem Grundwert.
300
Gegeben ist folgende Formel - schreibe diese in die Form 'm=...' um!
G=p*m-K
m=(G-K)/p
400
Berechne: -2/4 - (3/4 + 8/12)
-23/12
400
Bei einem Rechteck verhalten sich die Längen wie 3:4. Die längere Seite ist 12cm lang. Wie lang ist die kürzere?
3:4 = x:12 => x=9cm
400
Löse die Gleichung:
z - 19 = 2-2z
z=3
400
Ein Kapital liegt auf einem Sparbuch. Erkläre die folgende Formel im Detail! (jede Zahl).
K_1=1000+1000*253/360*5/100*0,75
253/360 -> Kapital liegt 253 Tage am Konto
5/100 Zinssatz sind 5%
0,75 Kest
Insgesamt wird das Kapital nach 253 Tagen berechnet.
400
Wie lange braucht ein Auto mit einer Geschwindigkeit v=50km/h für eine Strecke von 5km.
Lösung muss in Minuten angegeben werden!
t=s/v=5/50=1/10=6/60 => 6min
500
Schreibe die Lichtgeschwindigkeit ( \approx 300 000 {km}/s ) in Gleitkommadarstellung in der Einheit
m/s
3*10^8 m/s
500
Für die Zahlen a=1, b=2 und c=3 - Welches der Vierecke hat den größten Flächeninhalt?
Quadrat: mit Seite a
Rechteck: mit Seiten a, b
Parallelogramm: mit Seiten a, b und ha=c
Raute: mit Seite b und Höhe h=c
Raute
Quadrat:1
Rechteck: 2
Parallelogramm: 3
Raute: 6
500
Löse die folgende Gleichung und gib die Lösungsmenge an!
(a-5)^2=5*(5-2a)+a^2
Wahre Aussage. Jede Zahl ist Lösung.
500
Stelle eine Gleichung auf - nehme als Variable d für den Gewinn des dritten Platz.
Das Preisgeld beträgt 1200€ und wird so aufgeteilt:
1. Platz: Um ein Viertel mehr als der Zweite
2. Platz: 100€ mehr als der Dritte
4. Platz: 25% weniger als der Dritte
1200=0,75*d+d+(d+100)+(d+100)*5/4
500
Wie lange braucht ein Motorrad um von 80 {km}/h auf 90 {km/h} zu beschleunigen, wenn die Beschleunigung mit a=2 {km}/{h^2} gegeben ist.
Verwende die Formel: v=v_0+a*t .
t={v-v_0}/a=10/2=5s