Who's that polynomial?
It didn't go to school, but it has a degree
Simplifying isn't always so simple
Is it a function?
Gears in the function machine
100
A polynomial with one term
Monomial
100
The degree of a term when it has no variables
0
100
3x + 2x
5x
100
A type of relation where each input value has exactly one output value
Function
100
When a function is written as an equation and y is replaced with f(x)
Function notation
200
A polynomial with three terms
Trinomial
200
When terms in a polynomial are written in descending order of degree
Standard form
200
xy + 6xy
7xy
200
The input values of this set:
{ (1,3) , (5,2) , (1,5) , (2,3) }
1, 5, 2
[any order]
200
The output value of this function when the input is -1
-4
300
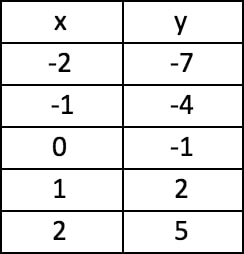
A classification for this polynomial:
x + 1
Linear and/or Binomial
300
A polynomial with a degree of two
Quadratic polynomial
300
(x + 2) + (x - 9)
2x - 7
300
A method used to determine if the graph of a relation is a function
Vertical line test
300
In the given relation, these ordered pairs are the reason it's NOT a function:
{ (3,5) , (2,9) , (9,5) , (2,10) }
(2,9) and (2,10)
400
A classification for this polynomial:
7x³ + 1
Cubic and/or Binomial
400
The degree of:
x + x² + x³
3
400
(x + 2) - (x - 9)
11
400
The output values of this set:
{ (6, -1), (-2, -3), (1, 8), (-2, 5) }
-1, -3, 8, 5
[any order]
400
The output value of this function when the input is -2
2
500
The operation that a polynomial can't include
Division
500
The degree of:
nm⁴ + sj⁶ - s²y⁵n
8
500
(x³ + 2x² + 3x - 2) - (2x³ - x² - 4)
-x³ + 3x² + 3x + 2
500
At x = 1, the relation has this many outputs
2
500
The output value of:
f(⅔) = x²
⁴/₉