Matrix Operations
Inverse, Determinant and Systems
What is a Linear System with 3 variables?
Properties
Systems of equations Word Problems
100
[2 3 5] + [3 5 8] = ?
What is [5 8 13]
100
Find the Determinant of the following matrix:
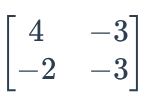
-18
100
A system of linear equations with 3 variables will have this many solutions to find.
what is 3
100
How many rows and columns are in the following matrix?
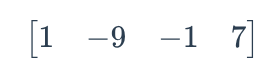
1 row, 4 columns
1 x 4
100
At a particular restaurant, each slider has 350 calories and each onion ring has 40 calories. A combination meal with sliders and onion rings has a total of 11 sliders and onion rings altogether and contains 1370 calories. Write a system of equations that could be used to determine the number of sliders in the combination meal and the number of onion rings in the combination meal.
x + y = 11
350x + 40y = 1370
200
Do the following, and determine the element a22 of result:
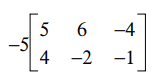
What is a22 = 10?
|-25 -30 20|
|-20 10 5 |
200
Find the inverse of the following matrix:
200
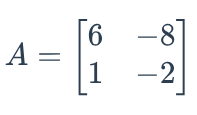
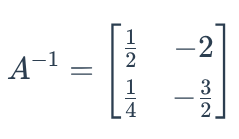
Write the following Augmented matrix as a system of equations.
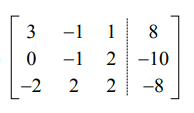
3x - y + z = 8
-y + 2z = -10
-2x + 2y + 2z = -8
200
What is a number in a matrix called?
An element
200
Valeria has $2.60 worth of dimes and quarters. She has a total of 14 dimes and quarters altogether. Write a system of equations that could be used to determine the number of dimes and the number of quarters that Valeria has.
x + y = 14
0.10x + 0.25y = 2.60
300
[5 4] - [2 -3] = ?
What is [3 7]
300
Find the area of a triangle with the following coordinates (-3, 3), (2, 4) and (3, -1)
13 square units
300
Solve the following system of equations for all three variables
{(x,+3y,+9z,=,4),(-x,+8y,-6z,=,4),(x,+3y,+3z,=,10):}
what is
x=10, y=1, z=-1
300
A matrix with m rows and n columns
What is a m x n matrix?
300
A publisher needs to send many books to a local book retailer and will send the books in a combination of small and large boxes. Each small box can hold 25 books and each large box can hold 35 books. A total of 15 boxes were sent which can hold 455 books altogether. Determine the number of small boxes sent and the number of large boxes sent.
7 small boxes
8 large boxes
400
When multiplying the following matrices(A & B), what is the output at c21?
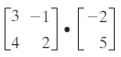
What is c21 = -8 + 10 = 2
400
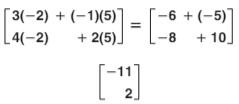
Find the solution of the systems of equations using the elimination method
{(-x,-2y,=,4),(2x,+8y,=,-28):}
what is
(6,-5)
400
Solve the following system of equations for all three variables
{(-9x,+6y,+4z,=,-10),(-9x,+5y,+4z,=,-8),(9x,+y,-3z,=,1):}
what is
x=2, y=-2, z=5
400
What has to be true when adding or subtracting two matrices?
They have to have the same dimensions
400
Shaquana and her children went into a movie theater and she bought $53 worth of candies and pretzels. Each candy costs $5 and each pretzel costs $3. She bought a total of 13 candies and pretzels altogether. Determine the number of candies and the number of pretzels that Shaquana bought.
7 candies
6 pretzels
500
Mechanical pencils cost $4.95, pens cost $2.99, and notebooks cost $3.49. Olivier bought 12 mechanical pencils, 8 pens, and 7 notebooks. Paulina bought 6 mechanical pencils, 12 pens, and 9 notebooks. Use matrices to find the total amount Olivier spent.
500
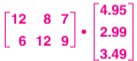
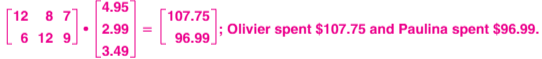
Find the solution of the systems of equations using the elimination method
{(-x,-8y,=,49),(-x,-2y,=,7):}
what is
(7,-7)
500
Solve the following system of equations for all three variables
{(-8x,+7y,-8z,=,-9),(-8x,+7y,-10z,=,-7),(x,-2y,+z,=,9):}
what is
x=-4, y=-7, z=-1
500
What has to be the true when multiplying two matrices?
The number of columns in the first matrix has to be equal to the number of rows in the second matrix.
500
The community college soccer team sold three kinds of tickets to its latest game. The adult tickets sold for $10, the student tickets for $8 and the child tickets for $5. The soccer team was thrilled to have sold 600 tickets and brought in $4,900 for one game. The number of adult tickets is twice the number of child tickets. How many of each type did the soccer team sell?
200 adult tickets, 300 student tickets, and 100 child tickets