Identify element a23 from A =
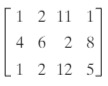
2
(Triple points) Give me a matrix A where AB = B given B =
[[31, 21] , [63, 57]]
This is known as the Identity matrix I. A =
[[1, 0], [0, 1]]
What is the matrix from of
{[2x+3y=8], [4x-y=5]}
[[2,3],[4,-1]][[x],[y]]=[[8],[5]]
What is the rule for determining if two matrices can be added or subtracted together?
The matrices have to be the exact same dimensions (equal number of rows and columns)
Can the following matrices be multiplied together? How do you know?
[[1,2],[3, 4],[5, 6]] [[1,2, 3],[4, 5, 6]]
Yes, because the first matrix is a 3x2, and the second matrix is a 2x3. Since the second matrix has the same number of rows, as the first one has columns (2), these matrices can be multiplied together.
Find the determinant:
[[6,4],[-9,3]]
54
(Double Points) Give me a matrix A and matrix B where AB = BA. The matrices cannot be identity or zero matrices.
Need to use diagonal matrices.
Example: AB=BA
[[2, 0] , [0,3]] [[4, 0] , [0, 5]] = [[8 , 0] , [0, 15]]
[[4, 0] , [0,5]] [[2, 0] , [0, 3]] = [[8 , 0] , [0, 15]]
What is the solution of the matrix equation
[[5,3],[2,1]][[x],[y]]=[[-5],[1]]
[[2],[-5]]
Simplify the following matrices based problem: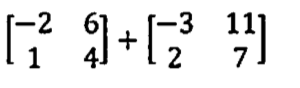
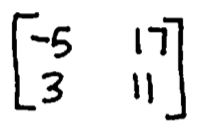
Solve the following operations:
2[[1,-2],[-3, 4],[5, -6]] + [[-7,8],[9, -10],[-11, 12]]
[[-5,4],[3,-2],[-1,0]]
This matrix has the same number of rows as columns.
Square Matrix
(Single Points) What is the inverse of
[[3,2],[4,1]]
[[-1/5,2/5],[4/5,-3/5]]
What is the solution of
[[-6,-3],[8,4]][[x],[y]]=[[144],[-64]]
no solution
Given Matrix X and Matrix Y. What is Y-X?
Matrix X=
[[2,-3],[-1,4]]
Matrix Y=
[[-4,1],[3,-2]]
[[-6,4],[4,-6]]
What is AxB?
Matrix A=
[[1,1],[1,1]]
Matrix B=
[[0,3],[4,4]]
[[4,7],[4,7]]
Find all three separate determinants:
[[-4,3],[-1,2]] , [[6,4],[-2,3]], and [[-8,-5],[3,0]]
-5, 26, and 15
(Single Points) Give me a matrix A and B with 2x2 dimensions where AB = 0
[[1, 1] , [0,0]] [[2, 3] , [-2, -3]] = [[0 , 0] , [0, 0]]
Solve the System using matrices
4x - y = 19
5x - 5y = 20
(5, 1)
Subtract:
[[1,-2, -1],[-3, 4, 3],[5, -6, -5]] - [[-2, 1, 2], [4, 3, -4], [-6, -5, 6]]
[[3,-3,-3],[-7,1,7],[11,-1,-11]]
What is AxB?
matrix A=
[[4,3],[9,7]]
matrix B=
[[6,3],[9,4]]
[[51,24],[117,55]]
Write a 4x4 identity matrix
[[1,0, 0,0],[0,1, 0,0],[0,0,1,0],[0,0,0,1]]
Create matrices for the following system of equations:
x - y + z = 0
x +2y - z = 0
2x + y - 3z = 0
Then solve whatever way you would like.
[[12, 4, -7],[-2, -1, 5],[3, -8, 6]] and [[-12, -4, 7],[2, 1, -5],[-3, 8, -6]]
x = 0, y = 0, z = 0.
Later in our unit, we will solve matrices using Gaussian Elimination, Inverse Matrices, and Cramer’s Rule
Solve the following using matrices
5x - 2y = 18
3x - y = 7
x=-4
y=-19
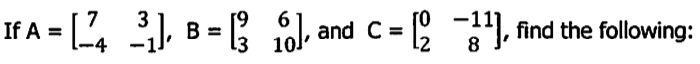 2C + A
2C + A
What is
|7 -19|
|0 15|
Solve the following multiplication:
[[1,2, -2, -1],[-3, -4, 4, 3]] xx [[5],[6],[7],[8]]
[[-5],[13]]