Geometri
Statistikk
Funksjon
Pytagoras
100
Hva er benevningen for volum og areal?
Volum: opphøyd i 3. Eks: cm3
Areal: opphøyd i 2. Eks: cm2
100
Hva heter sentralmålet hvor du finner ut hvilket tall/ord/observasjon som opptrer flest ganger?
Typetall
100
Hva kalles en funksjon der grafen er en rett linje?
Lineær funksjon
100
Hva er formelen for Pytagoras-setning?
Kat2 + Kat2 = Hyp2
a2 + b2 = c2
k2 + k2 = h2
200
Hva er formelen for overflateareal av et prisme?
2lb + 2bh + 2lh
200
Hva er variasjonsbredden i klasse A og B?
I to klasser ble elever spurt hvor mange ganger de har fritidsaktiviteter i løpet av en uke. Dette ble svarene:
Klasse A: 1, 2, 4, 2, 3, 6, 7, 3, 2, 1, 5, 2, 6, 2
Klasse B: 3, 4, 5, 6, 2, 4, 6, 4, 8, 2, 4, 6 ,3, 2, 0
Klasse A: 7-1 = 6
Klasse B: 8-0 = 8
200
Hva er konstantledd, stigningstall og variabel i denne funksjonen? f(x) = 50x + 200
50 = Stigningstall
X = Variabel
200 = Konstantledd
200
Hvis du skal finne lengden av den ene kateten, hvordan vil formelen se ut da?
hyp2 - kat2 = kat2
300
Hva er volumet av dette prismet?
30 m3
300
Finn medianen:
1 2 4 1 0 1 2 2 2 2
2 2 1 3 2 2 0 1 2 0
1 0 1 2 2 3 0
2
300
Bestem funksjonsuttrykket til grafen under.
y= 3x + 2
300
Hva er spesielt med en 30° -60° -90° trekant og en 45° -45° -90° trekant?
30° -60° -90° = den korteste kateten er halvparten så lang som hypotenusen
45° -45° -90° = katene er like lange
400
Hva er omkretsen av denne sammensatte figuren?
13,2 cm
400
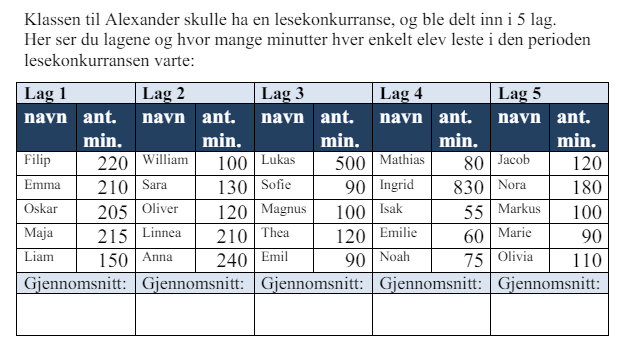
Regn ut hvor mye hvert lag leste i gjennomsnitt.
Lag 1: 200 min
Lag 2: 160 min
Lag 3: 180 min
Lag 4: 220 min
Lag 5: 120 min
400
Hva forteller de to grafiske fremstillingene om de to pristilbudene? (hva lønner seg? startpris, stigningstall, funksjonsuttrykk)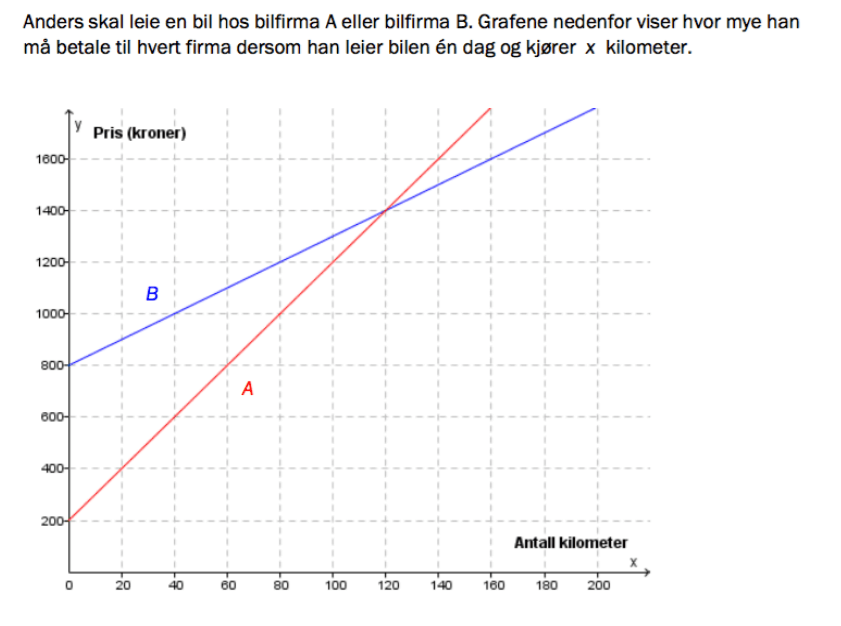
Bilfirma A:
Konstantledd/startpris for å leie = 200 kr.
Stigningstall: 20 km øker med 200 kr, men vi vil finne for 1 km, dvs at vi deler 200/20 og får 10 kr i stigning i pris per km (x).
Funksjon er da: y= 10x + 200
Bilfirma B:
Konstantledd/startpris for å leie= 800 kr.
Stigningstall: etter 120 km stiger prisen med 600 kr, vi vil ha for 1 km, og deler derfor 600 på 120 = 5 kr i prisstigning per km (x).
Funksjonsuttrykk: y = 5x + 800
Altså, etter 120 km koster det like mye å leie hos begge firmaene (1400 kr). Hvis du har tenkt å kjøre under 120 km, lønner det seg å velge Bilfirma A, men hvis du skal kjøre lenger enn 120 km lønner det seg å velge bilfirma B.
400
Regn ut de ukjente sidene i trekanten (AB og AC).
AC= 3,5 x 2 = 7 cm
AB =
hyp2-kat2 = kat2
72 - 3,52 = kat2
49 - 12,25 = kat2
36,75 = kat2
kat = 6,1
AB = 6,1 cm.