Quadratics
Exponential
Logs
Calculus
Mystery
100
Factorise
x^2 + 5x + 6
x=-2
x=-3
100
Evaluate 25
32
100
Solve log525
log525 = 2
100
dy/dx x^3
3x2
100
Differentiate
y=2x^2 -8x +7
y' = 4x -8
200
Factorise
x^2−7x+10 =0
x =2
x=5
200
Evaluate 32 x 34
= 36
=729
200
log2x = 3
x=8
200
dy/dx 5x^2 -4x + 7
= 10x - 4
200
Solve log2(x-1) = 5
x = 33
300
Factorise
2x^2+3x−5
x = 1 or x = -5/2
300
Solve for x
4x = 16
x=2
300
Solve log101
log101 = 0
300
Find the gradient of the curve at x=3 for the following function
y=x^2 + 2x
Gradient at x =3 is 8
300
The graph of y=log4x is shifted left 2 and up 1. Write the new equation.
y= log4(x+2) +1
400
Find the discriminant of the following and state the number of solutions.
x^2+6x+9=0
discriminant = 0
therefore, 1 real root
400
A population of bacteria doubles every 3 hours. If there are 100 initially, how many after 6 hours?
Population after 6hrs = 400
400
Solve log39 + log33
log39 + log33 = 3
400
Differentiate y=(3x -1)(x2 +2)
y'=9x2 -2x + 6
400
Find equation of the tangent at x=4 for y=x2 +1
y = 8x-15
500
Expand and simplify: (x+2)(x−5), then determine the axis of symmetry of the resulting parabola.
x=3/2
500
Sketch the general shape of y=2x — state the y-intercept and horizontal asymptote.
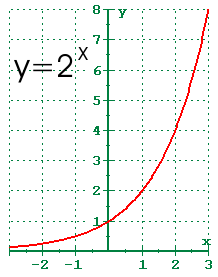
y - int = (0,1)
Horizontal asymptote - y=0
500
The graph of y=log3x is translated 3 units to the right. Write the new equation
y=log3(x-3)
500
Differentiate
y= (5x-3)/x^2
y'= (-5x^2 + 6)/x^4
500
Find the stationary points of y=x3 - 6x2 +9x
Stationary points are located at (1,4) and (3,0)