Reciprocal Trig Ratios
Special Angles
Angles Greater than 90
CAST Rule
100
What is the reciprocal trig ratio for
sinθ ?
cosθ ?
tanθ ?
cscθ = 1/sinθ
secθ = 1/cosθ
cotθ = 1/tanθ
100
What shape do you cut along its diagonal to get 2 congruent right isosceles triangles? What are the angles in the resulting triangles?
Square
45o, 45o and 90o
100
What are the 2 conditions for an angle to be considered in standard position?
vertex is at origin (0,0)
initial arm is on the positive x axis
100
For the CAST rule, state the quadrant and the trig ratio(s) that are positive in that quadrant
quadrant 1 sinθ, cosθ, tanθ, cscθ, secθ, cotθ
quadrant 2 sinθ, cscθ
quadrant 3 tanθ, cotθ
quadrant 4 cosθ, secθ
200
Match the trig ratio with its definition
cscθ adjacent/opposite
secθ hypotenuse/adjacent
cotθ hypotenuse/opposite
cscθ hypotenuse/opposite
secθ hypotenuse/adjacent
cotθ adjacent/opposite
200
What shape do you cut along its height to get 2 congruent right scalene triangles? What are the angles in the resulting triangles?
Equilateral Triangle
30o, 60o and 90o
200
Which axis is the related acute angle relative to?
x axis
200
The terminal arm passes through the point (-8, 6) what quadrant is it in? Find the primary trig ratios for θ
Quadrant 2
sinθ = 6/10
cosθ = -8/10
tanθ = -6/8
300
Determine the value of θ to the nearest degree
cscθ = 1.4526
θ = sin-1 (1/1.4526)
θ =44o
300
Match the following
sin30o 1
tan45o √3
cos30o 1/√2
tan60o 1/2
cos45o √3/2
sin30o 1/2
tan45o 1
cos30o √3/2
tan60o √3
cos45o 1/√2
300
What direction does the principal angle go in?
CCW
300
The terminal arm passes through the point (8, -15) what quadrant is it in? Find the six trig ratios for θ
Quadrant 4
sinθ = -15/17 cscθ = -17/15
cosθ = 8/17 secθ = 17/8
tanθ = -15/8 cotθ = -8/15
400
Determine the value of θ to the nearest degree
secθ = 3.2404
θ = cos-1 (1/3.2404)
θ =72o
400
BONUS 500 points
Determine the exact value of the following trig expression
cos60o (tan60o) + tan45o (sin60o)
= 1/2 (√3) + 1 (√3/2)
= √3
400
What direction does a negative angle go in from the initial arm?
CW
400
BONUS 400 points
cosθ = 0.8829 find positive values for θ between 0o and 360o
θ = cos-1(0.8829)
θ = 28o
360o - 28o = 332o
quadrant 1 and 4 cosθ is positive
so θ = 28o and 332o
500
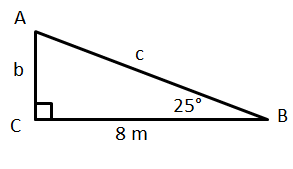
For the triangle above, use a reciprocal ratio to determine the length of the hypotenuse to the nearest tenth of a metre.
sec25o = c/8
c = 1/cos25o (8)
c = 8.8m
500
Determine the exact value of the following trig expression
sin30o x tan60o - cos30o
= 1/2 x √3 - √3/2
= 0
500
If the terminal arm is in quadrant 1, state the 6 trig ratios in terms of x, y and r
sinθ = y/r cscθ = r/y
cosθ = x/r secθ = r/x
tanθ = y/x cotθ = x/y
500
sinθ = 5/12 find positive values for θ between 0o and 360o
θ = sin-1(5/12)
θ = 25o
180o - 25o = 155o
quadrant 1 and 2 sinθ is positive
so θ = 25o and 155o