Functions, Domain, and Range
Characteristics
of Functions
of Functions
Average Rate of Change
Function
Transformations
Transformations
Function
Representations
Representations
100
Write the interval shown on the number line. 
(-∞, 2]
100
Determine the absolute minimum of the graph.
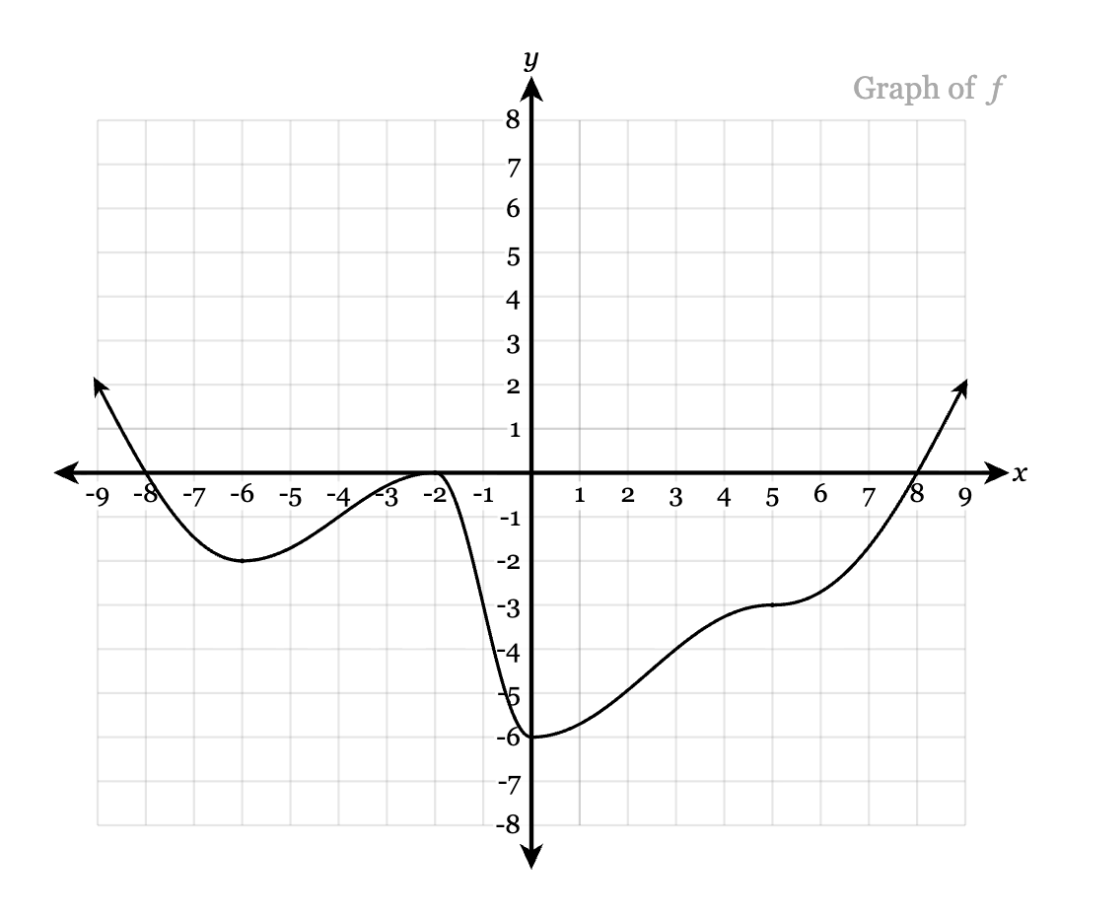
-6
100
What is the average rate of change from x = -6 to x = 4?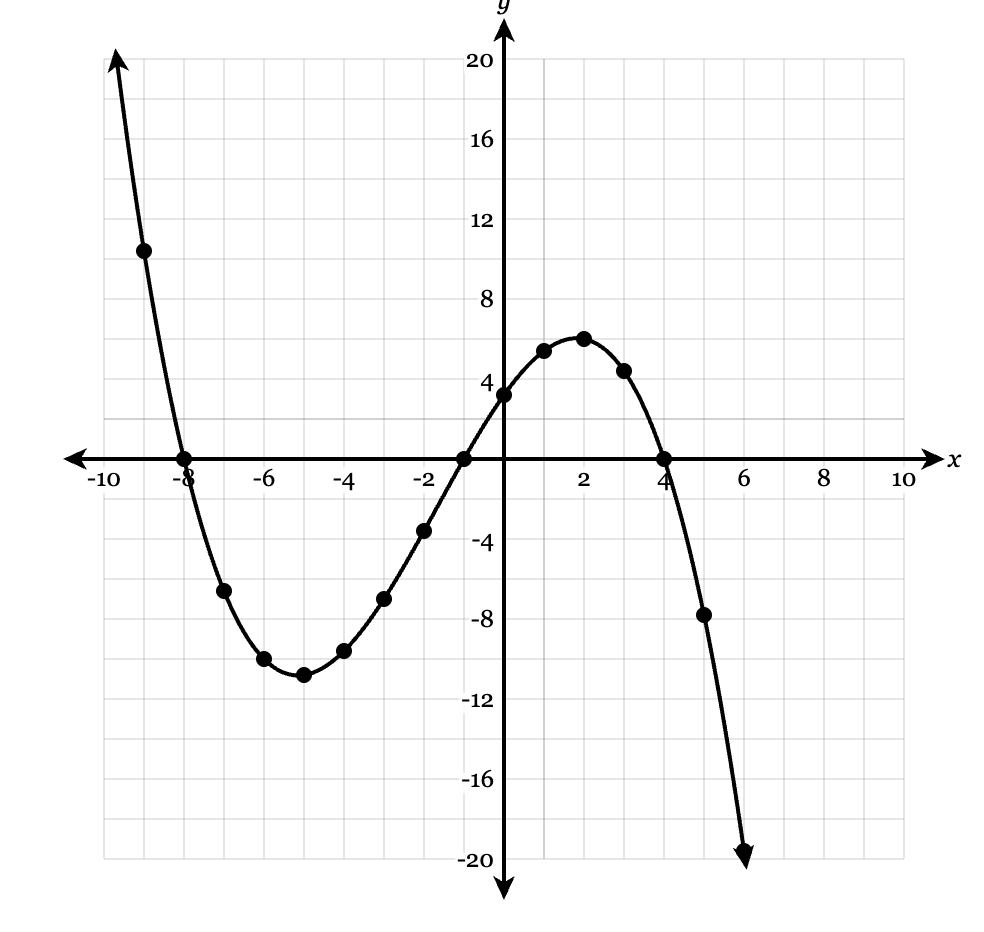
1
100
Write the equation of g(x) which is a transformation of f(x) shifted 5 units to the right.
g(x) = f(x - 5)
100
The graph represents the path of a rock being launched from inside a volcano. How long does it take for the rock to land on the ground?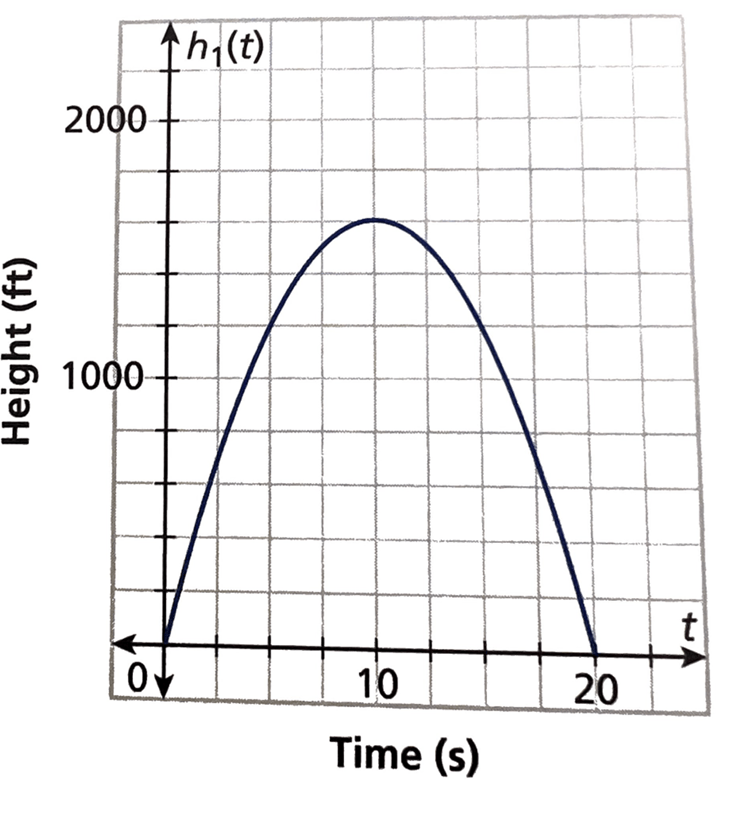
20 sec
200
The interval notation for all real numbers.
(-∞, ∞)
200
How many points represent a relative maximum?
2
200
Determine the average rate of change between 1 sec and 3 secs.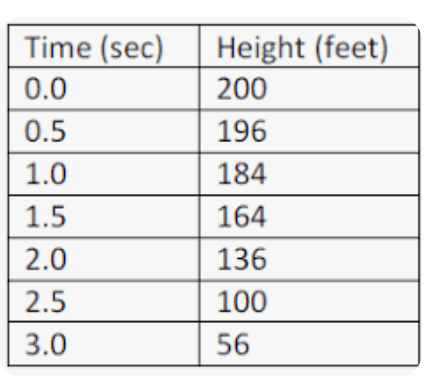 
-64 ft/sec
200
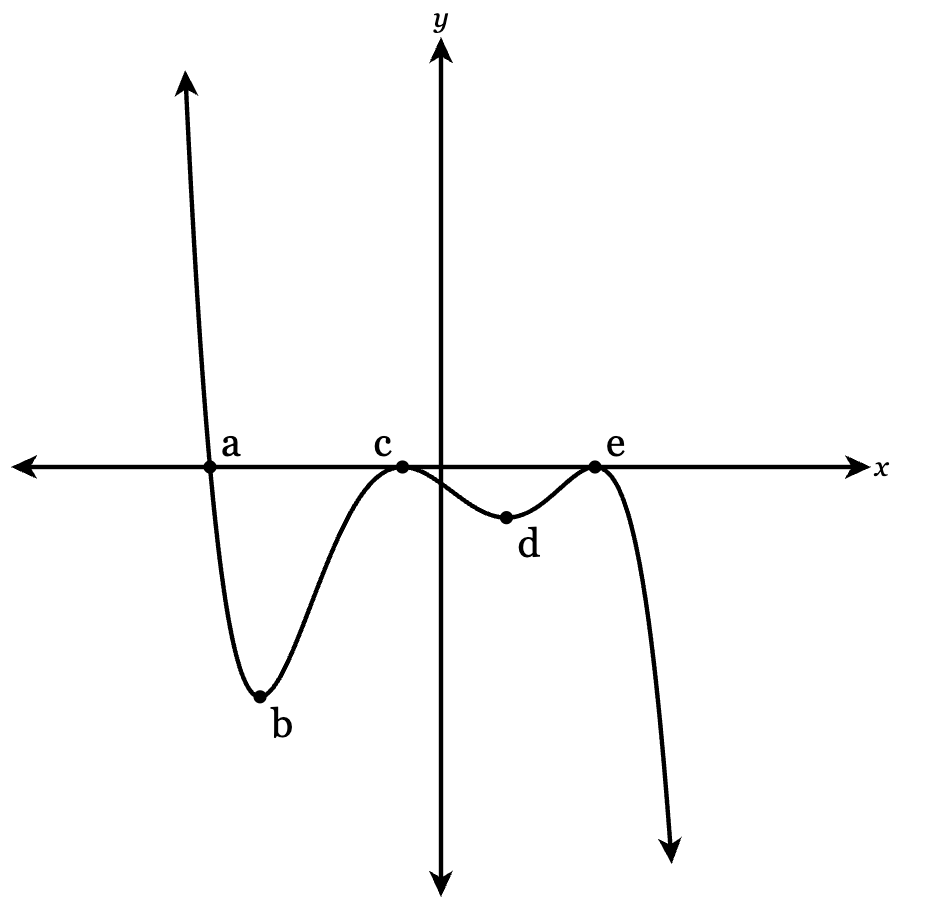
Given the graph of f(x), sketch the transformed function g(x) = -f(x).
200
The graph represents the path of a rock being launched from inside a volcano. What is the maximum height reached by the rock?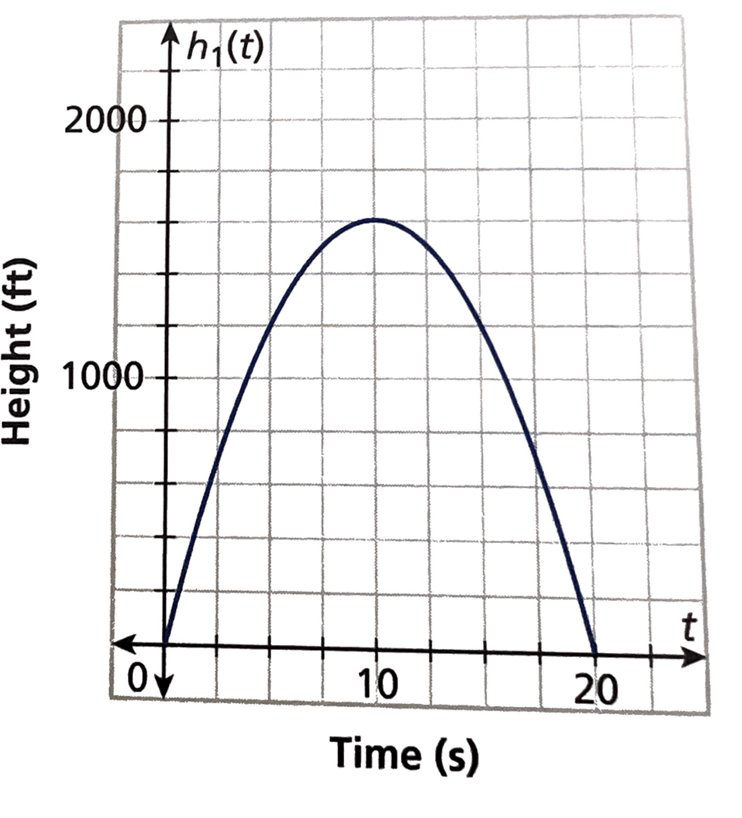
1600 ft
300
The domain of this function.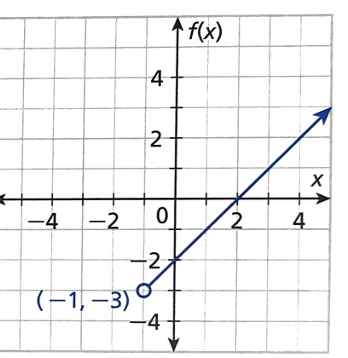 
(-1, ∞)
300
Determine the domain where the function is increasing.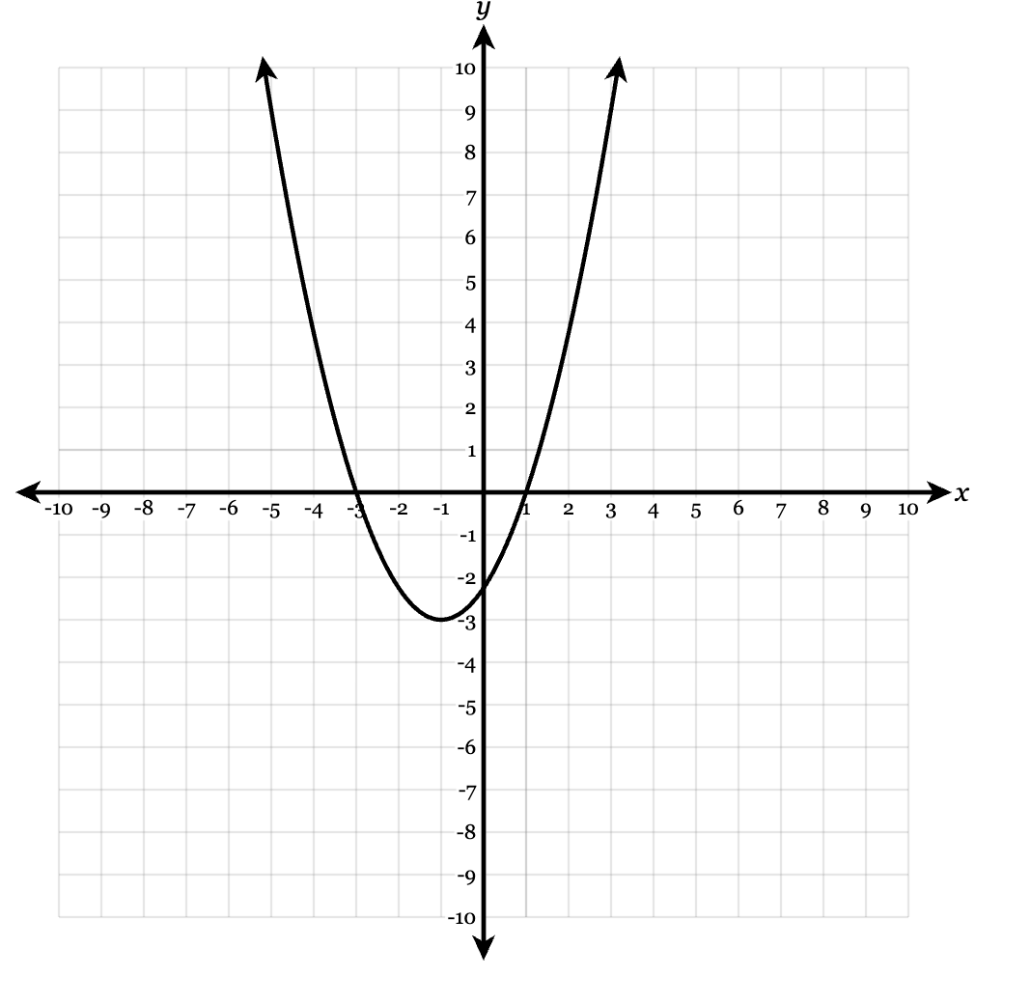 
(-1, ∞)
300
What is the average rate of change from -2 to 6?
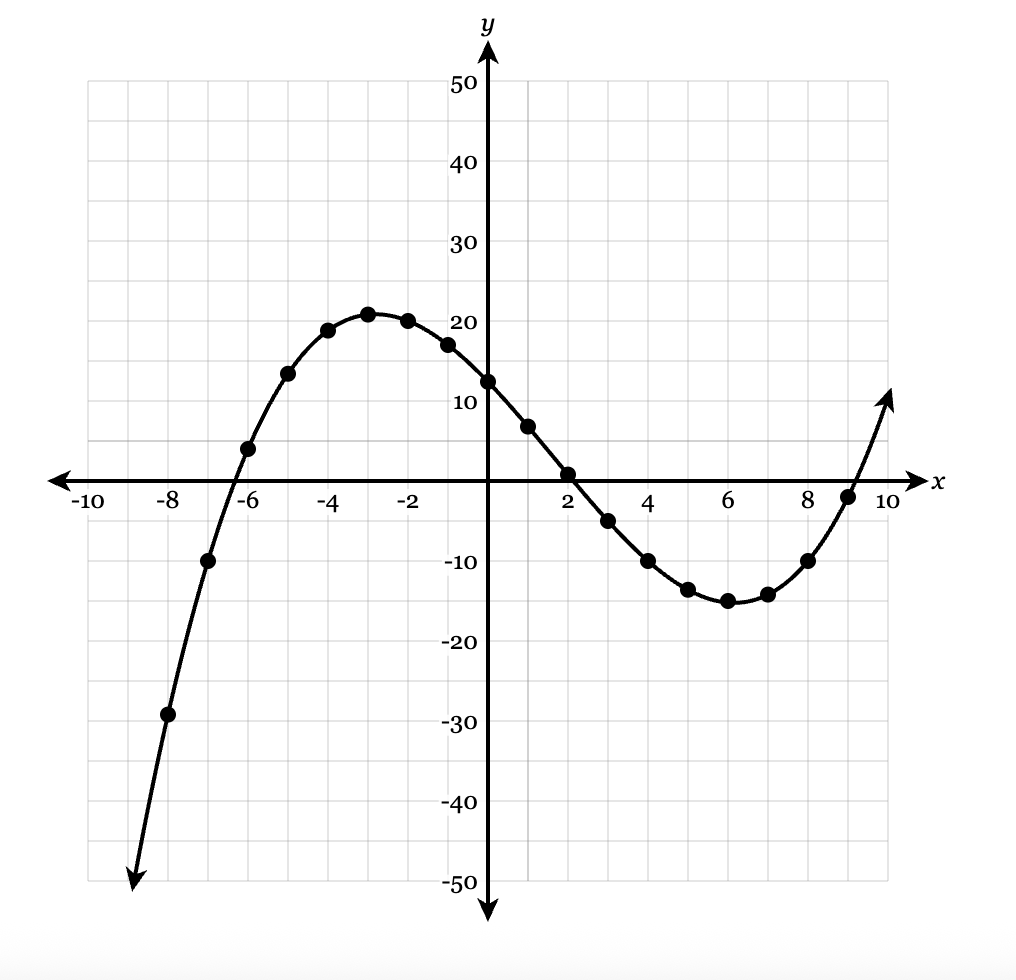
-35/8
300
The three separate transformations that change f(x) to g(x)=−2f(x+3).
1. reflection over x-axis
2. vertical stretch by a factor of 2
3. sift 3 units to the left
300
Jim is taking batting practice. The height in feet of his first hit is shown in the table. The height of his second hit is shown on the graph. What is the approximate difference in the max heights?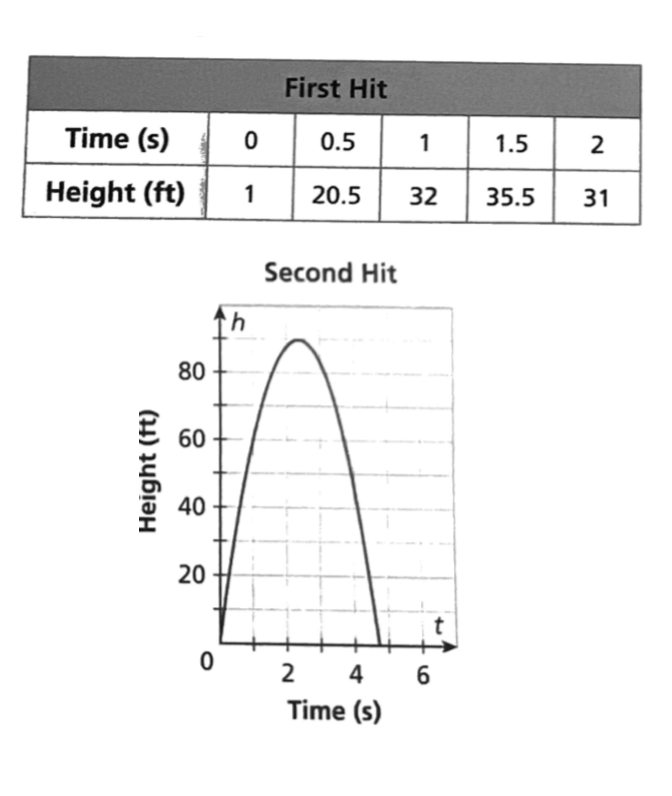
55 ft
400
The range of the function f(x)=x^2+1.
R: [1, ∞)
400
Determine the domain on which this function is decreasing.
(3, 10)
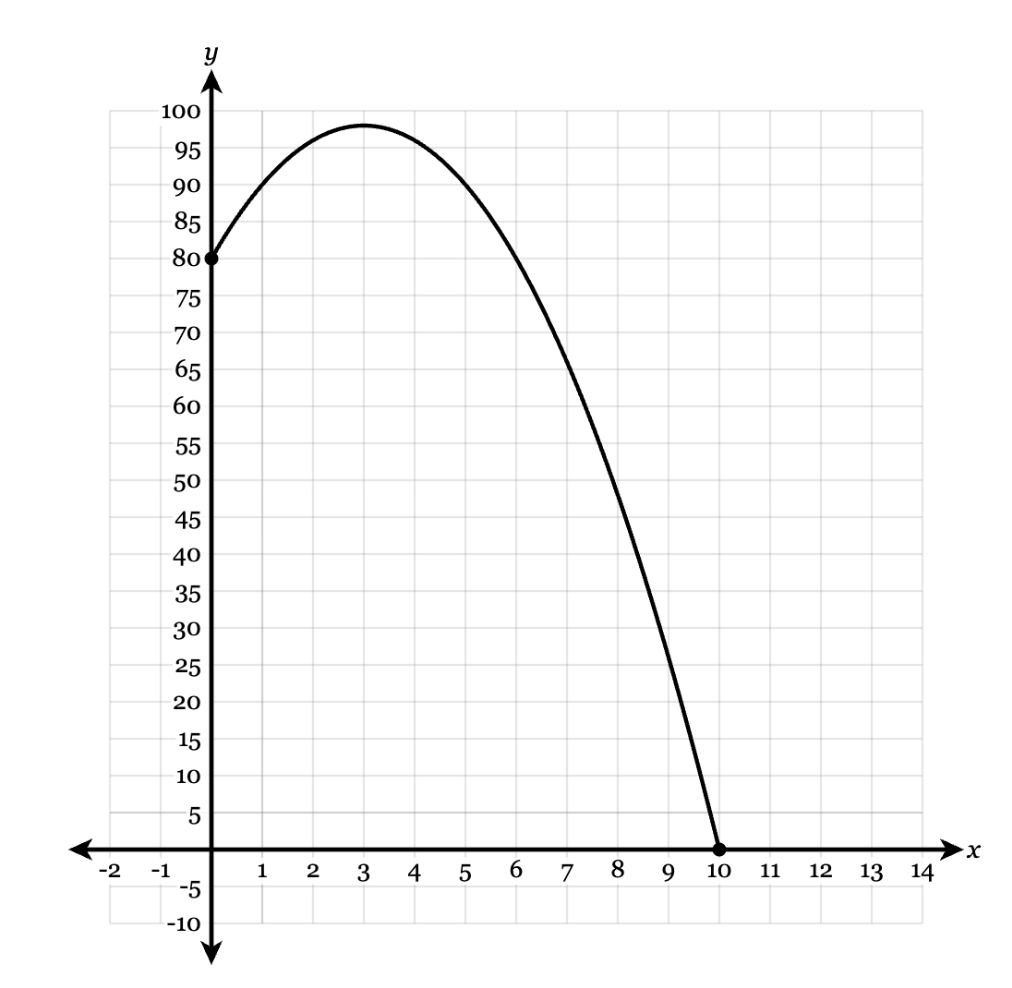
400
Examine the following graph. It represents a journey made by a large delivery truck on a particular day. During the day, the truck made two deliveries, each one taking one hour. The driver also took a one-hour break for lunch. What is the average rate of change from hour 1 to hour 5?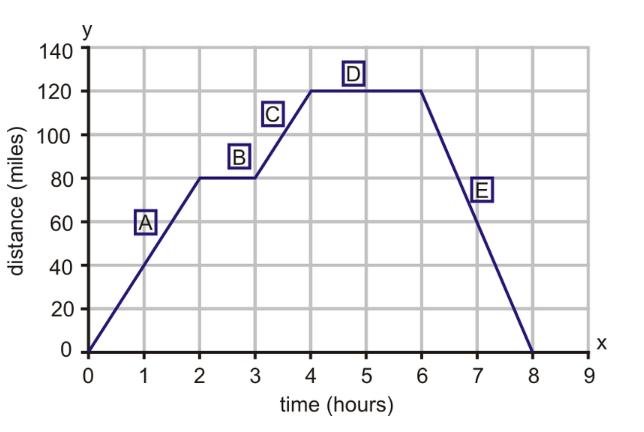
20 mi / hr
400
Find the image of the point (2, 2) on the graph given the indicated transformation.
g(x) = 3/2f(x) - 2
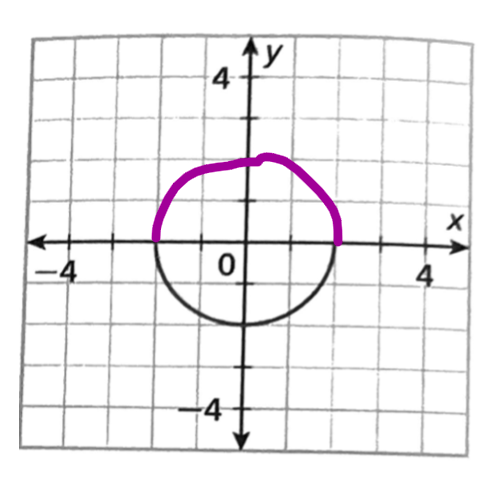
(2, 1)
400
Determine the max value of the function. Round to the nearest integer.
f(t) = −4.9t^2+24.5t+8
39
500
Given f(x) = 4x^2 + 9x + 9, find f(-1).
f(-1) = 4
500
The end behavior of this function.
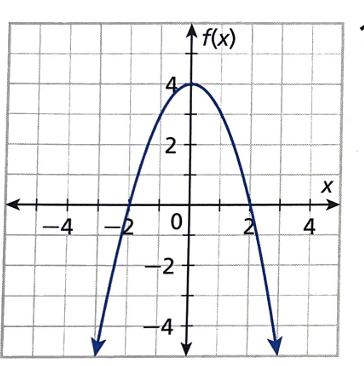
as x -> -∞, f(x) -> -∞
as x -> ∞, f(x) -> -∞
500
Find the average rate of change for the function f(x)=3x−1 on the interval [−1,2].
The rate of change is 3.
500
Find the image of the point (4, -2) given the transformation g(x) = -1/2f(x + 1) + 1
(3, 2)
500
Determine the max height of the function.
A(l) = -2l^2 + 80l
800