Transformations
Inverse Functions
Cubic Functions
Graphing Polynomials
Definitions
100
Define the parameters a, b, h, and k for the cubic function.
a- vertical stretch/compression
b- horizontal stretch/compression
h- horizontal translation
k- vertical translation
100
Given the set of points {(0,1), (3,2), (5,1)} find the inverse set.
What is, {(1,0), (2,3), (1,5)}.
100
How many x-intercepts do cubic functions have?
only one intercept.
100
What is the degree of the polynomial?
f(x)=x(x+3)2
Three
100
Describe the difference between horizontal shift and vertical shift.
horizontal shifts left and right while vertical shifts up and down.
200
Describe the transformations: h(x)=5(x+1)2
vertical stretch of 5 and shift left 1.
200
What line are inverse functions reflected on?
y=x
200
Where is reference point number 1 always located?
in the middle of the cubic function
200
Is the end behavior of this polynomial the same or opposite. Explain how you know.
g(x)= -x(x-4)(x+2)2
Same end behavior.
200
How can you tell if a polynomial is positive or negative?
the leading coefficient
300
True or false: the function f(x)=-x2+3 displays a reflection on the y-axis and a vertical shift up 3 units.
false
300
Find the inverse function, f-1(x), to the function f(x)=3x-4.
What is, f-1(x)=(x+4)/3.
300
Graph
f(x)=-3(x-1)^3+4
300
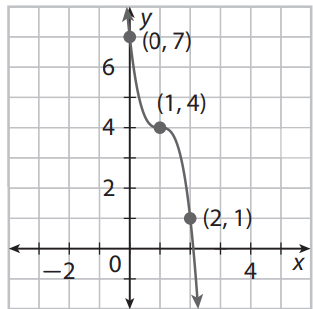
True or false: this polynomial is degree 5.
g(x)= -(x+3)2(x-3)2
false
300
What is the difference between global and local maximum/minimum?
Global is the highest/lowest point for the entire function
Local is the highest/lowest point for a specific section of the function
400
Write an equation for a cubic function that is reflected on the x-axis, vertically stretched by a factor of 4, shifted 7 units right, and shifted 2 units down.
g(x)=-4(x-7)3-2
400
Find the inverse function, f-1(x), to the function
f(x)=3/5x+2
f^-1(x)=5/3x-10/3
400
Write the equation for the graph
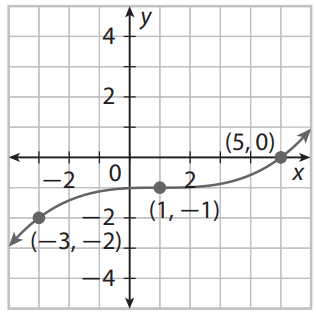
f(x)= (1/4(x-1))^3-1
400
List the x-intercepts for this polynomial. Determine if they cross, are tangent, or bend.
h(x)=x^3(x+5)
Bends at x=0, Crosses at x=-5
400
Define the symmetry for an odd function.
Symmetric through the origin.
500
Write an equation for a cubic function that is horizontally stretched by a factor of 4 and shifted three units left.
g(x)=(1/4(x+3))^3
500
Find the inverse of
f(x)=(x+3)^2-2
f^-1(x)=-3+-sqrt(x+2)
500
Write the equation for the graph
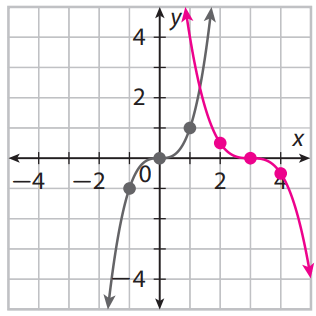
g(x)=-1/2(x-3)^3
500
Determine if the graph is tangent, bends, or crosses at each intercept.
f(x)=x2(x+4)(x-3)2
tangent at 0, cross at -4, tangent at 3.
500
What is the difference between vertical stretch and vertical compression?
vertical stretch when a>1 or a<-1 and vertical compression when -1<a<1.