Determine the algebraic equation that would represent the following:
Seven times a number subtracted from 5 is 26
Expand and simplify
(3x-1)(2x+10)
6x^2+28x-10
What is the y-intercept of the function
y=3x^2-4x-10
(0,-10)
What is the quadratic formula?
x=(-b+-sqrt(b^2-4ac))/(2a)
Determine the value of x if
sinx=0.82
55 degrees
Determine the coordinates of the midpoint Q(-3,-3) and R(-1,-7)
Solve by substitution.
x+4y=6
2x-3y=1
(2, 1)
Expand and simplify.
(x-5)^2-3(2x+7)
x^2-16x+4
State the transformations of
y=-1/2(x-2)^2+8
reflection in the x-axis
vertical compression by a factor of 1/2
horizontal shift right 2 units
vertical shift up 8 units
Solve by factoring.
3x^2-9x
x=0, x=3
ABC is a right triangle.
AB=7cm, angle B is 90 degrees, angle C is 64 degrees. Calculate the length of BC.
3.4 cm
14.6
Solve using elimination
3x+2y=2
4x+5y=12
(-2,4)
What is the GCF of the following?
5x^2y^3-15x^2y^2+45xy^2+20xy
5xy
State the vertex, direction of opening, axis of symmetry and max/min value of the following:
y=8(x-3)^2-7
V=(3,-7)
opens up
x=3
min of -7
Determine the x-intercepts.
2x^2-x-6
(2,0), (-3/2,0)
Find the value of x. Round to one decimal.
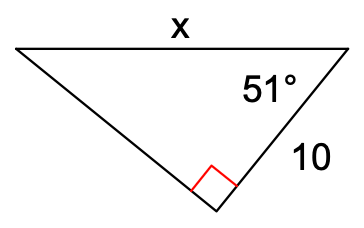
x=15.9
For the triangle with vertices A(-2, 0), B(8, 8) and C(4, -2)
Determine the equation of the median from vertex A
y=3/8x+3/4
Maria had $10 000. She invested part of it in an account paying 4% per annum and remainder in bonds paying 5% per annum. If the total interest earned after 1 year was 440, how much did she invest in each account?
Factor.
x^2-7x+10
(x-5)(x-2)
Find the equation of a parabola that has a vertex at (-2,-5) and goes through the point (0,-3)
y=1/2(x+2)^2-5
Solve using quadratic formula.
(x-2)^2+10=0
x=5.16, x=-1.16
Determine the value of a
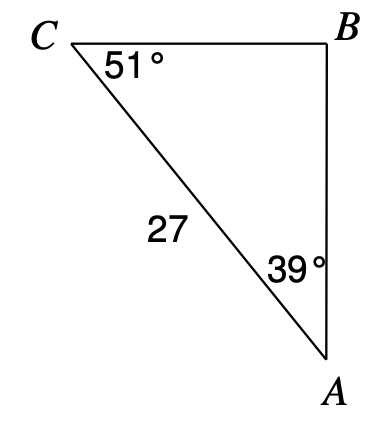
a=17
A triangle has vertices L(8,8), M(-2,0), and N(4,-2)
Determine the equation of the altitude from vertex M.
y=-2/5x-4/5
Maryam would mix 100 mL of the 5% acetic acid with 150 mL of the 10% acetic acid.
Factor.
-12n^2+27m^2
-3(2n+3m)(2n-3m)
Determine the vertex of the parabola.
y=-5x^2+20x+2
V=(2,22)
A sporting goods store sells 90 ski jackets in a season for $200 each. Each $10 decrease in the price would result in five more jackets being sold. What is the max revenue?
The max revenue is $18050
From the hay loft door, Ted sees his dog on the ground. The angle of depression of the dog is 40º. Ted's eye level is 16 feet above the ground. How many feet must the dog walk to reach the open barn door directly below Ted (to the nearest foot)?
19 feet
Determine the equation for the right bisector of the line segment with endpoints P(-5,-2) and Q(3,6)
y=-x+1