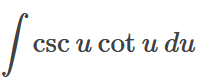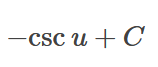U-sub/Density
Area between Curves/Volumes by Cross Section
Disk/Washer/Shell
Arc Length
Parametrics
Antiderivatives
100
Identify 'u'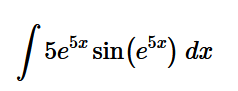 
u = e5x
100
The formula used to find the area between two curves.
What is
A = int_a^b [f(x)-g(x)] dx
Upper - Lower (x bounds)
Right - Left (y bounds)
100
The formulas used to find volumes using Disk & Washer Method (rotated about x-axis).
What is (disk)
V=piint_a^b[f(x)]^2dx
& (washer)
V=piint_a^b[f(x)]^2-[g(x)]^2dx
100
The formula used to find Arc Length.
What is
S=int_a^bsqrt([x'(t)]^2+[y'(t)]^2) dt
100
Sketch the path of the following parametrization:
100
Find the antiderivative:
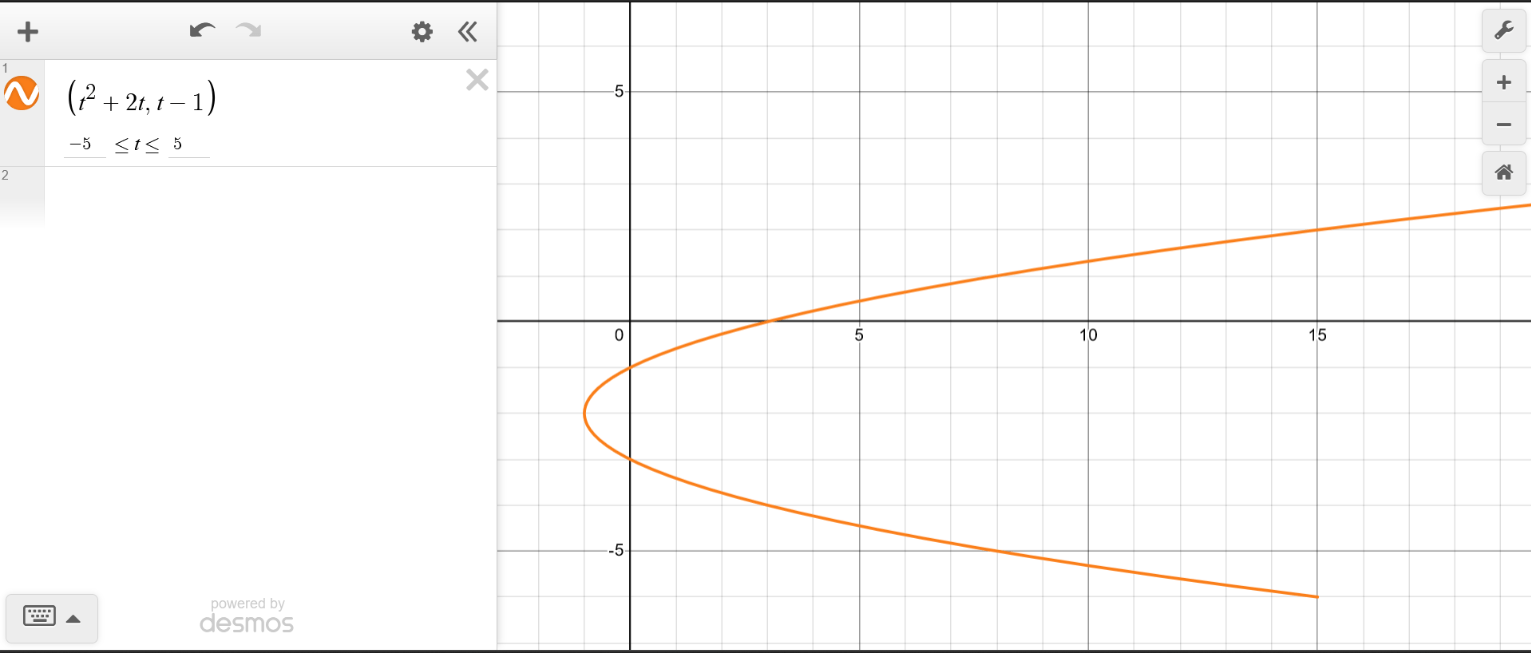
x2
1/3(x3)+C
200
The formula for linear & radial density
What is (Linear)
M=int_a^b p(x) dx
& (Radial)
P=2pi int_0^R r*p(x) dx
200
The formula used to find Volumes by Cross-Sectional Areas.
What is (perp. to x-axis):
V = int_a^bA(x)dx
& (perp. to y-axis):
V = int_c^dA(y)dy
200
The formula used to find a volume of revolution using Shell Method (rotated about y-axis)?
What is
V=2piint_a^bxf(x)dx
200
DOUBLE JEOPARDY:
200
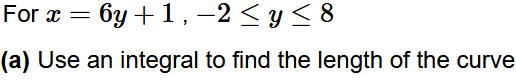
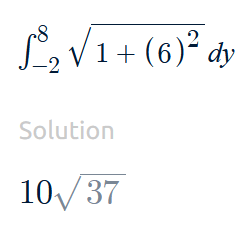
Eliminate the parameter.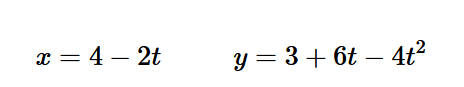
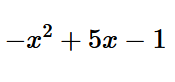
200
Find the antiderivative:
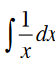
ln(x) + C
300
Setup, but do not evaluate, an integral that represents density.
int 1+cos(pix) dx
300
Set up, DON'T evaluate: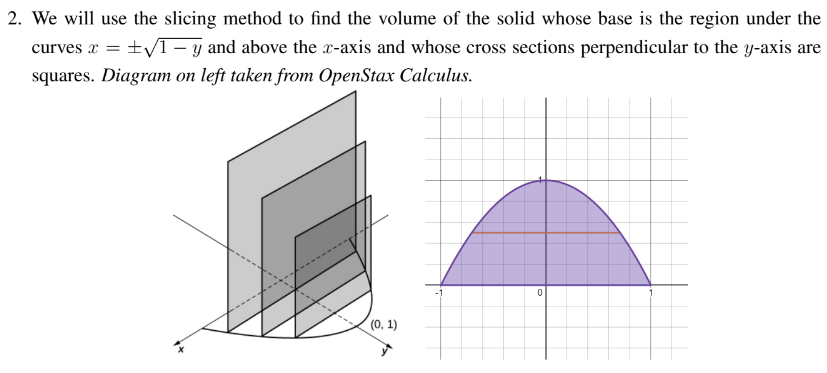
4*int_0^1(1-y)dy
300
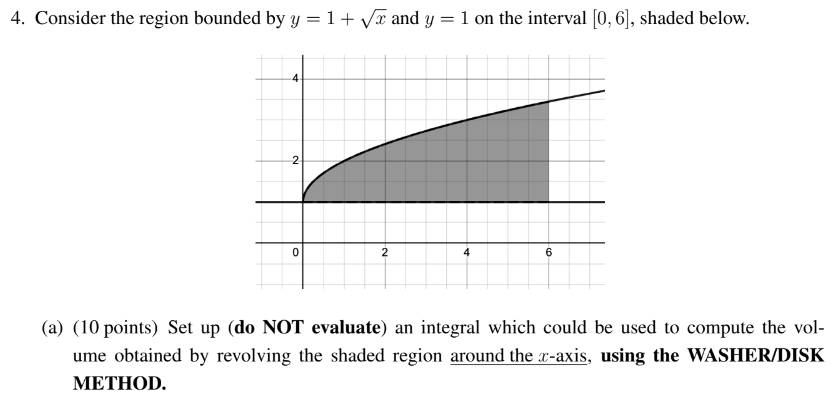
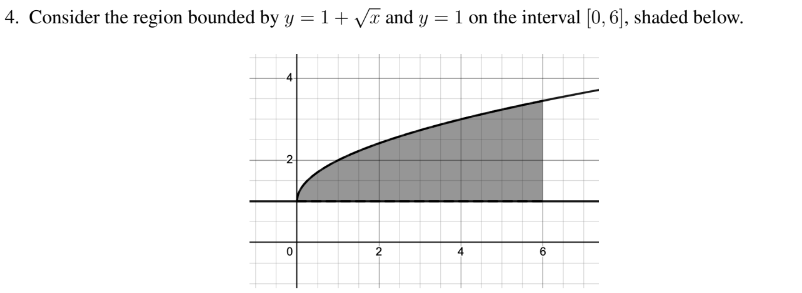
piint_0^6 (1 + sqrtx)^2 - 1 dx
300
Set up, but do NOT evaluate.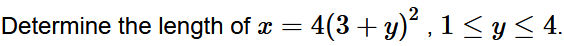
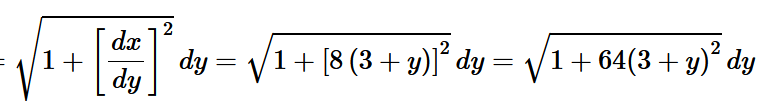
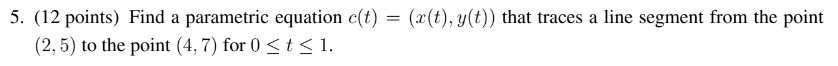
300
x(t) = 2+2t
y(t) = 5+2t
300
Find the antiderivative: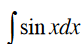 
-cos(x) + C
400
2pi int_1^4 r(60e^(-r^2))dr
400
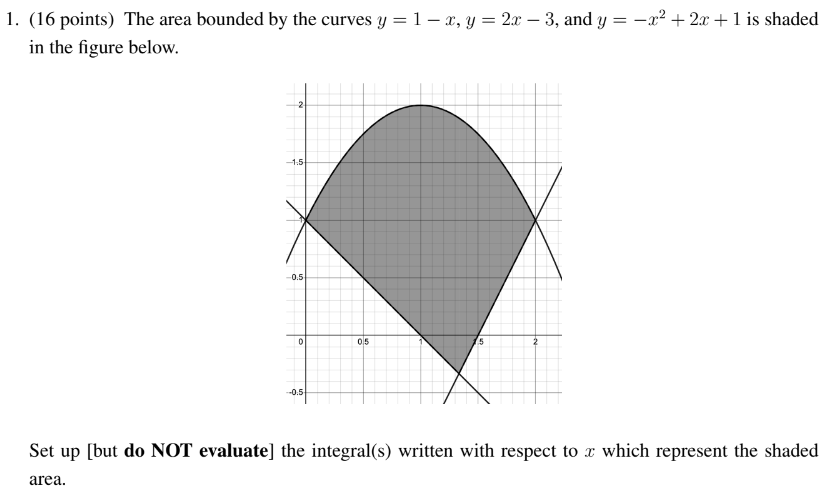
int_0^(4/3) (-x^2+3x)dx + int_(4/3)^2 (-x^2+4)dx
400
2piint_1^(1+sqrt6)y(6-(y-1)^2)dy
400
Set up, do NOT evaluate.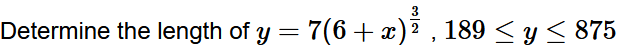
400
Set up, but do not evaluate.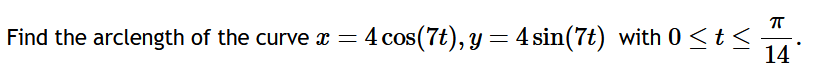
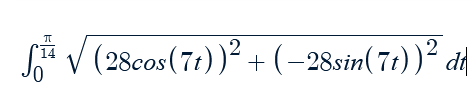
400
Find the antiderivative:
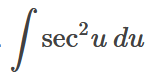
tan(u)+C
500
Evaluate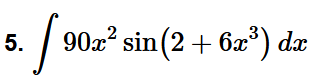 
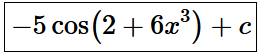
500
Set up, DON'T evaluate: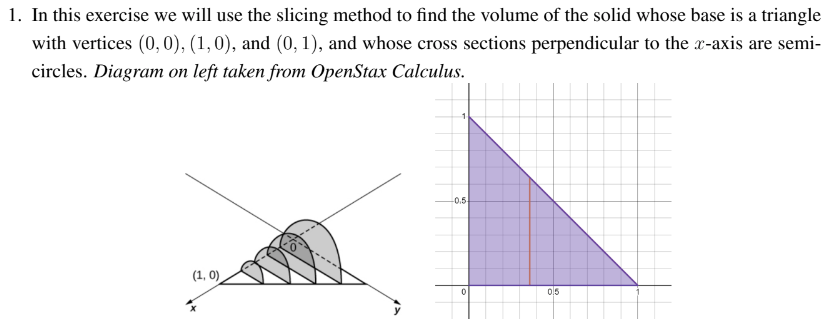
pi/8 int_0^1 (1-x)^2dx
500
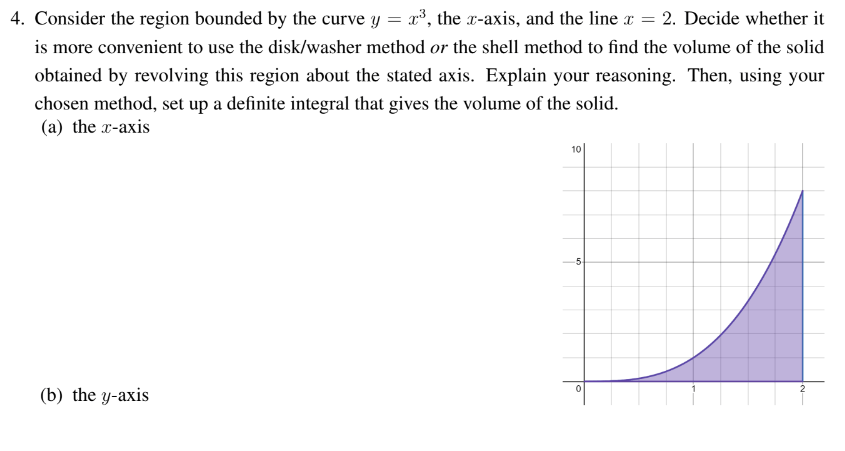
a)
piint_0^2x^6dx
b)
piint_0^(8)4-y^(2/3)dy
or
2piint_0^2x^4dx
500
Set up, DON'T evaluate
(ds)/dt=int_0^1 (sqrt(9+1/4t) )dt
500
~ 34.3 cm
500
Find the antiderivative:
