Riley travels from X to Y for 125 km on a bearing of N32°W. How far did Riley travel due north, to the nearest kilometre?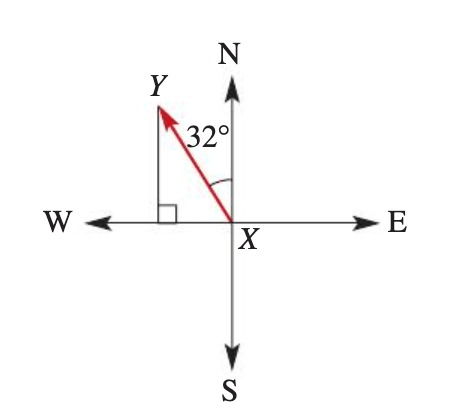
106 km
In triangle ABC, side a is 36 cm, side b is 48 cm and angle C is 68°. Find the area of the triangle. Answer correct to two decimal places.
801.09 cm^2
Benjamin is planning to build a triangular garden for his daughter. The vertices of the triangle are named PQR. He measured =PQ as 2.7 m, QR as 3.1 m and ∠PRQ as 57°. Use the sine rule to find the size of ∠RPQ, correct to the nearest degree.
74
 Ruby drives a four-wheel drive along a track from point A due west to a point B, a distance of 14 km. She then turns and travels 19 km to point C. Use the cosine rule to calculate the distance Ruby is from her starting point. Answer correct to one decimal place.
Ruby drives a four-wheel drive along a track from point A due west to a point B, a distance of 14 km. She then turns and travels 19 km to point C. Use the cosine rule to calculate the distance Ruby is from her starting point. Answer correct to one decimal place.
26 km
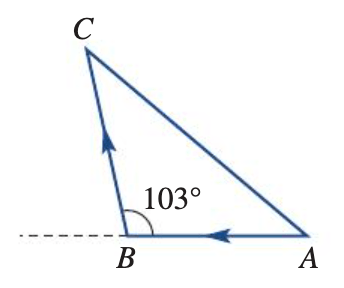
A radial survey of land DEFG. What is the size of angle FOG? 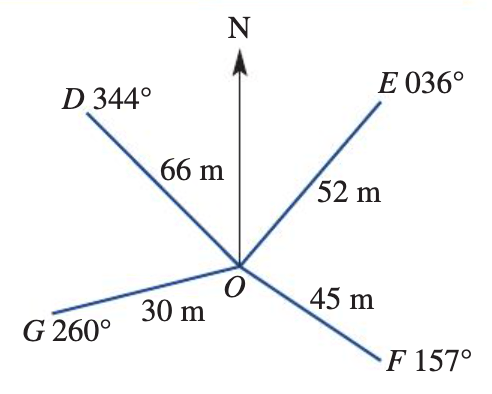 is shown opposite.
is shown opposite.
103
Harry travelled for 8.5 km on a bearing of S30°W from his home. How far west is Harry from home? Answer correct to two decimal places.
4.25 km
Find the area of triangle 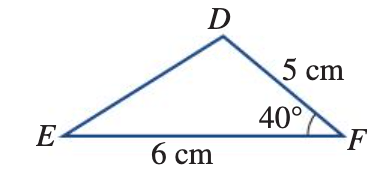 DEF if DF = 5cm, EF = 6cm and ∠DFE = 40°. Answer correct to the nearest square centimetre.
DEF if DF = 5cm, EF = 6cm and ∠DFE = 40°. Answer correct to the nearest square centimetre.
10 cm^2
Find the length of the longest side of a triangle with angles of 42°, 55° and 83°, given that the length of the shortest side is 8.6 cm. Answer correct to one decimal place.
12.8 cm
DEF is a triangle for which DF = 37 cm, EF = 46 cm and ∠DFE = 44°. Use the cosine rule to find the length of DE, to the nearest millimetre.
322 mm
The diagram opposite is a compass radial survey of field VWXYZ. All distances are in metres. Answer the following questions, correct to one decimal place.  What is the length of XY?
What is the length of XY?
68 m
A cyclist rides 15 km on a bearing of 290°. How far north is the cyclist? Answer correct to one decimal place.
5.1km
In triangle 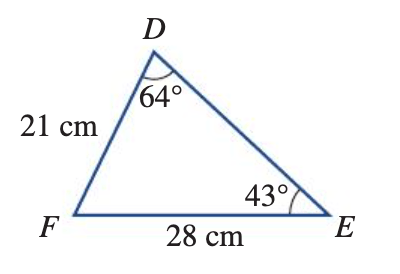 DEF, the length of DF is 21 cm, EF is 28 cm, ∠FDE is 64°and ∠DEF is 43°. Find the area of triangle DEF to the nearest square centimetre.
DEF, the length of DF is 21 cm, EF is 28 cm, ∠FDE is 64°and ∠DEF is 43°. Find the area of triangle DEF to the nearest square centimetre.
281 cm^2
Sienna was located at X and saw a fire in the direction N15°E. Seven kilometres to the east of X at Z, Dylan saw the fire in the direction N50°W. How far is X from the fire? Answer in kilometres, correct to 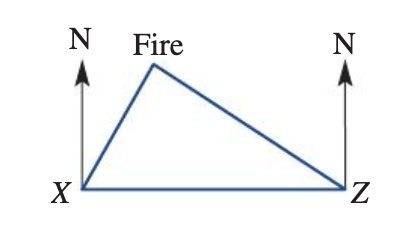 one decimal place
one decimal place
5 km
Passengers in a car travelling east, along a road that runs west–east, see a castle 10 km away in the direction N65°E. When they have travelled a further 4 km east along the road, what will be the distance to the castle? Answer correct to two decimal places.
6.6 km
A radial survey of land ABCD is shown opposite. Answer the 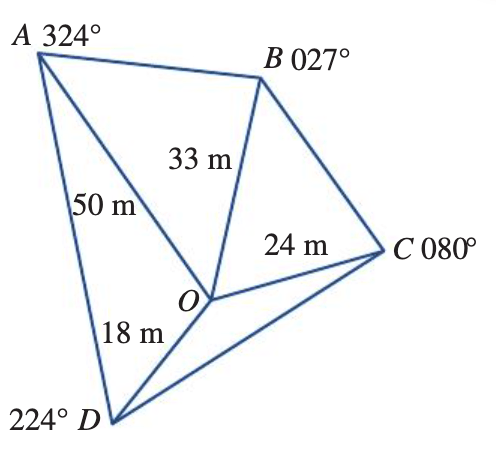 following questions correct to the nearest metre. What is the area of ΔAOB?
following questions correct to the nearest metre. What is the area of ΔAOB?
735 m^2
The diagram shows the location of three schools. School A is 5 km due north of school B, school C is 13 km from school B and ∠ABC is 135°. Calculate the shortest distance from school A to school C, to the nearest kilometre.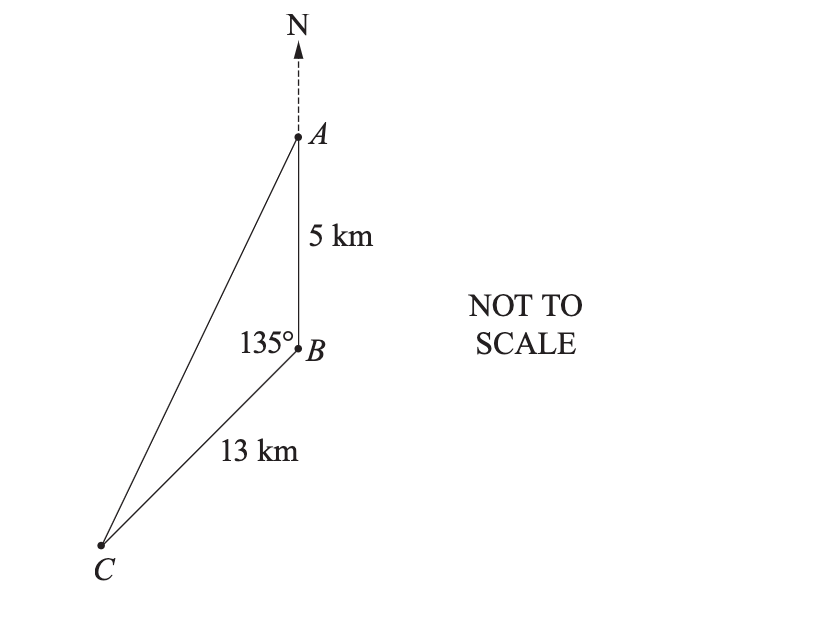
17 km
The triangle  ABC has an area of 243 m2, BC = 30.1 m and ∠BCA = 54°21′. What is the length of AC in metres, correct to one decimal place?
ABC has an area of 243 m2, BC = 30.1 m and ∠BCA = 54°21′. What is the length of AC in metres, correct to one decimal place?
19.9 m
The diagram shows a triangle with side lengths 25 cm and 47 cm and angle 30° and θ. Find θ given it is an obtuse angle. Give your answer to the nearest minute. 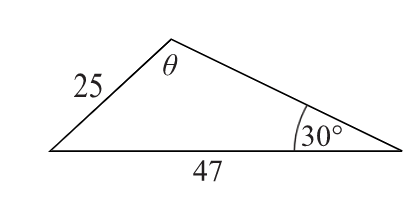
109'57'
A stepladder has legs of length 120 cm and the angle between them is 15°. Calculate the distance (to the nearest centimetre) between the legs on the ground.
31 cm
A radial survey of a triangular field is shown. 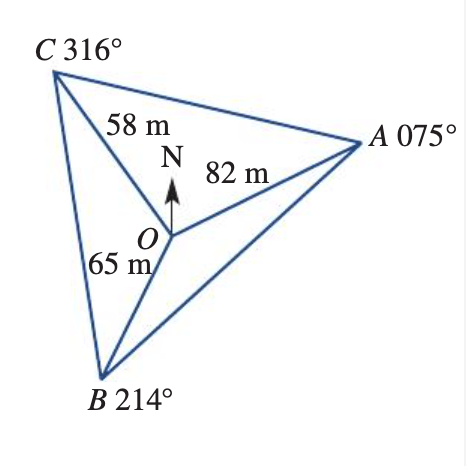 What is the size of ∠AOB?
What is the size of ∠AOB?
139
Oscar drives at a speed of 80 km/h on a bearing of 125°T for 2.5 hours. How far is Oscar east of his starting position? Answer to the nearest kilometre.
164 km
A triangle has an angle of 129°56′with one arm of this angle 15 cm long. What is the length of the other arm of this angle if the area of the triangle is 69.94 cm2? Answer correct to the nearest centimetre.
12 cm
Harrison measured the angle of elevation to the top of the mountain as 28°. He moved 140 m closer to the mountain and measured the angle of elevation to the top of the mountain as 43°. How far in a straight line is Harrison from the top of the mountain at his new position? Answer correct to the nearest metre.
254 m
The lengths of the sides of triangle ABC are in the ratio 7 : 8 : 9. Find the size of each angle, correct to the nearest minute.
74'24', 58'25', 48'11'
Alex, Blake and Connor are standing in a field. Connor (C) is 15 metres away from Blake (B) on a bearing of 032°. Alex (A) is 20 metres away from Blake on a bearing of 315°.
What is the size of the ∠ABC to the nearest degree?
77