+ - of Functions
X / of Functions
Composite Functions
Inverses
Graphing
100
h(x) = 3x + 3
g(x) = -4x + 1
h(x) + g(x) = ?
-x + 4
100
g(x) = -2x + 1
f(x) = 4x - 4
g(x) * f(x)
-8x2 + 12x - 4
100
g(n) = 3n +2
f(n) = 2n2 + 5
g(f(2)) = ?
41
100
Determine whether the 2 functions are inverses.
f(x) = 3x + 2
g(x)=(x-2)/3
Yes
100
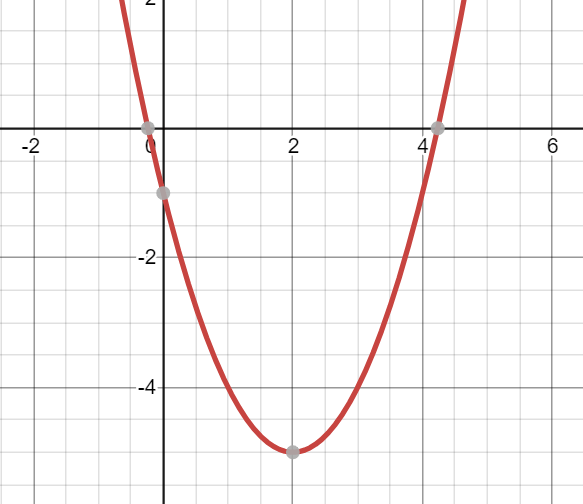
Choose the function that matches the graph.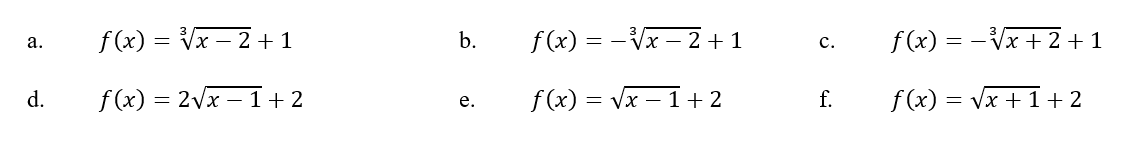
e
200
h(n) = 2n - 1
g(n) = 4n + 5
h(n) + g(n) = ?
6n + 4
200
f(n) = 2n2 + 4
g(n) = -2n + 1
f(x) * g(x)
-2n3 +2n2 - 8n + 4
200
g(t) = t2 + 3
h(t) = 4t - 3
g(h(-1)) = ?
52
200
Determine if the 2 functions are inverses.
f(x) = 2x + 2
g(x) = x - 1
No
200
Choose the equation for the function.
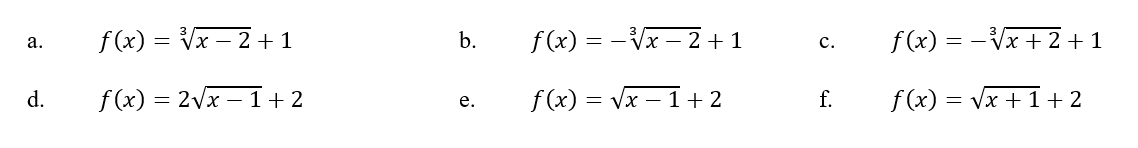
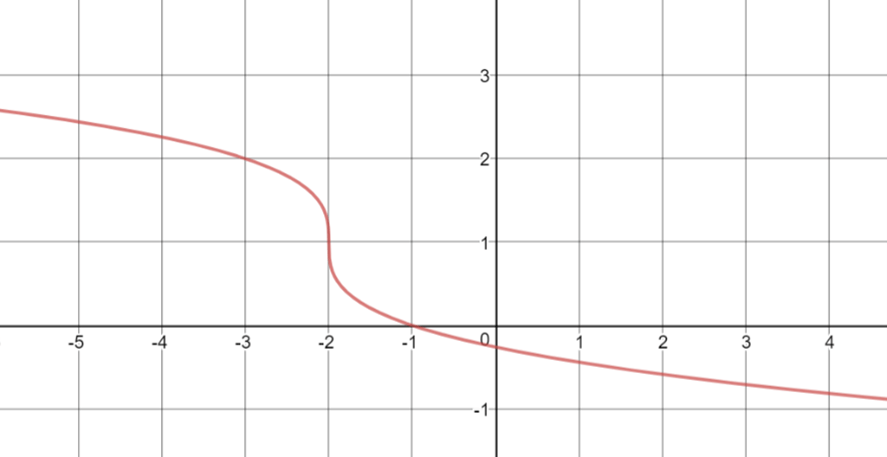
c
300
g(x) = 2x - 2
h(x) = 3x + 2
g(x) - h(x) = ?
-x - 4
300
g(a) = a - 2
h(a) = 2a2 - 4a
(h(a)) / g(a)
2a
300
g(a) = 2a - 1
h(a) = 3a - 3
g(h(-4)) = ?
-31
300
Find the inverse.
f(x) = (3x + 4)/2
f^-1(x)=(2x)/3-4/3
300
Determine whether the inverse is a function. Explain.
No, doesn't pass the Horizontal Line Test.
400
g(a) = 4a - 3
h(a) = 2a - 11
h(a) - g(a) = ?
-2a - 8
400
g(a) = 3a
f(a) = 2a - 4
g(a) * f(a)
6a2 - 12a
400
f(a) = -2a + 3
g(a) = -3a + 4
f(g(a)) = ?
6a - 5
400
Find the inverse.
g(x) = x4 - 3
g^-1(x) = +-root4(x+3)
400
Identify the domain of the function:
f(x) = 3sqrt(x - 2) - 3
[2, oo)
500
f(x) = 4x - 3
g(x) = x3 + 2x
f(x) - g(x) = ?
-x3 + 2x - 3
500
f(n) = 15x6
g(n) = 5x4
f(n)/g(n) = ?
3x2
500
g(x) = 4 - x2
f(x) = x + 2
g(f(x)) = ?
-x2 - 4x
500
Find the inverse:
h(x) = 1/4root3(x)
h^-1(x) = 64x^3
500
Compare to the parent function:
f(x) = 3/4(x + 2)^(1/3) - 1
shift left 2, down 1
Vertical shrink